Relativistic model for anisotropic compact stars in embedding class-I spacetime

Susmita Sarkar; Moumita Sarkar; Nayan Sarkar; Farook Rahaman

doi:10.1088/1572-9494/ad7830

PDF(1128 KB)

Communications in Theoretical Physics ›› 2025, Vol. 77 ›› Issue (1) : 15403. DOI: 10.1088/1572-9494/ad7830

Gravitation Theory, Astrophysics and Cosmology

Relativistic model for anisotropic compact stars in embedding class-I spacetime

Author information +

History +

Abstract

In the present article, we introduce a completely new regular model for static, spherically symmetric celestial fluid spheres in embedding class I spacetime. In this regard, needfully, we propose a new suitable metric potential e^λ(r) to generate the present model. The various analyses on energy density, pressure, anisotropic factor, mass, compactness parameter, redshift, and energy condition make sure the model is physically viable on the ground of model stars Vela X-1, Cen X-3, SMC X-4, and LMC X-4. The reported solutions also respect the equilibrium state by satisfying the Tolman–Oppenheimer–Volkoff (TOV) equation and ensure stability by satisfying the causality condition, condition on the adiabatic index, and Harrison–Zeldovich–Novikov condition. The generated M − R graph matches the ranges of masses and radii for the model compact stars. Additionally, this study provides estimates of the moment of inertia based on the I − M graph.

Key words

general relativity / compact star / anisotropy / Karmarkar condition

Cite this article

EndNote

Ris (Procite)

Bibtex

Download Citations

Susmita Sarkar, Moumita Sarkar, Nayan Sarkar, et al. Relativistic model for anisotropic compact stars in embedding class-I spacetime[J]. Communications in Theoretical Physics, 2025, 77(1): 15403 https://doi.org/10.1088/1572-9494/ad7830

1. Introduction

Research on anisotropic compact stars has consistently remained an area of great interest in relativistic astrophysics after the pioneering work of Bowers and Liang [1]. Several comprehensive studies have elucidated our comprehension of highly dense spherically symmetric fluid spheres characterized by anisotropic pressure [2–5]. The pressure anisotropic can be found inside the celestial compact stars due to the formation of super-fluid neutrons [6], phase transition [7], pion-condensation [8], slow rotation [9], strong magnetic field [10], etc. Dev and Gleiser [11, 12] have explored the influences of pressure anisotropy on the mass, structure and physical properties of compact stars. Böhmer and Harko [13] demonstrated that anisotropic compact objects can exhibit much higher compactness compared to isotropic ones with their radii potentially approaching their corresponding Schwarzschild radii. Chaisi and Maharaj [14] developed an algorithm to find the anisotropic solutions of the field equations for anisotropic matter sources. Anisotropic compact stars have been also studied in the context of general relativity through the analytical approach [15–18] as well as the numerical approach [19–25]. Heintzmann and Hillebrandt [26] proposed a model for a relativistic, anisotropic neutron star at high densities and their analysis revealed that regardless of significant anisotropy, there is no upper limit to the mass of neutron stars. However, they noted that the maximum mass of a neutron star remains beyond 3-4 M_⊙. Sharma et al [27] explored the theoretical feasibility of anisotropy within strange stars, which possess densities surpassing those of neutron stars yet falling short of black holes' densities. Alcock et al [28] and Haensel et al [29] introduced a comprehensive model for compact stars not composed of neutron matter, but characterized by exceedingly high densities within their interiors.

The maximum mass can be controlled by the brane tension λ which lies in the range 3.89 × 10³⁶( ≡ 1.44M_⊙) <λ < 10³⁸dyne/cm² concerning the equation of state (EoS). It is crucial to keep in mind that constructing exact interior solutions for non-uniform stellar configurations in the context of the braneworld is an exceedingly challenging task because of the nonlocality and non-closure of the braneworld equations [30]. The criteria for determining the restrictions needed on braneworld equations to achieve a closed system are still awaiting discovery [31]. To tackle this issue, it is essential to grasp the bulk geometry and comprehend how a 4-dimensional spacetime can be embedded. Castro et al [32] used the concept of embedding 4-dimensional spacetime in 5-dimensional hyperspace to embed a four-dimensional spacetime into a 5-dimensional braneworld. For the first time, Karmarkar [33] introduced a condition for embedding 4-dimensional spacetime into 5-dimensional Euclidean space in terms of the components of Riemannian curvature tensor, known as the embedding class-I spacetime. Randall–Sundrum model [34] is also based on our 4-dimensional spacetime being a hypersurface embedded into another 5-dimensional hypersurface in string theory. Ivanov [35] recently derived a condition akin to the Karmarkar condition for conformally flat spacetime. It is observed that the solutions arising from the two theories are entirely distinct. There are no physical solutions describing isotropic fluid distributions in the Karmarkar spacetime, i.e. class-I spacetime. However, viable physical solutions emerge when incorporating electric charge, anisotropy, or both [36–56].

In general relativity, an n-dimensional spacetime is classified as class-p if it is embedded in (n + p)-dimensional Pseudo Euclidean flat space. According to Kasner [56], the 4-dimensional spacetime of a spherically symmetric matter distribution can always be embedded in 6-dimensional Pseudo Euclidian space, which was also verified by Gupta and Goyel [57]. Eddington [58] discovered that an n-dimensional spacetime can always be embedded in k-dimensional Pseudo Euclidean space, where k = n(n + 1)/2 and the required minimum extra dimension to embedded is less than or equal to the number (k − n) or same as n(n − 1)/2. Particularly, the Schwarzschild interior solution is of class-I, the Schwarzschild exterior solution is of class-II, Friedman–Robertson–Lemaitre spacetime is of class-I [59–61] and the Kerr metric is of class-V [62].

In this article, we have introduced a new model for static, spherically symmetric anisotropic compact stars in the framework of embedding class-I spacetime based on the model compact stars, Vela X-1, Cen X-3, SMC X-4, and LMC X-4. Vela X-1 is a quintessential example of a high-mass x-ray binary (HMXB), comprising a neutron star orbiting closely around the 23.5 M_⊙ B0.5 Ib supergiant donor star HD 77 581. The rocket-borne experiment [63] and the Uhuru satellite observations [64] revealed the matter source was extremely variable. The comprehensive study of Vela X-1 is done in [65]. In 1967, the rocket-borne detector [63] discovered the compact star Cen X-3, which is the most luminous x-ray pulsar in our galaxy. Later, Giacconi et al [66] and Schreier et al [67] identified the binary and pulsar characteristics of Cen X-3 through satellite observations. Price et al [68] detected the compact star SMC X-4 residing in the Small Magellanic Cloud and it has significant variability in both the intensity and spectrum [69]. Schreier et al [70] reported the binary nature of SMC X-4 and discovered periodic occultations with an orbital period of around 3.9 days. For the first time, the compact star LMC X-4 was detected by the Uhuru satellite observations [64] in 1972. Later, Chevalier and Ilovaisky [71] revealed the binary nature of its optical counterpart.

The following article is structured as follows. We have formulated the Einstein field equations for static and spherically symmetric matter distribution in section 2. Section 3 describes the Embedding Class-I spacetime that meets the Karmarkar condition. We have introduced new class-I solutions along with mass, compactness parameter, surface redshift and gravitational redshift in section 4. Section 5 deals with the physical acceptance of the reported solutions. The matching condition of our internal solutions with the exterior Schwarzchild solution are analyzed section 6. We have analyzed the equilibrium and stability of the present model sections 7 and 8, respectively. The generating functions for our model have been computed in section 9. Section 10 describes the moment of inertia and mass relationship. Finally, the results and discussions have been conducted in section 11.

2. Einstein's field equations

To present the pertinent equations for characterizing a static, spherically symmetric self-gravitating locally bounded anisotropic fluids we consider the line element in Schwarzschild coordinate system (t, r, θ, φ) as [72]

\begin{array}{rcl} d s^{2} = - e^{ν (r)} {d t}^{2} + e^{λ (r)} d r^{2} + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}), \end{array}

(1)

where, e^ν(r) and e^λ(r) are functions dependent solely on the radial coordinate r, referred to as metric potential functions. The energy-momentum tensor for the anisotropic fluid sphere can be expressed in the following form

\begin{array}{rcl} \begin{array}{rcl} T_{α β} & = & {P_{r} (r) - P_{t} (r)} χ_{α} χ_{β} \\ + {ρ (r) + P_{t} (r)} U_{α} U_{β} - P_{t} (r) g_{α β}, \end{array} \end{array}

(2)

where, ρ(r), P_r(r), and P_t(r) denote the energy density, radial pressure, and transverse pressure of the matter configuration, respectively. U^α is the four-velocity given by U^α = (e^−ν(r)/2, 0, 0, 0) and χ^α is the unit space-like vector given by χ^α = (0, e^−λ(r)/2, 0, 0), satisfying U^αU_α = − χ^αχ_α = 1, U^μχ_μ = 0. It is noted that

\begin{array}{rcl} T_{0}^{0} = ρ (r), T_{1}^{1} = - P_{r} (r), T_{2}^{2} = T_{3}^{3} - P_{t} (r) . \end{array}

(3)

The above interpretation is clear and definite in the case of static, spherically symmetric self-gravitating anisotropic fluid sphere [73].

Now, the Einstein field equations for the line element (1) with the energy-momentum tensor (3) can be written as (taking gravitational unit G = c = 1)

\begin{array}{rcl} ρ (r) = \frac{1}{8 π} {\frac{1 - e^{- λ (r)}}{r^{2}} + \frac{λ^{'} (r) e^{- λ (r)}}{r}}, \end{array}

(4)

\begin{array}{rcl} P_{r} (r) = \frac{1}{8 π} {\frac{ν^{'} (r) e^{- λ (r)}}{r} - \frac{1 - e^{- λ (r)}}{r^{2}}}, \end{array}

(5)

\begin{array}{rcl} \begin{array}{rcl} P_{t} (r) & = & \frac{e^{- λ (r)}}{32 π} {2 ν^{''} (r) + {ν^{'} (r)}^{2} - ν^{'} (r) λ^{'} (r) \\ + \frac{2 ν^{'} (r)}{r} - \frac{2 λ^{'} (r)}{r}} . \end{array} \end{array}

(6)

where, ‘′' stands for the derivative with respect to the radial coordinate r.

The anisotropic factor for static and spherically symmetric fluid configuration is characterized as Δ(r) = P_t(r) −P_r(r) [74], therefore, one can get the expression for Δ(r) from equations (5)–(6) as

\begin{array}{rcl} \begin{array}{rcl} Δ (r) & = & \frac{e^{- λ (r)}}{8 π} {\frac{ν^{''} (r)}{2} - \frac{λ^{'} (r) ν^{'} (r)}{4} + \frac{{ν^{'} (r)}^{2}}{4} \\ - \frac{ν^{'} (r) + λ^{'} (r)}{2 r} + \frac{e^{λ} (r) - 1}{r^{2}}} . \end{array} \end{array}

(7)

Now, overall, we possess three field equations (4)–(6) for five unknown functions: e^ν(r), e^λ(r), ρ(r), P_r(r), and P_t(r), therefore, we can freely select two of them so that the model becomes physically realistic.

3. The Karmarkar condition

In the study of stellar fluid configurations, the Karmarkar condition has a convenient effect because it creates a beautiful relationship between two metric potentials. In 1948, Karmarkar established a condition for embedding class-I spacetime in terms of the components of Riemannian curvature tensor R_αβγδ as [33]

\begin{array}{rcl} R_{1414} R_{2323} = R_{1212} R_{3434} + R_{1224} R_{1334} . \end{array}

(8)

The above condition is known as the Karmarkar condition, and by satisfying this, a 4-dimensional spacetime can be embedded in 5-dimensional flat space, i.e. becomes embedded in class-I spacetime. It is noted that the Karmarkar condition acts as the necessary condition only, Pandey and Sharma [75] derived the sufficient condition as R₂₃₂₃ ≠ 0.

For the line element (1), the non-zero components of Riemannian curvature tensor R_αβγδ are

\begin{array}{rcl} \begin{array}{rcl} R_{1212} & = & \frac{r}{2} λ^{'} (r), R_{2424} = \frac{r}{2} ν^{'} (r) e^{ν (r) - λ (r)}, \\ R_{2323} & = & r^{2} \sin^{2} θ [1 - e^{- λ (r)}], \end{array} \end{array}

(9)

\begin{array}{rcl} \begin{array}{rcl} R_{3434} & = & \frac{r}{2} ν^{'} (r) \sin^{2} θ e^{ν (r) - λ (r)}, \\ R_{1414} & = & \frac{e^{ν (r)}}{4} [2 ν^{''} (r) + {ν^{'} (r)}^{2} - ν^{'} (r) λ^{'} (r)] . \end{array} \end{array}

(10)

Considering all these non-zero components of the R_αβγδ, the Karmarkar condition (8) generates the following differential equation

\begin{array}{rcl} 2 ν^{''} (r) + {ν^{'} (r)}^{2} = \frac{e^{λ (r)} ν^{'} (r) λ^{'} (r)}{e^{λ (r)} - 1}, \end{array}

(11)

with e^λ(r)≠1 [75]. Solving the above differential equation (11), we obtain

\begin{array}{rcl} e^{ν (r)} = {A + B \int \sqrt{e^{λ (r)} - 1} d r}^{2} . \end{array}

(12)

where, A and B are non-zero constants of integration, they will be determined from the boundary conditions.

On using equations (11)–(12), the pressure anisotropic (7) reads as [76]

\begin{array}{rcl} Δ (r) = \frac{ν^{'} (r)}{32 π e^{λ (r)}} {\frac{2}{r} - \frac{λ^{'} (r)}{e^{λ (r)} - 1}} {\frac{ν^{'} (r) e^{ν (r)}}{2 {r B}^{2}} - 1} . \end{array}

(13)

It is noted that the pressure anisotropic Δ(r) becomes zero, i.e. it becomes isotropic for the following cases:

•

Case-1: $\frac{λ^{'} (r)}{e^{λ (r)} - 1} = \frac{2}{r}$ : in this case, one can get e^−λ(r) = 1- Cr² with C as an integration constant. Now, the condition (12) yields the other metric potential as $e^{ν (r)} = {(A - B \sqrt{(1 - {C r}^{2}) / C})}^{2}$ . On using e^−λ(r) = 1- Cr² in equation (4) one can see that the energy density becomes constant and this solution is essentially the Schwarzschild interior solution [77].

•

Case-2: $\frac{ν^{'} (r) e^{ν (r)}}{2 {r B}^{2}} = 1$ : in this case, one can obtain e^ν(r)=D + B²r² with D as an integration constant. Similarly, the condition (12) yields e^λ(r)=(D + 2B²r²)/(D + B²r²). This solution yields the Kohlar–Chao solution [78].

Here, we are interested in considering anisotropic pressure, therefore, we shall introduce a new metric potential function to generate the physical model.

4. New solutions via the Karmarkar condition

To formulate the model for anisotropic celestial matter configurations in embedding class-I spacetime, we introduce a completely new metric potential function as

\begin{array}{rcl} e^{λ (r)} = 1 + {a r}^{2} \coth^{2} ({b r}^{2} + c), \end{array}

(14)

where a > 0 (km⁻²), b (km⁻²), and c are constants.

Employing equation (14) in equation (12), we obtain other metric potential as

\begin{array}{rcl} e^{ν (r)} = {[A + \frac{\sqrt{a} B}{2 b} l o g [\sinh ({b r}^{2} + c)]]}^{2} . \end{array}

(15)

Now, considering the above metric potentials (14) and (15) we obtain the fluid parameters ρ(r), P_r(r), P_t(r) and Δ(r) in the following form

\begin{array}{rcl} ρ (r) = \frac{a \coth ({b r}^{2} + c) [3 \coth ({b r}^{2} + c) + {a r}^{2} \coth^{3} ({b r}^{2} + c) - 4 {b r}^{2} {c s c h}^{2} ({b r}^{2} + c)]}{8 π {[1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)]}^{2}}, \end{array}

(16)

\begin{array}{rcl} P_{r} (r) = \frac{\coth ({b r}^{2} + c) [4 \sqrt{a} b B - a \coth ({b r}^{2} + c) (2 A b + \sqrt{a} B l o g [\sinh ({b r}^{2} + c)])]}{8 π [1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)] [2 A b + \sqrt{a} B l o g (\sinh ({b r}^{2} + c))]}, \end{array}

(17)

\begin{array}{rcl} P_{t} (r) = \frac{2 \sqrt{a} b B [{a r}^{2} \coth^{3} ({b r}^{2} + c) + 2 \coth ({b r}^{2} + c) - 2 {b r}^{2} {c s c h}^{2} ({b r}^{2} + c)] - a ξ_{1}}{8 π {[1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)]}^{2} [2 A b + \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]]}, \end{array}

(18)

\begin{array}{rcl} Δ (r) = \frac{\sqrt{a} r^{2} ξ_{2} [\coth ({b r}^{2} + c) {2 \sqrt{a} A b + a B l o g [\sinh ({b r}^{2} + c)]} - 2 b B]}{8 π {[1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)]}^{2} [2 A b + \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]]}, \end{array}

(19)

whereas,

\begin{array}{rcl} \begin{array}{rcl} ξ_{1} & = & \coth ({b r}^{2} + c) [\coth ({b r}^{2} + c) - 2 {b r}^{2} {c s c h}^{2} ({b r}^{2} + c)] \\ \times [2 A b + \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]], \\ ξ_{2} & = & a \coth^{3} ({b r}^{2} + c) + 2 b {c s c h}^{2} ({b r}^{2} + c) . \end{array} \end{array}

(20)

The mass function m(r) and compactness parameter u(r) for the fluid sphere are obtained as [79]

\begin{array}{rcl} \begin{array}{rcl} m (r) & = & \int_{0}^{r} 4 π {\bar{r}}^{2} ρ (\bar{r}) d \bar{r} \\ = & \frac{{a r}^{3} \cosh^{2} ({b r}^{2} + c)}{({a r}^{2} + 1) \cosh [2 ({b r}^{2} + c)] + {a r}^{2} - 1}, \end{array} \end{array}

(21)

\begin{array}{rcl} u (r) = \frac{m (r)}{r} = \frac{{a r}^{2} \cosh^{2} ({b r}^{2} + c)}{({a r}^{2} + 1) \cosh [2 ({b r}^{2} + c)] + {a r}^{2} - 1} . \end{array}

(22)

Also, we obtain the gravitational redshift Z_g(r) and surface redshift Z_s(r) as [79]

\begin{array}{rcl} \begin{array}{rcl} Z_{g} (r) & = & e^{- ν (r) / 2} - 1 \\ = & \frac{2 b}{2 A b + \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]} - 1, \end{array} \end{array}

(23)

\begin{array}{rcl} \begin{array}{rcl} Z_{s} (r) & = & \sqrt{1 - 2 u (r)} - 1 \\ = & {[1 - \frac{2 {a r}^{2} \cosh^{2} ({b r}^{2} + c)}{({a r}^{2} + 1) \cosh [2 ({b r}^{2} + c)] + {a r}^{2} - 1}]}^{1 / 2} - 1. \end{array} \end{array}

(24)

5. Physical characteristics

For any physically viable anisotropic compact stars model, it is imperative to satisfy the following regularity and reality conditions consistently throughout the interior of the stellar configurations.

•	The spacetime must be devoid of singularities, meaning that the metric functions e^λ(r) and e^ν(r) should remain finite and devoid of any singularities.
•	The energy density and radial pressure component ought to be positive and reach their maximum values at the centre while decreasing monotonically towards the boundary of the star. Furthermore, the radial and traversal pressures should be equal at the centre [4], indicating the absence of anisotropy at the centre of the star.
•	The mass function m(r) and compactness parameter u(r) must be positively finite and increasing in nature, also 2u(r) < 8/9, Buchdahl limit [80].
•	The surface redshift should be positively finite and increasing while the gravitational redshift should be positively finite and decreasing in nature.
•	The equation of state parameters for the stellar model must be ∈ (0, 1) [81]. Also, the stellar model needs to satisfy all the energy conditions [82, 83].

In order to properly justify our proposed model, we analyze the solutions graphically for four well-known compact stars, namely Vela X-1, Cen X-3, SMC X-4, and LMC X-4, and obtain the following results.

5.1. Evaluation of physical parameters

The introduced metric potentials e^−λ(r) and e^ν(r), both are finite inside the compact stars (see figure 1 (left)), illustrating the non-singular geometry of the compact stars. Moreover, e^−λ(r) and e^ν(r) are matched with the exterior Schwarzchild solution at the surfaces of the matter configurations as expected. The energy density is positive with the maximum value at the centres and decreases towards the surfaces, clear from figure 1 (right). The radial pressure P_r(r) is positively maximum at the centres and monotonically decreasing toward the surfaces of the stars with the zero values at the surfaces (see figure 2 (left)). The transverse pressure P_t(r) is also maximum at the centres of the stars and monotonically decreasing toward the surfaces of the compact stars Vela X-1 and Cen X-3 while it has slightly decreasing and increasing behaviours for the compact stars SMC X-4 and LMC X-4, clear figure 2 (left). Additionally, P_t(r) = P_r(r) at the centres of the stars and P_t(r) > P_r(r) for 0 < r ≤ R, which creates the positive anisotropy within the fluid configurations with the absence anisotropy at the centres (see figure 2 (right)). The symmetric profiles of energy density, radial pressure, and pressure anisotropic are depicted in figure 3, indicating the same satisfactory scenarios for all of them.

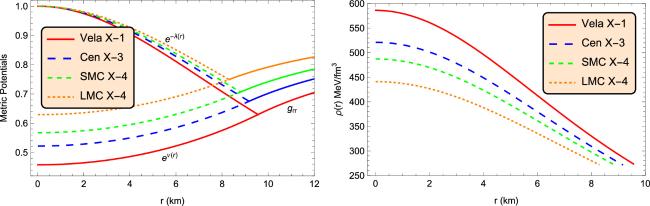
Figure 1. Characteristics of metric potentials (left) and energy density (right) against the radial coordinate r corresponding to the numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

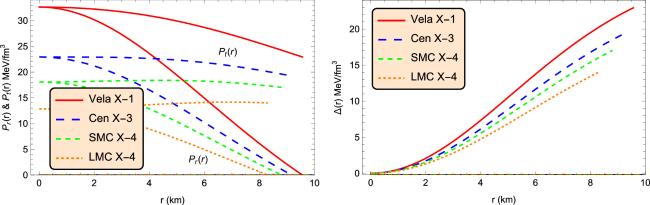
Figure 2. Characteristics of radial and transverse pressures (left) and anisotropic factor (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

Figure 3. Symmetric profiles of energy density (red centres), radial pressure (yellow centres), and anisotropic factor (green centres) corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

Here, we obtain the central density and pressure at the centres of compact stars as

\begin{array}{rcl} ρ_{c} = \frac{3 a}{8 π} \coth^{2} (c), \end{array}

(25)

\begin{array}{rcl} \begin{array}{rcl} P_{r_{c}} & = & P_{t_{c}} \\ = & \frac{\coth (c) [4 \sqrt{a} b B - a \coth (c) {2 A b + \sqrt{a} B l o g [\sinh (c)]}]}{8 π [2 A b + \sqrt{a} B l o g [\sinh (c)]]} . \end{array} \end{array}

(26)

The positive nature of the central pressure,

P_{r_{c}} = P_{t c} > 0

suggests

\begin{array}{rcl} \frac{A}{B} < \frac{4 b - a \coth (c) l o g [\sinh (c)]}{2 \sqrt{a} b \coth (c)} . \end{array}

(27)

Moreover, according to the Zeldovich condition

P_{r_{c}} / ρ_{c} ⩽ 1

[84], we obtain the following inequality

\begin{array}{rcl} \frac{b \tanh (c) - a l o g [\sinh (c)]}{2 \sqrt{a} b} ⩽ \frac{A}{B}, \end{array}

(28)

Therefore, the inequalities (27) and (28) simultaneously read as

\begin{array}{rcl} \begin{array}{l} \frac{b \tanh (c) - a l o g [\sinh (c)]}{2 \sqrt{a} b} \\ ⩽ \frac{A}{B} < \frac{4 b - a \coth (c) l o g (\sinh (c))}{2 \sqrt{a} b \coth (c)} . \end{array} \end{array}

(29)

The above inequality is a boundary constraint on the constants A and B.

Furthermore, the mass function m(r) and compactness parameter u(r) for our proposed solutions are well-defined, zero at the centres of the fluid spheres and then positively increasing in nature within the compact stars with 2u(r) < 8/9, clear from figure 4 (left). Figure 4 (right) illustrates that the surface redshift is positively finite and increasing while the gravitational redshift is positively finite and decreasing in nature within the stars, moreover, at the surfaces (r = R) Z(R) =Z_s(R) = Z_g(R).

Figure 4. Characteristic of mass, compactness parameters (left) and surface, gravitational redshifts (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

5.2. Equation of state parameters

The EoS parameters ω_r(r) and ω_t(r) are dimensionless quantities that create the relationship between energy density and pressure. For our solutions, the EoS parameters ω_r(r) and ω_t(r) are obtained as [85, 86]

\begin{array}{rcl} \begin{array}{rcl} ω_{r} (r) & = & \frac{P_{r} (r)}{ρ (r)} \\ = & \frac{1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)}{a [2 A b + \sqrt{a} B l o g (\sinh ({b r}^{2} + c))]} \\ \times [4 \sqrt{a} b B - a \coth ({b r}^{2} + c) (2 A b + \sqrt{a} B \\ \times l o g [\sinh ({b r}^{2} + c)])] [3 \coth ({b r}^{2} + c) \\ {+ {a r}^{2} \coth^{3} ({b r}^{2} + c) - 4 {b r}^{2} {c s c h}^{2} ({b r}^{2} + c)]}^{- 1}, \end{array} \end{array}

(30)

\begin{array}{rcl} \begin{array}{rcl} ω_{t} (r) & = & \frac{P_{t} (r)}{ρ (r)} \\ = & \frac{2 \sqrt{a} b B [{a r}^{2} \coth^{3} ({b r}^{2} + c) + 2 \coth ({b r}^{2} + c) - 2 {b r}^{2} {c s c h}^{2} ({b r}^{2} + c)] - a ξ_{1}}{a \coth ({b r}^{2} + c) [3 \coth ({b r}^{2} + c) + {a r}^{2} \coth^{3} ({b r}^{2} + c) - 4 {b r}^{2} {c s c h}^{2} ({b r}^{2} + c)]} [2 A b \\ {+ \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]]}^{- 1} . \end{array} \end{array}

(31)

The behaviours of EoS parameters ω_r(r) and ω_t(r) are demonstrated in figure 5 (left), which indicates that both the parameters are within the region 0 < ω_r(r), ω_t(r) < 1 [81], and hence, the present solutions are fit to describe the physical matter configurations.

Figure 5. Characteristic of EoS parameters (left) and ρ(r) + P_r(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

5.3. Energy conditions

The energy conditions are necessary to analyze the matter distribution (normal/exotic) inside the stellar objects. It is a well-established fact that physical mass distributions must adhere to all energy conditions within the matter configurations. The energy conditions, namely (i) null energy condition (NEC), (ii) weak energy condition (WEC) and (iii) strong energy condition (SEC) are defined as [82, 83]

\begin{array}{rcl} \begin{array}{rcl} {N E C}_{r} & : & ρ (r) + P_{r} (r) ⩾ 0, {N E C}_{t} : ρ (r) + P_{t} (r) ⩾ 0, \\ {W E C}_{r} & : & ρ (r) ⩾ 0, ρ (r) + P_{r} (r) ⩾ 0, \\ {W E C}_{t} & : & ρ (r) ⩾ 0, ρ (r) + P_{t} (r) ⩾ 0, \\ S E C & : & ρ (r) + P_{r} (r) + 2 P_{t} (r) ⩾ 0. \end{array} \end{array}

(32)

Figures 5 (left)-6 along with figure 1 (right) make sure that the present solutions satisfy all the energy conditions, and hence, this result is again in favour of representing physical matter distribution inside the fluid configurations.

Figure 6. Characteristic of ρ(r) + P_t(r) (left) and ρ(r) + P_r(r) + 2P_t(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

6. Matching of interior and exterior solutions

In the stellar model, the interior solution will be matched with the exterior Schwarzschild solution at the surface r = R of the star [77]. Indeed, the matching of interior and exterior solutions helps to determine the values of constants involved in the interior solution. The Schwarzschild exterior solution is given as [77]

\begin{array}{rcl} \begin{array}{rcl} {d s}^{2} & = & - (1 - \frac{2 M}{r}) {d t}^{2} + {(1 - \frac{2 M}{r})}^{- 1} {d r}^{2} \\ + r^{2} (d θ^{2} + \sin^{2} θ d ϕ^{2}), \end{array} \end{array}

(33)

where M is the mass of the fluid sphere of radius R.

Now, the matching of interior and exterior solutions at the surface r = R (>2M to avoid the singularity) yields

\begin{array}{rcl} e^{ν (R) / 2} = A + \frac{\sqrt{a} B}{2 b} l o g [\sinh ({b R}^{2} + c)] = {(1 - \frac{2 M}{R})}^{1 / 2}, \end{array}

(34)

\begin{array}{rcl} e^{λ (R)} = 1 + {a R}^{2} \coth^{2} ({b R}^{2} + c) = {(1 - \frac{2 M}{R})}^{- 1}, \end{array}

(35)

Also, the radial pressure P_r(r) at the surface r = R becomes zero i.e. P_r(R) = 0, which yields

\begin{array}{rcl} \begin{array}{l} 4 \sqrt{a} b B - a \coth ({b R}^{2} + c) \\ \times [2 A b + \sqrt{a} B l o g [\sinh ({b R}^{2} + c)]] = 0. \end{array} \end{array}

(36)

Therefore, the boundary conditions (34)–(36) simultaneously provide the following results

\begin{array}{rcl} a = \frac{2 M \tanh^{2} ({b R}^{2} + c)}{R^{2} (R - 2 M)}, \end{array}

(37)

\begin{array}{rcl} \begin{array}{rcl} A & = & \frac{\sqrt{(R - 2 M)}}{4 b \sqrt{R}} [4 b - a \coth ({b R}^{2} \\ + c) l o g [\sinh ({b R}^{2} + c)]], \end{array} \end{array}

(38)

\begin{array}{rcl} B = \frac{\sqrt{a (R - 2 M)} \coth ({b R}^{2} + c)}{2 \sqrt{R}} . \end{array}

(39)

Here, b and c are free parameters to derive well-behaved solutions. Also, the mass M and radius R will be selected accordingly for different stars.

7. Equilibrium analysis

In this section, we will examine the equilibrium of the fluid distributions described by our solutions. For an anisotropic fluid sphere, the gravitational force, hydrostatic force, and anisotropic force together create the equilibrium situation, and this situation can be described by the Tolman–Oppenheimer–Volkoff (TOV) equation. The generalized TOV equation for anisotropic fluid distribution can be written as [86, 87]

\begin{array}{rcl} \begin{array}{rcl} - & \frac{M_{g} (r)}{r^{2}} {ρ (r) + P_{r} (r)} e^{(λ (r) - ν (r)) / 2} \\ - & \frac{{d P}_{r} (r)}{d r} + \frac{2 Δ (r)}{r} = 0, \end{array} \end{array}

(40)

where, M_g(r) stands for the effective gravitational mass. According to the Tolman−Whittaker mass formula M_g(r) can be written as [88]

\begin{array}{rcl} M_{g} (r) = 4 π \int_{0}^{r} (T_{0}^{0} - T_{1}^{1} - T_{2}^{2} - T_{3}^{3}) r^{2} e^{{ν (r) + λ (r)} / 2} d r . \end{array}

(41)

On using the energy-momentum tensor (3) and field equations (4)–(5), equation (41) results

\begin{array}{rcl} M_{g} (r) = \frac{1}{2} r^{2} ν^{'} (r) e^{{ν (r) - λ (r)} / 2} . \end{array}

(42)

Therefore, with the above M_g(r), the TOV equation (40) reads as

\begin{array}{rcl} - \frac{ν^{'} (r) {ρ (r) + P_{r} (r)}}{2} - \frac{{d P}_{r} (r)}{d r} + \frac{2 Δ (r)}{r} = 0, \end{array}

(43)

\begin{array}{rcl} i . e . F_{g} (r) + F_{h} (r) + F_{a} (r) = 0, \end{array}

(44)

where,

F_{g} (r) = - \frac{1}{2} ν^{'} (r) {ρ (r) + P_{r} (r)}

is termed as the gravitational force, F_h(r) = − dP_r(r)/dr is termed as the hydrostatic force, and F_a(r) = 2Δ(r)/r is termed as the anisotropic force.

For the present solutions, the three distinct forces are derived in the following expressions

\begin{array}{rcl} F_{g} (r) = \frac{- [b B ξ_{4} (2 b B r ξ_{4} + ξ_{3} \sqrt{a} \coth ({b r}^{2} + c) + 2 b (B - ξ_{3} \sqrt{a} r^{2} {c s c h}^{2} ({b r}^{2} + c)))]}{[2 π ξ_{3}^{2} {(1 + {a r}^{2} \coth^{2} ({b r}^{2} + c))}^{2}]}, \end{array}

(45)

\begin{array}{rcl} F_{h} (r) = \frac{[2 a r ξ_{1} ξ_{3} (- a ξ_{3} \coth^{2} ({b r}^{2} + c) + B ξ_{5}) - (1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)) ξ_{6}]}{8 π ξ_{3}^{2} {(1 + {a r}^{2} \coth^{2} ({b r}^{2} + c))}^{2}}, \end{array}

(46)

\begin{array}{rcl} F_{a} (r) = \frac{\sqrt{a} r ξ_{2} [\coth ({b r}^{2} + c) {2 \sqrt{a} A b + a B l o g [\sinh ({b r}^{2} + c)]} - 2 b B]}{4 π {[1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)]}^{2} [2 A b + \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]]}, \end{array}

(47)

where

\begin{array}{rcl} \begin{array}{rcl} ξ_{3} & = & 2 A b + \sqrt{a} B l o g (\sinh ({b r}^{2} + c)), \\ ξ_{4} & = & a r \coth^{2} ({b r}^{2} + c), \\ ξ_{5} & = & 4 \sqrt{a} b \coth ({b r}^{2} + c), \\ ξ_{6} & = & ξ_{3}^{2} \sqrt{a} r {c s c h}^{2} ({b r}^{2} + c) - 8 b^{2} B^{2} ξ_{4} \\ - 8 ξ_{3} \sqrt{a} b^{2} B r {c s c h}^{2} ({b r}^{2} + c) . \end{array} \end{array}

(48)

We illustrate the behaviours of these three forces graphically in figure 7 (left), indicating that our solutions depicting fluid configurations are in states of equilibrium.

Figure 7. Characteristics of different forces (left) and radial, transverse velocities of sound (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

8. Stability analysis

The analysis of stability is very crucial in evaluating the viability and consistency of the model of stellar objects. Indeed, the celestial objects that demonstrate stability against external perturbations are particularly intriguing to study. Here, we explore the stability of the model through (i) Causality condition along with stability factor, (ii) Adiabatic index, and (iii) Harrison–Zeldovich–Novikov criterion.

8.1. Causality condition

According to general relativity, nothing can travel faster than light, i.e. the velocity of light is the maximum velocity that ever exists, which is considered to be equal to 1 in the gravitational unit. The causality condition states that the radial velocity v_r(r) and transverse velocity v_t(r) of sound within the physical fluid distribution must be less than the velocity of light, mathematically, 0 ≤ v_r(r), v_t(r) < 1 [89]. Now, v_r(r) and v_t(r) inside the anisotropic compact star are defined as

\begin{array}{rcl} v_{r} (r) = \sqrt{\frac{{d p}_{r} (r)}{d ρ (r)}} a n d v_{t} (r) = \sqrt{\frac{{d p}_{t} (r)}{d ρ (r)}} . \end{array}

(49)

Figure 7 (right) reveals that the present model nicely holds the causality condition, i.e. our model represents physically realistic fluid configurations. Taking into account the concept of cracking of Herrera [90], Abreu et al [91] introduced the stability conditions for the stellar model concerning the stability factor

S_{F} (r) = [{v_{t} (r)}^{2} - {v_{r} (r)}^{2}]

as: the matter configuration is potentially stable if −1 < S_F(r) < 0 and unstable if 0 < S_F(r) < 1. Figure 8 (left) indicates that the present solutions depicted matter configurations are potentially stable.

Figure 8. Characteristics of stability factor (left) and adiabatic index (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

8.2. Adiabatic index

The relativistic adiabatic index serves as a crucial factor in analyzing the stability of stellar fluid spheres by quantifying the change in pressure as the matter density undergoes slight variations. The relativistic adiabatic index Γ_r(r) is defined as [92]

\begin{array}{rcl} Γ_{r} (r) = \frac{ρ (r) + P_{r} (r)}{P_{r} (r)} \frac{{d P}_{r} (r)}{d ρ (r)} . \end{array}

(50)

According to Bondi [92], the stellar Newtonian sphere will be stable if the adiabatic index Γ_r(r) > 4/3 and Γ_r(r) = 4/3 represents the state of neutral equilibrium. Figure 8 (right) shows that the present solutions recommended adiabatic index Γ_r(r) > 4/3, which adds another feather in favour of stable fluid configurations.

8.3. Harrison–Zeldovich–Novikov criterion

According to Harrison–Zeldovich–Novikov [84, 93], the mass should increase with the increase of central density ρ_c for the static stability state of fluid configurations, mathematically, ∂M(ρ_c)/∂ρ_c > 0 for the static stability state. The mass as a function of the central density is obtained as

\begin{array}{rcl} M (ρ_{c}) = \frac{4 π R^{3} ρ_{c} \tanh^{2} (c) \cosh^{2} ({b R}^{2} + c)}{8 π R^{2} ρ_{c} \tanh^{2} (c) \cosh^{2} ({b R}^{2} + c) + 3 \sinh^{2} ({b R}^{2} + c)}, \end{array}

(51)

\begin{array}{rcl} t h e r e f o r e, \frac{\partial M}{\partial ρ_{c}} = \frac{3 π R^{3} \tanh^{2} (c) \sinh^{2} [2 ({b R}^{2} + c)]}{{[8 π R^{2} ρ_{c} \tanh^{2} (c) \cosh^{2} ({b R}^{2} + c) + 3 \sinh^{2} ({b R}^{2} + c)]}^{2}} > 0. \end{array}

(52)

The present solutions satisfy the static stability criterion and thus remain stable, clear from figure 9. Also, we display the mass-surface profile in figure 10 (left), illustrating that the ranges of masses and radii are very close to the observed values.

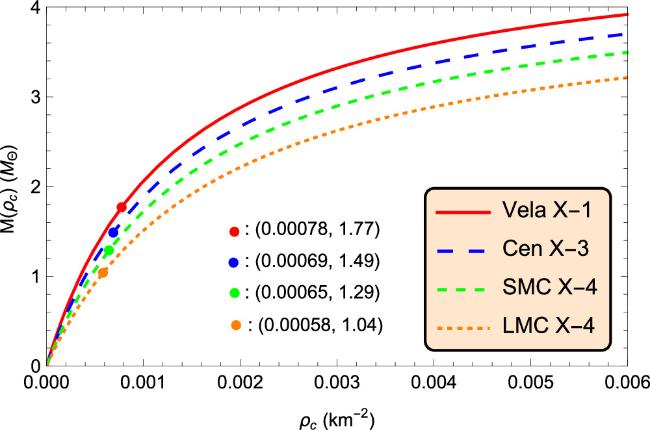
Figure 9. Characteristics of mass against the central density ρ_c corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Full size|PPT slide

Figure 10. Characteristics of mass M against the surface radius R (left) and mass M against the moment of inertia I (right).

Full size|PPT slide

9. Generating functions

In 2008, Herrera [94] devised an algorithm utilizing generating functions to derive all feasible anisotropic solutions of Einstein's field equations as

\begin{array}{rcl} e^{λ (r)} = \frac{K^{2} (r) e^{\int {\frac{4}{r^{2} K (r)} + 2 K (r)} d r}}{r^{6} {C - 2 \int [\frac{K (r) {1 + Π (r) r^{2}}}{r^{8}} e^{\int {\frac{4}{r^{2} K (r)} + 2 K (r)} d r}] d r}}, \end{array}

(53)

where C is the constant of integration and the corresponding generating functions are [94]

\begin{array}{rcl} K (r) = \frac{ν^{'} (r)}{2} + \frac{1}{r}, \end{array}

(54)

\begin{array}{rcl} Π (r) = 8 π [P_{r} (r) - P_{t} (r)] . \end{array}

(55)

Now, employing the class-I condition (12), the generating functions (54)–(55) result

\begin{array}{rcl} K (r) = \frac{B \sqrt{e^{λ (r)} - 1}}{A + B \int \sqrt{e^{λ (r)} - 1} d r} + \frac{1}{r}, \end{array}

(56)

\begin{array}{rcl} Π (r) = 8 π [P_{r} (r) - P_{t} (r)] . \end{array}

(57)

For the present solutions, the generating functions are obtained in the following forms

\begin{array}{rcl} K (r) = \frac{1}{r} + \frac{2 \sqrt{a} b B r \coth ({b r}^{2} + c)}{2 A b \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]}, \end{array}

(58)

\begin{array}{rcl} Π (r) = \frac{\sqrt{a} r^{2} ξ_{2} [2 b B - \coth ({b r}^{2} + c) {2 \sqrt{a} A b + a B l o g [\sinh ({b r}^{2} + c)]}]}{{[1 + {a r}^{2} \coth^{2} ({b r}^{2} + c)]}^{2} [2 A b + \sqrt{a} B l o g [\sinh ({b r}^{2} + c)]]} . \end{array}

(59)

10. Moment of inertia and mass relationship

Bejger and Haensel [95] employed a technique wherein a static solution could transition into a rotating one by utilizing an approximate expression for the moment of inertia I given as

\begin{array}{rcl} I = \frac{2}{5} [1 + \frac{(M / R) \cdot k m}{M_{⊙}}] {M R}^{2} . \end{array}

(60)

The profile of I against mass M is demonstrated in figure 10 (right), which helps to predict the possible approximate moment of inertia against observed ranges of masses.

11. Result and discussions

In this article, we have introduced a new model for static, spherically symmetric anisotropic compact stars in the framework of embedding class-I spacetime. The present solutions are analyzed based on the four well-known compact stars, namely Vela X-1, Cen X-3, SMC X-4, and LMC X-4, and coherently we have found the following key results.

The proposed metric potentials are non-singular inside the compact stars with e^λ(0)=1 and

e^{ν (0)} = {[A + \sqrt{a} B l o g [\sinh (c)] / 2 b]}^{2}

= positive constant, ensuring that the metric potentials are physically fit to generate the physically viable stellar model (see figure 1 (left)).

The energy density and pressures are positively finite throughout the interior of fluid spheres having maximum values at the centers of the fluid spheres, clear from figures 1 (right) and 2 (left). In addition, P_r(R) = 0, P_r(0) = P_t(0), and P_t(r) > P_r(r) for 0 < r ≤ R (see figure 2 (left)), these results ensure that the pressure anisotropic is positive for 0 < r ≤ R and vanishes at the centre (see figure 2 (right)). Indeed, the positive pressure anisotropic creates a repulsive anisotropic force that can assist in constructing a more stable compact star [96]. The symmetric profiles of energy density, radial pressure, and pressure anisotropic have ensured their desired characteristics (see figure 3). The numerical values of central, surface densities and central pressure for the model compact stars are provided in table 2. Interestingly, the central and surface densities both are of order 10¹⁴ gm cm⁻³, and the central pressure is of order 10³⁴ gm cm⁻², these respect the observational data.

The mass m(r) and compactness parameter u(r) are zero at the centres of the stars, after that, monotonically increasing toward the surfaces, clear form figure 4 (left). Buchdahl [80] proposed a clear prediction regarding the maximum attainable mass for relativistic stars as M < 4R/9, or equivalently

2 u (R) < \frac{8}{9}

, this is respected by our solutions (figure 4 (left) and table 2).

The surface redshift Z_s(r) approaches zero at the centres and then steadily increases towards the surfaces of the model spheres. Conversely, the gravitational redshift Z_g(r) exhibits an inverse pattern, reaching its peak at the centres and declining towards the surfaces of the fluid configurations (see figure 4 (right)). Moreover, Z_s(r) and Z_g(r) meet together at the surfaces, i.e. Z(R) = Z_s(R) = Z_g(R). The numerical results for Z(R) given in table 2 respect the range provided by Ivanov [4].

The EoS parameters for the present solutions are nicely fitted in the range 0 < ω_r(r), ω_t(r) < 1 [81] (see figure 5 (left)). Also, the solutions satisfied all the energy conditions, clear from figures 5 (right)–6 along with figures 1 (right). In this context, one can say that our solutions presenting matter configurations are physical.

The model compact stars are in equilibrium positions under the simultaneous action of gravitational, hydrostatic, and anisotropic forces. Indeed, hydrostatic, and anisotropic forces act as repulsive forces to balance the attractive gravitational force, this scenario is clear in figure 7 (left).

The stability of the model is analyzed through the causality condition, adiabatic index, and Harrison–Zeldovich–Novikov criterion. The sound velocities v_r(r) and v_r(r) are positive and less than one (speed of light) (see figure 7 (right)), moreover, the stability factor S_F(r) is negative (see figure 8 (left)), indicating that the solutions represent physically stable matter distributions. Furthermore, the profiles of the adiabatic index (see figure 8 (right)) and mass in terms of central density (see figure 9) also respect the stable scenario of the model fluid configurations. Figure 9 also suggests that the central densities of the model stars are, Vela X-1: 0.000 78 /km², Cen X-3: 0.000 69/km², SMc X-4: 0.000 65/km², and LMC X-4: 0.000 58/km².

The mass-surface radius profile describes the same ranges of masses and radii as given in table 1, i.e. our solutions providing mass and radius ranges are closely matched with the observed values (see figure 10 (left)). In addition, the corresponding moment of inertia I can be deduced from the I − M graph, figure 10 (right) as for Vela X-1: I ≈ 1.483 × 10⁴⁵ g cm²; Cen X-3: I ≈ 1.178 × 10⁴⁵ g cm², SMC X-4: I ≈ 0.897 × 10⁴⁵ g cm², and LMC X-4: I ≈ 0.692 × 10⁴⁵ g cm².

**Table 1. Numerical values of masses, radii, and constants a A, B for four well-known celestial compact stars corresponding to b = 0.0001 /km² and c = 1.**

Compact	M/M_⊙	R (km)	Reference	M/M_⊙	R (km)	a (km⁻²)	A	B
stars	Observed	Observed		Calculated	Calculated
Vela X-1	1.77 ± 0.08	9.560 ± 0.08	[97]	1.77	9.56	0.003 769	−0.900662	0.031 826

Cen X-3	1.49 ± 0.08	9.170 ± 0.13	[97]	1.49	9.17	0.003 351	−0.730014	0.031 083

SMC X-4	1.29 ± 0.05	8.831 ± 0.9	[97]	1.30	8.80	0.003 133	−0.636692	0.030 765

LMC X-4	1.04 ± 0.09	8.301 ± 0.2	[97]	1.04	8.30	0.002 837	−0.503365	0.030 157

It is noted that the physical parameters in this model have followed the same desired behaviours as described in [36–38, 46, 98–107]. Moreover, our obtained numerical results of the physical parameters given in table 2 are very close to the results provided by [39, 48, 108–110] with the values of moment of inertia I in order of 10⁴⁵ g cm² [44, 97, 111]. Therefore, all these behaviours enrich our model for physical acceptability.

Table 2. Numerical values of the central and surface densities, average density ρ_av = 3M/4πR³, central pressure, surface redshift at the boundary, twice of compactness parameter with buchdahl limit, and moment of inertia for four celestial compact stars mentioned in table 1.

Compact	ρ_c × 10¹⁴	ρ_s × 10¹⁴	ρ_av × 10¹⁴	P_c × 10³⁴	z(R)	2u_s	Buchdahl	I(g cm²)
stars	gm cm⁻³	gm cm⁻³	gm cm⁻³	dyne cm⁻²			Limit 80	Aprox.
Vela X-1	10.449 30	4.879 38	6.514 64	5.228 10	0.260 175	0.370 293	$< \frac{8}{9}$	1.483 × 10⁴⁵

Cen X-3	9.290 53	4.842 24	6.213 97	3.672 92	0.217 137	0.324 973	$< \frac{8}{9}$	1.178 × 10⁴⁵

SMC X-4	8.685 69	4.873 49	6.087 41	2.894 82	0.189 450	0.293 182	$< \frac{8}{9}$	0.897 × 10⁴⁵

LMC X-4	7.864 19	4.850 02	5.849 11	2.056 91	0.155 165	0.250 602	$< \frac{8}{9}$	0.692 × 10⁴⁵

Finally, all the significant results ensure that the present model is physically well-behaved and suitable to describe the static, spherically symmetric stable anisotropic compact stars in the framework of embedding class-I spacetime.

References

List( Publishing order | Descend order by publishing year | Descend order by cited within ) Chart analysis

1	Bowers R L, Liang E P T 1974 Anisotropic spheres in general relativity Astrophys. J 188 657 https://doi.org/10.1086/152760 Cited in this article [1]

2	Ruderman R 1972 Pulsars: structure and dynamics Ann. Rev. Astron. Astrophys. 10 427 https://doi.org/10.1146/annurev.aa.10.090172.002235 Cited in this article [1]

3	Herrera L, Santos N O 1997 Local anisotropy in self-gravitating systems Phys. Rep. 286 53 https://doi.org/10.1016/S0370-1573(96)00042-7

4	Ivanov B V 2002 Maximum bounds on the surface redshift of anisotropic stars Phys. Rev. D 65 104011 https://doi.org/10.1103/PhysRevD.65.104011 Cited in this article [2]

5	Schunck F E, Mielke E W 2003 General relativistic boson stars Class. Quantum Gravit. 20 301 https://doi.org/10.1088/0264-9381/20/20/201 Cited in this article [1]

6	Kippenhahn R, Weigert A 1990 Stellar Structure and Evolution Berlin Springer Cited in this article [1]

7	Sokolov A I 1980 Phase transformations in a superfluid neutron liquid JETP 79 1137 Cited in this article [1]

8	Sawyer R F 1972 Condensed phase in neutron-star matter Phys. Rev. Lett. 29 382 https://doi.org/10.1103/PhysRevLett.29.382 Cited in this article [1]

9	Herrera L, Santos N O 1995 Jeans mass for anisotropic matter Astrophys. J. 438 308 https://doi.org/10.1086/175075 Cited in this article [1]

10	Weber F 1999 Pulsars as Astrophysical Observatories for Nuclear and Particle Physics Bristol IOP Publishing Cited in this article [1]

11	Dev K, Gleiser M 2002 Anisotropic stars: exact solutions Gen. Relativ. Gravit. 34 1793 https://doi.org/10.1023/A:1020707906543 Cited in this article [1]

12	Dev K, Gleiser M 2003 Anisotropic stars II: stability Gen. Relativ. Gravit. 35 1435 https://doi.org/10.1023/A:1024534702166 Cited in this article [1]

13	Böhmer C G, Harko T 2006 Bounds on the basic physical parameters for anisotropic compact general relativistic objects Class. Quantum Gravity 23 6479 https://doi.org/10.1088/0264-9381/23/22/023 Cited in this article [1]

14	Chaisi M, Maharaj S D 2005 Compact anisotropic spheres with prescribed energy density General Relativ. Gravit. 37 1177 https://doi.org/10.1007/s10714-005-0102-3 Cited in this article [1]

15	Letelier P S 1980 Anisotropic fluids with two-perfect-fluid components Phys. Rev. D 22 807 https://doi.org/10.1103/PhysRevD.22.807 Cited in this article [1]

16	Bayin S S 1982 Anisotropic fluid spheres in general relativity Phys. Rev. D 26 1262 https://doi.org/10.1103/PhysRevD.26.1262

17	Mak M K, Harko T 2003 Anisotropic stars in general relativity Proc. R. Soc. A 459 393 https://doi.org/10.1098/rspa.2002.1014

18	Herrera L, Di Prisco A, Martin J, Ospino J, Santos N O, Troconis O 2004 Spherically symmetric dissipative anisotropic fluids: a general study Phys. Rev. D 69 084026 https://doi.org/10.1103/PhysRevD.69.084026 Cited in this article [1]

19	Hillebrandt W, Steinmetz K O 1976 Anisotropic neutron star models: stability against radial and nonradial pulsations Astron. Astrophys. 53 283 Cited in this article [1]

20	Doneva D D, Yazadjiev S S 2012 Gravitational wave spectrum of anisotropic neutron stars in Cowling approximation Phys. Rev. D 85 124023 https://doi.org/10.1103/PhysRevD.85.124023

21	Silva H O, Macedo C F B, Berti E, Crispino L C B 2015 Slowly rotating anisotropic neutron stars in general relativity and scalar-tensor theory Class. Quantum Gravity 32 145008 https://doi.org/10.1088/0264-9381/32/14/145008

22	Yagi K, Yunes N 2015 I-Love-Q anisotropically: universal relations for compact stars with scalar pressure anisotropy Phys. Rev. D 91 123008 https://doi.org/10.1103/PhysRevD.91.123008

23	Yagi K, Yunes N 2015 Relating follicly-challenged compact stars to bald black holes: a link between two no-hair properties Phys. Rev. D 91 103003 https://doi.org/10.1103/PhysRevD.91.123008

24	Yagi K, Yunes N 2016 I-Love-Q relations: from compact stars to black holes Class. Quantum Gravity 33 095005 https://doi.org/10.1088/0264-9381/33/9/095005

25	Biswas B, Bose S 2019 Tidal deformability of an anisotropic compact star: implications of GW170817 Phys. Rev. D 99 104002 https://doi.org/10.1103/PhysRevD.99.104002 Cited in this article [1]

26	Heintzmann H, Hillebrandt W 1975 Neutron stars with an anisotropic equation of state-mass, redshift and stability Astron. Astrophys. 38 51 Cited in this article [1]

27	Sharma R 2001 General solution for a class of static charged spheres Gen. Relativ. Gravit. 33 999 https://doi.org/10.1023/A:1010272130226 Cited in this article [1]

28	Alcock C 1986 Strange stars Astrophys. J. 310 261 https://doi.org/10.1086/164679 Cited in this article [1]

29	Haensel P 1986 Strange quark stars Astron. Astrophys. 160 121 Cited in this article [1]

30	Ovalle J 2008 Searching exact solutions for compact stars in braneworld: a conjecture Mod. Phys. Lett. A 23 3247 https://doi.org/10.1142/S0217732308027011 Cited in this article [1]

31	Viznyuk A, Shtanov Y 2007 Spherically symmetric problem on the brane and galactic rotation curves Phys. Rev. D 76 064009 https://doi.org/10.1103/PhysRevD.76.064009 Cited in this article [1]

32	Castroa L B, Alloy M D, Menezes D P 2014 Mass radius relation of compact stars in the braneworld J. Cosmol. Astro. Phys. 08 047 https://doi.org/10.1088/1475-7516/2014/08/047 Cited in this article [1]

33	Karmakar K R 1948 Gravitational metrics of spherical symmetry and class one Proc. Ind. Acad. Sci. A 27 56 https://doi.org/10.1007/BF03173443 Cited in this article [2]

34	Randall L, Sundrum R 1999 Large mass hierarchy from a small extra dimension Phys. Rev. Lett. 83 3370 https://doi.org/10.1103/PhysRevLett.83.3370 Cited in this article [1]

35	Ivanov V 2018 A conformally flat realistic anisotropic model for a compact star Eur. Phys. J. C 78 332 https://doi.org/10.1140/epjc/s10052-018-5825-x Cited in this article [1]

36	Singh K N, Pant N 2016 A family of well-behaved Karmarkar spacetimes describing interior of relativistic stars Eur. Phys. J. C 76 524 https://doi.org/10.1140/epjc/s10052-016-4364-6 Cited in this article [2]

37	Singh K N 2017 A new relativistic stellar model with anisotropic fluid in Karmarkar space-time Annals Phys. 377 256 https://doi.org/10.1016/j.aop.2016.12.029

38	Singh K N 2017 Physical viability of fluid spheres satisfying the Karmarkar condition Eur. Phys. J. C 77 100 https://doi.org/10.1140/epjc/s10052-017-4612-4 Cited in this article [1]

39	Singh K N 2017 A 4D spacetime embedded in a 5D pseudo-euclidean space describing interior of compact stars Eur. Phys. J. A 53 21 https://doi.org/10.1140/epja/i2017-12210-1 Cited in this article [1]

40	Singh K N 2019 A generalized Finch-Skea class one static solution Eur. Phys. J. C 79 381 https://doi.org/10.1140/epjc/s10052-019-6899-9

41	Singh K N 2018 Relativistic fluid spheres with Karmarkar condition Int. J. Mod. Phys. D 27 1950003 https://doi.org/10.1142/S0218271819500032

42	Singh K N, Pant N, Pradhan N 2016 Charged anisotropic Buchdahl solution as an embedding class I spacetime Astrophys. Space Sci. 361 173 https://doi.org/10.1007/s10509-016-2759-3

43	Sarkar N 2019 Anisotropic fluid spheres satisfying the Karmarkar condition Mod. Phys. Lett. A 34 1950113 https://doi.org/10.1142/S021773231950113X

44	Sarkar N 2019 Compact star models in class I spacetime Eur. Phys. J. C 79 516 https://doi.org/10.1140/epjc/s10052-019-7035-6 Cited in this article [1]

45	Bhar P, Maurya S K, Gupta Y K, Manna T 2016 Modelling of anisotropic compact stars of embedding class one Eur. Phys. J. A 52 312 https://doi.org/10.1140/epja/i2016-16312-x

46	Bhar P, Govender M 2017 Anisotropic charged compact star of embedding class I Int. J. Mod. Phys. D 26 1750053 https://doi.org/10.1142/S0218271817500535 Cited in this article [1]

47	Bhar P 2017 A comparative study on generalized model of anisotropic compact star satisfying the Karmarkar condition Eur. Phys. J. C 77 596 https://doi.org/10.1140/epjc/s10052-017-5149-2

48	Bhar P 2017 A new class of relativistic model of compact stars of embedding class I Int. J. Mod. Phys. D 26 1750090 https://doi.org/10.1142/S0218271817500535 Cited in this article [1]

49	Bhar P 2017 A charged anisotropic well-behaved Adler-Finch-Skea solution satisfying Karmarkar condition Int. J. Mod. Phys. D 26 1750078 https://doi.org/10.1142/S0218271817500535

50	Thakadiyil S, Jasim M K 2013 Invariant solutions of Einstein's field equations for conformally flat fluid spheres of embedding class one Int. J. Theor. Phys. 52 3960 https://doi.org/10.1007/s10773-013-1708-y

51	Maurya S K, Govender M 2017 Generating physically realizable stellar structures via embedding Eur. Phys. J. C 77 347 https://doi.org/10.1140/epjc/s10052-017-4916-4

52	Maurya S K, Gupta Y K, Smitha T T, Rahaman F 2016 A new exact anisotropic solution of embedding class one Eur. Phys. J. A 52 191 https://doi.org/10.1140/epja/i2016-16191-1

53	Maurya S K, Ratanpal B S, Govender M 2017 Anisotropic stars for spherically symmetric spacetimes satisfying the Karmarkar condition Ann. Phys. 382 36 https://doi.org/10.1016/j.aop.2017.04.008

54	Maurya S K, Govender M 2017 A family of charged compact objects with anisotropic pressure Eur. Phys. J. C 77 420 https://doi.org/10.1140/epjc/s10052-017-4982-7

55	Maurya S K, Banerjee A, Hansraj S 2018 Role of pressure anisotropy on relativistic compact stars Phys. Rev. D 97 044022 https://doi.org/10.1103/PhysRevD.97.044022

56	Kasner E 1921 Finite representation of the solar gravitational field in flat space of six dimensions Am. J. Math. 43 130 https://doi.org/10.2307/2370246 Cited in this article [2]

57	Gupta Y K, Goel M P 1975 Class two analogue of TY Thomas's theorem and different types of embeddings of static spherically symmetric space-times Gen. Rel. Grav. 6 499 https://doi.org/10.1007/BF00762454 Cited in this article [1]

58	Eddington Kasner A S 1924 The Mathematical Theory of Relativity Cambridge Cambridge University Press Cited in this article [1]

59	Friedmann A 1922 The curve of the raumes Zeit. Physik. 10 377 https://doi.org/10.4159/harvard.9780674366688.c134 Cited in this article [1]

60	Robertson H P 1933 Relativistic cosmology Rev. Mod. Phys. 5 62 https://doi.org/10.1103/RevModPhys.5.62

61	Lemaître G 1927 Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques Ann. Soc. Sci. Bruxelles, Ser. 47 49 Cited in this article [1]

62	Kuzeev R R 1980 Inmersion class of a Kerr field Gravit. Teor. Otnosit. 16 93 Cited in this article [1]

63	Chodil G 1967 X-ray intensities and spectra from several cosmic sources Astrophys. J. 150 57 https://doi.org/10.1086/149312 Cited in this article [2]

64	Giacconi R 1972 The Uhuru catalog of X-ray sources Astrophys. J. 178 281 https://doi.org/10.1086/151790 Cited in this article [2]

65	Hanke M 2007 Studying the stellar wind in the Vela X-1 system Cited in this article [1]

66	Giacconi R, Gursky H, Kellog E, Schreier E, Tananbaum H 1971 Discovery of periodic X-ray pulsations in Centaurus X-3 from UHURU Astrophys. J. 167 67 https://doi.org/10.1086/180762 Cited in this article [1]

67	Schreie E, Levinson R, Gursky H, Kellog E, Tananbaum H, Giacconi R 1972 Evidence for the Binary Nature of Centaurus X-3 from UHURU X-Ray Observations Astrophys. J. 172 79 https://doi.org/10.1086/180896 Cited in this article [1]

68	Price R E 1971 X-rays from the Magellanic Clouds Astrophys. J. 168 L7 https://doi.org/10.1086/180773 Cited in this article [1]

69	Leong C, Kellogg E, Gursky H, Tananbaum H, Giacconi R 1971 X-ray emission from the magellanic clouds observed by UHURU Astrophys. J. 170 L67 https://doi.org/10.1086/180842 Cited in this article [1]

70	Schreier E, Giacconi R, Gursky H, Kellogg E, Tananbaum H 1972 Discovery of the binary nature of SMC X-1 from UHURU Astrophys. J. 178 L71 https://doi.org/10.1086/181086 Cited in this article [1]

71	Chevalier C, Ilovaisky S A 1977 The binary nature of the LMC X-4 optical candida Astron. Astrophys. 59 L9 Cited in this article [1]

72	Stephani H, Kramer D, Maccallum M, Hoenselaers C, Helrt E 2003 Exact Solutions of Einstein Field Equations Monographs on Mathematical Physics 2nd edn Cambridge Cambridge University Press Cited in this article [1]

73	Bondi H 1964 Massive spheres in general relativity Proc. Roy. Soc. Lond. A 282 303 317 https://doi.org/10.1098/rspa.1964.0234 Cited in this article [1]

74	Herrera L 1985 Isotropic and anisotropic charged spheres admitting a one-parameter group of conformal motions J. Math. Phys. 26 2302 https://doi.org/10.1063/1.526813 Cited in this article [1]

75	Pandey S N, Sharma S P 1981 Insufficiency of Karmarkar's condition Gen. Relativ. Gravit. 14 113 https://doi.org/10.1007/BF00756917 Cited in this article [2]

76	Maurya S K, Gupta Y K, Ray S, Chowdhury S R Spherically symmetric electromagnetic mass models of embedding class one arXiv:1506.02498 Cited in this article [1]

77	Schwarzschild K 1916 Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie Sitz. Deut. Akad. Winn. Math-Phys. Berlin 24 424 Cited in this article [3]

78	Kohler M, Chao K L 1965 Zentralsymmetrische statische Schwerefelder mit Räumen der Klasse 1 Z. Naturforsch. Ser. A 20 1537 https://doi.org/10.1515/zna-1965-1201 Cited in this article [1]

79	Mak M K, Harko T 2003 Anisotropic stars in general relativity Proc. R. Soc. Lond. A 459 393 https://doi.org/10.1098/rspa.2002.1014 Cited in this article [2]

80	Buchdahl H A 1959 General relativistic fluid spheres Phys. Rev. 116 1027 https://doi.org/10.1103/PhysRev.116.1027 Cited in this article [3]

81	Rahaman F, Ray S, Jafry A K, Chakraborty K 2010 Singularity-free solutions for anisotropic charged fluids with Chaplygin equation of state Phys. Rev. D 82 104055 https://doi.org/10.1103/PhysRevD.82.104055 Cited in this article [3]

82	Hawking S W, Ellis G F R 1973 The Large Scale Structure of Space-Time Cambridge Cambridge University Press Cited in this article [2]

83	Wald R M 1984 General Relativity Chicago, IL University of Chicago Press Cited in this article [2]

84	Zeldovich Y, Novikov I D 1971 Relativistic Astrophysics Vol. 1: Stars and Relativity Chicago, IL University of Chicago Press Cited in this article [2]

85	Negele J W, Vautherin D 1973 Neutron star matter at sub-nuclear densities Nucl. Phys. A 207 298 https://doi.org/10.1016/0375-9474(73)90349-7 Cited in this article [1]

86	Oppenheimer J R, Volkoff G M 1939 On massive neutron cores Phys. Rev. 55 374 https://doi.org/10.1103/PhysRev.55.374 Cited in this article [2]

87	Tolman R C 1939 Static solutions of Einstein's field equations for spheres of fluid Phys. Rev. 55 364 https://doi.org/10.1103/PhysRev.55.364 Cited in this article [1]

88	Devitt J, Florides P S 1989 A modified Tolman mass-energy formula Gen. Relativ. Gravit. 21 585 https://doi.org/10.1007/BF00760620 Cited in this article [1]

89	Abreu H, Hernandez H, Nunez L A 2007 Sound speeds, cracking and the stability of self-gravitating anisotropic compact objects Class. Quantum Gravity 24 4631 https://doi.org/10.1088/0264-9381/24/18/005 Cited in this article [1]

90	Rawls M L, Orosz J A, McClintock J E, Torres M A P, Bailyn C D, Buxton M M 2011 Refined neutron star mass determinations for six eclipsing x-ray pulsar binaries Astrophys. J. 730 25 https://doi.org/10.1088/0004-637X/730/1/25 Cited in this article [1]

91	Herrera L 1992 Cracking of self-gravitating compact objects Phys. Lett. A 165 206 https://doi.org/10.1016/0375-9601(92)90036-L Cited in this article [1]

92	Bondi H 1964 The contraction of gravitating spheres Proc. R. Soc. London A 281 39 https://doi.org/10.1098/rspa.1964.0167 Cited in this article [2]

93	Harrison B K, Thorne K S, Wakano M, Wheeler J A 1965 Gravitational Theory and Gravitational Collapse Chicago, IL University of Chicago Press Cited in this article [1]

94	Herrera L, Ospino J, Parisco A D 2008 All static spherically symmetric anisotropic solutions of Einstein's equations Phys. Rev. D 77 027502 https://doi.org/10.1103/PhysRevD.77.027502 Cited in this article [2]

95	Bejger M, Haensel P 2002 Moments of inertia for neutron and strange stars: limits derived for the Crab pulsar A& A 396 917 https://doi.org/10.1051/0004-6361:20021241 Cited in this article [1]

96	Gokhroo M K, Mehra A L 1994 Anisotropic spheres with variable energy density in general relativity Gen. Relativ. Gravit. 26 75 https://doi.org/10.1007/BF02088210 Cited in this article [1]

97	Chen R, Herrera L, Santos N O 1993 Dynamical instability for radiating anisotropic collapse Mon. Not. R. Astron. Soc. 265 533 https://doi.org/10.1093/mnras/265.3.533 Cited in this article [5]

98	Tello-Ortiz F 2019 Anisotropic relativistic fluid spheres: an embedding class I approach Eur. Phys. J. C 79 885 https://doi.org/10.1140/epjc/s10052-019-7366-3 Cited in this article [1]

99	Bhar P 2019 Anisotropic compact star model: a brief study via embedding Eur. Phys. J. C 79 1 13 https://doi.org/10.1140/epjc/s10052-019-6642-6

100	Bhar P 2017 Modelling a new class of anisotropic compact stars satisfying the Karmarkar's condition Eur. Phys. J. Plus 132 1 12 https://doi.org/10.1140/epjp/i2017-11586-5

101	Singh K, Bhar P, Pant N 2016 A new solution of embedding class I representing anisotropic fluid sphere in general relativity Int. J. Mod. Phys. D 25 1650099 https://doi.org/10.1142/S0218271816500991

102	Fuloria P 2018 A new generalised solution to generate anisotropic compact star models in the Karmarkar space-time manifold Eur. Phys. J. A 54 1 11 https://doi.org/10.1140/epja/i2018-12615-2

103	Jasim M K, Maurya S K, Al-Sawaii A S M 2020 A generalised embedding class one static solution describing anisotropic fluid sphere Astrophys. Space Sci. 365 9 https://doi.org/10.1007/s10509-020-3724-8

104	Satyanarayana G, Bisht R K, Pant N 2020 Relativistic modelling of stellar objects using embedded class one spacetime continuum Mod. Phys. Lett. A 35 2050097 https://doi.org/10.1142/S0217732320500972

105	Baskey L, Das S, Rahaman F 2021 An analytical anisotropic compact stellar model of embedding class I Mod. Phys. Lett. A 36 2150028 https://doi.org/10.1142/S0217732321500280

106	Tayyaba N, Usman A, Shamir M F 2021 Embedded class-I solution of compact stars in f(R) gravity with Karmarkar condition Ann. Phys. 429 168491 https://doi.org/10.1016/j.aop.2021.168491

107	Pandya D M 2020 Anisotropic compact star model satisfying Karmarkar conditions Astrophys. Space Sci. 365 30 https://doi.org/10.1007/s10509-020-3742-6 Cited in this article [1]

108	Maurya S K, Ratanpal B S, Govender M 2017 Anisotropic stars for spherically symmetric spacetimes satisfying the Karmarkar condition Ann. Phys. 382 36 49 https://doi.org/10.1016/j.aop.2017.04.008 Cited in this article [1]

109	Maurya S K, Maharaj S D 2017 Anisotropic fluid spheres of embedding class one using Karmarkar condition Eur. Phys. J. C 77 328 https://doi.org/10.1140/epjc/s10052-017-4905-7

110	Singh K 2017 Conformally non-flat spacetime representing dense compact objects Mod. Phys. Lett. A 32 1750093 https://doi.org/10.1142/S0217732317500936 Cited in this article [1]

111	Bhar P 2017 Modelling a new class of anisotropic compact stars satisfying the Karmarkar's condition Eur. Phys. J. Plus 132 274 https://doi.org/10.1140/epjp/i2017-11586-5 Cited in this article [1]

Acknowledgments

FR would like to thank the authorities of the Inter-University Centre for Astronomy and Astrophysics, Pune, India for providing research facilities. We are thankful to the reviewers for their constructive suggestions.

RIGHTS & PERMISSIONS

PDF(1128 KB)

Accesses

Citation

Detail

Sections

Recommended

Abstract
Key words
Cite this article
1. Introduction
2. Einstein's field equations
3. The Karmarkar condition
4. New solutions via the Karmarkar condition
5. Physical characteristics
5.1. Evaluation of physical parameters
Figure 1. Characteristics of metric potentials (left) and energy density (right) against the radial coordinate r corresponding to the numerical values of constants given in table 1 for four well-known compact stars.
Figure 2. Characteristics of radial and transverse pressures (left) and anisotropic factor (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.
Figure 3. Symmetric profiles of energy density (red centres), radial pressure (yellow centres), and anisotropic factor (green centres) corresponding to numerical values of constants given in table 1 for four well-known compact stars.
Figure 4. Characteristic of mass, compactness parameters (left) and surface, gravitational redshifts (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.
5.2. Equation of state parameters
Figure 5. Characteristic of EoS parameters (left) and ρ(r) + Pr(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.
5.3. Energy conditions
Figure 6. Characteristic of ρ(r) + Pt(r) (left) and ρ(r) + Pr(r) + 2Pt(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.
6. Matching of interior and exterior solutions
7. Equilibrium analysis
Figure 7. Characteristics of different forces (left) and radial, transverse velocities of sound (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.
8. Stability analysis
8.1. Causality condition
Figure 8. Characteristics of stability factor (left) and adiabatic index (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.
8.2. Adiabatic index
8.3. Harrison–Zeldovich–Novikov criterion
Figure 9. Characteristics of mass against the central density ρc corresponding to numerical values of constants given in table 1 for four well-known compact stars.
Figure 10. Characteristics of mass M against the surface radius R (left) and mass M against the moment of inertia I (right).
9. Generating functions
10. Moment of inertia and mass relationship
11. Result and discussions
Table 1. Numerical values of masses, radii, and constants a A, B for four well-known celestial compact stars corresponding to b = 0.0001 /km2 and c = 1.
Table 2. Numerical values of the central and surface densities, average density ρav = 3M/4πR3, central pressure, surface redshift at the boundary, twice of compactness parameter with buchdahl limit, and moment of inertia for four celestial compact stars mentioned in table 1.
References
Acknowledgments
RIGHTS & PERMISSIONS

Received	Accepted	Published
2024-05-26	2024-09-09	2025-01-01
Issue Date
2024-11-08

模态框（Modal）标题

Please choose a citation manager

Content to export

Abstract

Key words

Cite this article

1. Introduction

2. Einstein's field equations

3. The Karmarkar condition

4. New solutions via the Karmarkar condition

5. Physical characteristics

5.1. Evaluation of physical parameters

Figure 1. Characteristics of metric potentials (left) and energy density (right) against the radial coordinate r corresponding to the numerical values of constants given in table 1 for four well-known compact stars.

Figure 2. Characteristics of radial and transverse pressures (left) and anisotropic factor (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Figure 3. Symmetric profiles of energy density (red centres), radial pressure (yellow centres), and anisotropic factor (green centres) corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Figure 4. Characteristic of mass, compactness parameters (left) and surface, gravitational redshifts (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

5.2. Equation of state parameters

Figure 5. Characteristic of EoS parameters (left) and ρ(r) + Pr(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

5.3. Energy conditions

Figure 6. Characteristic of ρ(r) + Pt(r) (left) and ρ(r) + Pr(r) + 2Pt(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

6. Matching of interior and exterior solutions

7. Equilibrium analysis

Figure 7. Characteristics of different forces (left) and radial, transverse velocities of sound (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

8. Stability analysis

8.1. Causality condition

Figure 8. Characteristics of stability factor (left) and adiabatic index (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

8.2. Adiabatic index

8.3. Harrison–Zeldovich–Novikov criterion

Figure 9. Characteristics of mass against the central density ρc corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Figure 10. Characteristics of mass M against the surface radius R (left) and mass M against the moment of inertia I (right).

9. Generating functions

10. Moment of inertia and mass relationship

11. Result and discussions

Table 1. Numerical values of masses, radii, and constants a A, B for four well-known celestial compact stars corresponding to b = 0.0001 /km2 and c = 1.

Table 2. Numerical values of the central and surface densities, average density ρav = 3M/4πR3, central pressure, surface redshift at the boundary, twice of compactness parameter with buchdahl limit, and moment of inertia for four celestial compact stars mentioned in table 1.

{{custom_sec.title}}

{{custom_sec.title}}

References

{{custom_fnGroup.title_en}}

Footnotes

Acknowledgments

{{custom_ack.title_en}}

RIGHTS & PERMISSIONS

Figure 5. Characteristic of EoS parameters (left) and ρ(r) + P_r(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Figure 6. Characteristic of ρ(r) + P_t(r) (left) and ρ(r) + P_r(r) + 2P_t(r) (right) against the radial coordinate r corresponding to numerical values of constants given in table 1 for four well-known compact stars.

Figure 9. Characteristics of mass against the central density ρ_c corresponding to numerical values of constants given in table 1 for four well-known compact stars.

**Table 1. Numerical values of masses, radii, and constants a A, B for four well-known celestial compact stars corresponding to b = 0.0001 /km² and c = 1.**

Table 2. Numerical values of the central and surface densities, average density ρ_av = 3M/4πR³, central pressure, surface redshift at the boundary, twice of compactness parameter with buchdahl limit, and moment of inertia for four celestial compact stars mentioned in table 1.