1. Introduction
Colloidal crystals present an interesting model of condensed matter systems where atoms and electrons are substituted by charged colloidal macroions and small, mobile electrolyte ions [
1]. They can form in systems with purely repulsive long-range interactions [
2–
5] or in systems with combined short-range attraction and long-range repulsion [
6]. The Deryaguin–Landau–Verwey–Overbeek (DLVO)-type interactions between these constituents can be modified and engineered [
7], yielding valuable insights not only into the properties of colloidal crystals themselves but also illuminating the theoretical foundations of atomic and molecular materials such as crystalline elasticity, crystal melting and lattice defects and dynamics, to name just a few [
1,
8,
9]. Colloids of various components and different size/charge asymmetries have been assembled into diverse crystalline structures and have served as experimental models to study phase behaviors and self-assembly processes [
1,
10]. Of particular interest are the binary colloidal crystals where the smaller, mobile component occupies interstitial space in the lattice, formed by the larger colloid component, and can exhibit a localized-to-delocalized transition [
11,
12], as is the case in size-asymmetric DNA-functionalized nanoparticles [
1]. A similar type of behavior is also known to occur in a two-dimensional (2D) crystalline array of cylindrical macroions with interstitial linear polyelectrolyte chains exhibiting a behavior analogous to that of electrons in a 2D crystal [
13]. In the context of colloidal crystals, this localized-to-delocalized transition has been dubbed the ionic to metallic transition [
12].
Attractive interactions between like-charged colloidal particles that cannot be rationalized within the DLVO paradigm [
14], first seen in detailed electrostatic double-layer simulations [
15], have been directly observed in various experiments [
16,
17] and have been studied extensively in the framework of different theoretical approaches [
18] without, however, any clearcut consensus emerging as to their underlying universal mechanism(s). This embarras de richesses [
19] in theoretical understanding of the non-DLVO colloid interactions stems partially from different microscopic models and partially from different approximations applied to solve these models. Among the variations on the model theme we can refer to the most recent proposal of charge regulation at the interacting colloid surfaces yielding an accurate description of the observed force profiles, including their attractive part, down to a few nm [
16,
20,
21]. On the other hand, the departure from the mean-field approximation is still best rationalized in terms of the weak–strong coupling dichotomy of confined Coulomb fluids that yields an attractive electrostatic interaction between identical colloids [
15,
18].
As a consequence, discovering new phenomena that display some novel features of the remaining unexamined life of the anomalous attractive forces in charged colloids are thus certainly worth focusing on in more detail [
17]. Elastic deformation effects are ubiquitous in crystalline solids [
22] where various defects, such as dislocations, interstitials and vacancies, create elastic displacement fields that allow them to interact with long-range interactions [
8,
9,
23–
25]. These lattice Hookian elasticity-mediated forces between point-defects have been shown to be attractive, leading in the case of interstitials and vacancies to the formation of defect strings despite the purely repulsive forces between the colloidal particles [
8,
9,
26,
27]. While the phenomenology of these lattice-mediated attractions bears some similarity to the anomalous attractions between identically charged colloids (see above), the underlying mechanism seems to be quite different and involves an additional (elastic) degree of freedom. Similar lattice-mediated attractions can be surmised to exist between diffusing test charges in the interstitial mobile Coulomb fluid but modified by the ubiquitous electrostatic interactions. This situation is superficially reminiscent of the phonon-mediated attractions between electrons in superconductor Cooper pairing [
28] but, of course, lacks its quantum basis, and therefore could be called ‘thermal Cooper pairing' [
29]. Motivated by these findings, we will attempt to formulate the simplest possible continuum model of the electrostatic-elastic coupling in a model colloidal crystal and ascertain to what extent it mimicks the behavior of other solid state systems.
In what follows we will present a mean-field continuum model of a background 3D crystalline lattice with an interstitial Coulomb fluid and calculate explicitly the effective interaction between two test interstitial charges. The model is based on continuum elasticity of the crystalline lattice and Poisson–Boltzmann (PB) mean-field electrostatics for the interstitial small, mobile ion component. In addition, we will assume a minimal electrostatic-elastic coupling due to the colloidal lattice–mobile ion interactions, which implies a local lattice dilation/constriction at the location of an interstitial mobile charge. In thermodynamic equilibrium this coupling will lead to two equilibrium equations: a modified Navier equation for the elastic displacement and a modified PB equation for the electrostatic field. Linearizing and solving these two equations explicitly for a test point interstitial charge, we derive an effective interaction between two interstitial test sources that displays a variable attractive component depending on the strength of the bare electrostatic screening as well as the electrostatic-elastic coupling. Notably and contrary to the anomalous attraction in other colloidal systems (see above), the effective attraction emerges already on the mean-field level, the reason being that the electrostatic-elastic coupling leads to a two-field theory and thus straightforwardly implies a decrease of the total interaction free energy.
2. Minimal coupling model: mean-field theory
We consider a minimal model describing the electrostatic-elastic coupling as follows: we have an ideal colloid crystalline lattice of charged macroions, see figure
1, embedded in a bathing Coulomb fluid of mobile univalent positive and negative ions, in thermal equilibrium with a bulk phase. In the spirit of a continuum theory, both of the components, the mobile ions as well as the lattice colloids, are assumed to be point-like. In addition, we assume that the lattice colloids can exhibit only small deviations from their equilibrium lattice positions, while the bathing Coulomb fluid ions are fully mobile.
Figure 1. A colloidal lattice contains an interstitial charged ‘intrusion'. A negative (red circle) or positive (blue circle) interstitial test charge imposes a local elastic dilation (orange arrow) or contraction (brown arrow) on the ideal negatively charged colloidal crystal lattice (magenta circle). The interstitial charge therefore induces a local change in volume/density of the lattice. |
Full size|PPT slide
Within this model we assume the free energy of the system as being decomposable into an elastic part, describing the lattice colloids, and an electrostatic part, describing the mobile Coulomb fluid, as well as a minimal coupling part that connects the electrostatic field with elastic deformation. Our aim is then to calculate an effective electrostatic-elastic interaction between two point-like interstitial test particles (‘intrusions') immersed in the system that interact with the Coulomb fluid components electrostatically as well as with the background colloidal lattice elastically.
The electrostatic free energy of the Coulomb fluid is furthermore assumed to coincide with the standard PB free energy [
14], while the elastic energy of the colloidal lattice is of a standard Hookeian form, allowing a further simplification if one assumes that the elastic medium is isotropic [
22]. The elastic constants can be expressed as lattice sums of the interaction potential between colloid macroions in an undistorted lattice [
9], which is furthermore assumed to be three-dimensional [
30]. Finally, the electrostatic-elastic coupling term embodies the effect that the interstitial charges have on the dilation (or contraction) of the background colloidal lattice. It features in two different contexts: the first is the coupling between the Coulomb fluid charge density and the elastic displacement, and the second one is the coupling between the test charge particles and the neighboring background colloidal lattice. The two characteristics have both been included in our recent letter [
29].
The electrostatic free energy is based on the mean-field PB description and is composed of an electrostatic energy and an ideal gas entropy of the mobile ions. It can be written in different equivalent forms, either in the form of a density functional theory [
31] or a field theory [
32]. We choose here a hybrid description of the form [
14]
where
ϵ is proportional to the dielectric permittivity,
e0 is the elementary charge,
n± are the densities of the diffusing mobile ions,
μ± =
μ0 are their chemical potentials, which are identical since the mobile components are electroneutral in the bulk,
φ is the mean electrostatic potential, while
ρe here and below corresponds to the source term pertaining to the point-like test charge source at the origin, with the density
ρe =
δ(
x). Just as in the case of the (linearized) PB theory, the test charge will allow us to calculate the electrostatic potential and the charge–charge interaction. The minimization of this free energy yields the PB equation and the chemical potentials are expressed by the concentrations of the ions in the bulk.
For the elastic part, we first of all rewrite the standard Hookeian elastic free energy for an isotropic elastic medium that is usually written in the form [
22]
where
ui is the elastic displacement vector,
fi is the external force density,
uik is the symmetrized deformation tensor, while
λ and
μ are Lamé coefficients, which can be expressed as lattice sums of the undistorted lattice [
9]. The last term is the source term, pertaining to the point-like interstitial elastic test source at the origin. The source term in equation (
1) and the source term in equation (
2) both correspond to a test particle at the origin, but the former describes its electrostatic interaction and the latter describes its elastic interaction with the system.
The elastic constants can be obtained straightforwardly in the absence of thermal effects, starting from the total energy of the colloidal crystal [
9]
where (∣
ri −
rj∣) is the pair potential between colloid particles
i and
j in the undistorted lattice. Its form is often assumed to coincide with the Debye–Hückel (DH) interaction with an effective charge of the colloid [
2–
5] that includes the effects of distorted double layers at high macroion volume fractions, but it should also include the details of the dissociation process, which are more difficult to incorporate. From here, in the case of an isotropic elastic material, one can derive the following identities for the Lamé elastic constants
λ and
μ [
33,
34]
where
and ″(
r) are the first and second derivative of the pair potential, respectively,
ρ is the colloid number density and
ri is the distance of particle
i from the origin. In the summation the floating prime indicates that we pick one colloid at the center and sum over all the neighbors. The colloid–colloid interaction potential is—at least in part—connected with electrostatic interactions [
35] and thus follows from the electrostatic free energy with colloidal charges as external sources [
36].
We now cast the Hookeian elastic energy into a different form by inserting the symmetrized deformation tensor
into equation (
2), while using the Gauss theorem for the terms that can be cast into the form of a divergence. We thus obtain the elastic free energy as a sum of a volume integral and a surface integral, where the former contains only the scalar invariants composed of
∇ ·
u and
∇ ×
u, plus some irrelevant surface terms
6. This is of course possible only in the case of an isotropic elastic medium. Since the colloid crystal is an anisotropic elastic medium, this is an approximation that ignores the directional aspects of the elastically mediated interaction but, on the other hand, allows for a simplified derivation of the salient features of the positional dependence.
In addition, the source term of equation (
2), corresponding to a point-like interstitial test particle in the elastic medium, can be modified by taking into account that the point-like body force can be written as
f =
v0(
λ + 2
μ)
∇ρe [
9,
37], where
v0 is the local volume change induced by the point-like test particle, acting as a local dilation/contraction center, see figure
1. In fact,
v0 of a point-like interstitial test particle plays the same role in elastic interactions as
e0 of a point-like charge plays in the electrostatic interactions, and the relaxation of the deformation away from the test particle is described by the Navier equation and the electrostatic potential by the PB equation.
Furthermore, it is clear that for an infinite sample volume one can derive the equality
which allows us to write the elastic source term in an analogous form as in the electrostatic free energy equation (
1). Effectively the same form of the elastic coupling, based on a 2D point interstitial defect modelled by two orthogonal pairs of forces, has been used in [
9]. The couplings of the elastic displacement field and the electrostatic potential to the density of the interstitial test particles
ρe are thus completely analogous and given by
for the elastic and the electrostatic case, respectively. Clearly,
v0(
λ + 2
μ) plays the role of an effective elastic ‘charge'.
With these provisos the elastic energy of an isotropic elastic medium then assumes a much simplified final form
Note the analogy but also the fundamental difference between the electrostatic and the elastic free energies: while the former one is formulated in terms of the scalar field and, after an expansion to the second order, exhibits (Debye) screening, the latter is formulated in terms of a vector field and does not exhibit any screening, remaining ‘critical' (i.e. having an inifinite screening length) for all values of the parameters. This is a general property of the elastic Hamiltonians in soft condensed matter that further implies Casimir-like phenomena in e.g. nematic, smectic and cholesteric liquid crystals [
38,
39].
To the electrostatic and elastic free energies we now add an explicit minimal coupling term, corresponding to an energy cost associated with dilatation/contraction of the colloidal lattice due to a local excess of positive or negative mobile charge. Since in an ideal crystal there is a one-to-one mapping of particles to lattice positions [
40], the relation between the density change,
δc, of the colloidal lattice with mean density
c, and the divergence of the displacement field can be written as [
41]
In our model, we assume that the local density change of the colloidal lattice is a consequence of the local mobile charge density mismatch proportional to (
n+ −
n−), and therefore the electrostatic-elastic minimal coupling term can be assumed to have the form
consistent with equation (
6) and based upon the assumption that the density change for positive and negative ions is the same but of opposite sign. We additionally assumed that the elastic coupling is the same—except for the sign—for both types of mobile charges, so there is only a single coupling constant. The above coupling term is just the first term in a series of higher-order symmetry-permitted scalar invariants that we will not consider explicitly in this work.
Gathering all the contributions to the free energy in this minimal model of electrostatic-elastic coupling, the total free energy is then given by
and the thermodynamic equilibrium is described by the corresponding Euler–Lagrange (EL) variational equations that are of the form
as well as
The explicit form of these equations is as follows. For the mobile charges
For the electrostatic potential we derive a modified Poisson equation, and for the elastic displacement we derive a modified Navier equation
These equations can be cast into a much simpler form by introducing the charge density of the mobile ions
Note the difference:
ρ is the mean-field charge density, while
ρe is the external test particle source density.
The first equation in equation (14) presents a generalization of the PB equation, while the second one generalizes the Navier equation. Without the source term, the mean-field solution corresponds to the bulk state of vanishing electrostatic potential and vanishing elastic displacement.
We now invoke the standard Helmholtz decomposition [
9] for the elastic displacement field in terms of the scalar (Φ) and vector (
A) elastic potentials
representing the curl-free longitudinal and the divergence-free transversal part of the elastic deformation. Since all the electrostatic-elastic couplings in the free energy equation (
10) are in terms of
∇ ·
u, we can assume the trivial solution
[
9] for an infinite sample. In addition, in the spirit of the DH approximation [
14], we linearize the charge density to obtain
with
, where
n0 is the density in the bulk reservoir. Just as in the case of the standard DH theory of Coulomb fluids, the linearization ansatz is consistent if
Since for point-like test particles both the electrostatic and the elastic potentials formally diverge at the source, see next section for details, one would need to introduce a finite-size core inside which the theory breaks down, which actually means one should use effective values for both
e0 and
v0.
This linearization furthermore implies that the electrostatic free energy equation (1) is expanded to the second order in the charge density and/or potential, effectively leading to Debye screening of electrostatics. Since, as we already noted, the elastic energy equation (7) is ‘critical' and implies no separate elastic screening, one can expect that the coupled description will also yield only one type of electrostatic screening.
Taking into account the linearization and the Helmholtz decomposition of the elastic displacement, we end up with the following coupled set of linear equations
where the electrostatic-elastic coupling terms are characterized by the product
e0v0. The solution of these two equations gives the electrostatic potential and the elastic potential in the system up to the lowest order electrostatic-elastic coupling terms.
3. Electrostatic and elastic deformation fields
The EL equations, equation (19), can now be solved explicitly for a point-like test particle with an electrostatic charge e0, and an elastic ‘charge' v0(λ + 2μ), described by a delta function-like density ρe = δ(r) located at the origin. The solution yields the spatial relaxation of the mobile ion charge density, ∇ · E = − ϵ∇2φ, and the colloid lattice relative density change , δc/c = ∇ · u, away from the origin.
The solution of this set of linear equations can be obtained straightforwardly and we omit the unnecessary details. The electrostatic potential, proportional to the electrostatic charge of the test particle
e0, has the form
with
with
the electrostatic-elastic coupling constant and
the inverse square of the standard Debye screening length. Since
ξ ≥ 0 it follows that the screening length with electrostatic-elastic coupling decreases compared to the standard Debye screening length. The electrostatic field is then obtained from
and describes the spatial relaxation of the mobile ion charge density proportional to
∇ ·
E. The elastic deformation potential, proportional to the elastic ‘charge'
v0(
λ + 2
μ), has the form
and taking into account
u =
∇Φ, we have the elastic deformation vector in the medium as
describing the spatial relaxation of the colloid lattice relative density change,
∇ ·
u, as
Recalling the discussion on the limits of linearization in the previous section, we can now write the solutions for the point-like test particles as
where we introduced two characteristic length scales, the electrostatic Bjerrum length
and an elastic characteristic length given by
Note the electrostatic-elastic analogy in the definition of both lengthscales. We get an estimate for both lengths by assuming an aqueous solvent
ϵ =
ϵrϵ0 ∼ 78
ϵ0 with
ℓB ∼ .7 nm, and a colloidal crystal bulk modulus (
λ + 2μ) ∼ 100 dyne/cm
2 implying that
if
v0 is in nm. Consequently
ℓE and
ℓB would be comparable for
v0 being a fraction of a colloid lattice unit cell of ∼μm lattice spacing. In this case, the validity of the linearization ansatz can then be expressed as (
κℓB)
α(e
−κa)/(
κa) < 1, which implies also
, where
a would correspond to an effective core radius of the interstitial test particle.
We next calculate the total interaction energy between two otherwise identical point-like test sources with the same electrostatic charge and elastic ‘charge', one located at
x1 and the other one at
x2, with ∣
x1 −
x2∣ =
D. From the total free energy and taking into account the linearized mean-field equations, equation (
19), we obtain
which can be evaluated explicitly. Note that
ρe,
φ and
u refer to the sum of all the source(s) and all the field(s) and thus necessarily contain also the self energies; however, we will be interested only in the part that depends on the separation
D between the sources. Using the second equation in equation (
19) we derive equation (
29) in the final form
For non-zero
ξ, it follows from its definition that
α ≥ 1, while the decay length is obviously smaller (shorter-ranged) than the bare Debye length,
κ ≥
κ0. This follows from the fact (see section
4) that the inverse square of the screening length is proportional to the charge density response function. Consequently, any terms additive in free energy, like the elastic terms in our case, add to the charge density response function, thus decreasing the effective screening length.
The interaction energy
can be either larger or smaller then the standard (no background colloidal lattice) DH screened electrostatic interaction
depending on the interplay of the increased magnitude and increased screening. The electrostatic-elastic coupling thus creates a non-trivial modification of the interactions between interstitial inclusions.
4. Fluctuations around mean-field solution
Notably, the solutions of the linearized mean-field equations, as derived above, can in principle be extended to a negative value of the coupling constant α, or equivalently to imaginary screening length leading to oscillatory field solutions. Would this be real? An important issue that needs to be addressed at this point is therefore the range of validity of the mean-field solution that we derived above. The standard approach is to investigate the fluctuations around this solution, governed by the field Hessian, and to ascertain that all the eigenvalues of the Hessian are positive.
In order to assess the role of fluctuations around the mean-field (MF) solution,
δu and
δφ, we need to analyze the deviations from the mean-field solution quantified by
u =
uMF +
δu and
φ =
φMF +
δφ, where
uMF,
φMF are the solutions of the EL equations derived above. In order to proceed, we first note that the mean-field free energy equation (
10) can be cast in the form
which now contains only the field variables. Without the elastic displacement terms this free energy would correspond to the well-known alternative form of the PB free energy that contains only the mean-field electrostatic potential [
42].
The exact partition function now has to be written as a functional integral over the imaginary field
iφ [
43,
44] and the field
u. Since we are interested only in the limit of stability of the mean-field solution, we expand this field partition function to the second order in
δφ and
δu around the saddle point of the field action, corresponding to the evaluation of the field Hessian, which will fortunately turn out to be rather simple to analyze, and will consequently answer our original question on the range of validity of the mean-field theory.
Expanding the total field free energy to the second order we are then led to a deviation from the mean-field value of the free energy for the electrostatic potential and the longitudinal component of the deformation field
since the transverse component of
δu is not coupled to electrostatics. Above we introduced the derivatives of the mean-field charge density, equation (
15). As already noted, the
i in front of the term linear in
δφ stems from the functional integral representation of the Coulomb fluid partition function [
43,
44]. In addition, because of equation (
15), we have
The derivative of the charge density,
, by definition the capacitance density response function, is in fact proportional to the square of the inverse Debye screening length [
45]
The longitudinal component of the elastic displacement vector derivatives yields a Gaussian integral and can be integrated out from the partition function, yielding a purely electrostatic expression with a renormalized screening length
This of course tallies with the screening length derived from the mean-field equations.
Since the condition that the eigenvalues of the Hessian be positive is thus reduced to the condition that the screening length is real, the stability of the mean-field solution is defined by 1 − ξ ≥ 0, with strict identity corresponding to the limit of stability.
Let us investigate then the consequences of this result. From the definition of the elastic constants, equation (
4), it follows that
, where
a is the colloidal lattice spacing and the colloid–colloid interaction potential was assumed to be short-ranged. The strength of this interaction potential depends on the colloidal charge, which cannot be measured directly [
35]. Taking instead the measured colloidal crystal bulk modulus (
λ + 2
μ) ∼ 100 dyne/cm
2, the regime of
ξ ≤ 1 holds if
β″(
a) ≪ 1/
a2 and
n0 ≪ 1/
a3. If, on the other hand, these criteria are not satisfied and the colloidal crystal is strongly charged, the mean-field would cease to be a valid description and, following the general analogy with Coulomb fluids [
46], one would need to formulate a strong coupling theory for this problem.
Based on the above analysis, the applicability of the mean field theory is therefore limited by the requirement that
ξ ≤ 1, which can be reduced to
while the validity of the linearization ansatz, equation (
18), together with the solution of the linearized equations, equations (
25) and (
20), can be expressed as
where
b would correspond to an effective core radius of the interstitial test particle. Clearly, assuming
ξ ≪ 1, so that mean field is valid, implies that the linearization of the mean field equations is also allowed if the screening length is much larger then the core radius of the colloid. Assuming the values relevant to experiment [
47],
b ∼ .1
μm,
a ∼ 1 − 4
μm, and the effective salt concentration estimated from the dissociation of the colloidal particles to be below ∼
μM, both above conditions are satisfied.
As we noted above, outside the stable regime of parameter values the MF solutions would formally acquire a periodic component, perhaps indicating a delocalized-to-localized transition in the mobile ion density. It remains to be explored either within a strong-coupling framework or in detailed simulations that fully include the electrostatic interactions.
5. Results and discussion
We now analyze the general results derived above for the electrostatic field and elastic displacement field of a single test particle, and also the interaction between two test particles located at a finite separation, in terms of the parameters of the model. The point-like test particles are characterized by an electrostatic charge e0 and an elastic ‘charge' v0(λ + 2μ) that are both taken as parameters of the model.
The radial component of the electrostatic field of a single point source can be cast in the form
where the radial electrostatic field
Er(
R,
ξ) can be written in a dimensionless form
as a function of variables
R =
κ0r and
. Its dependence
Er(
R,
ξ) is presented in figure
2.
Figure 2. The behaviors of the dimensionless electrostatic field , equation (39), as a function of both relevant variables R = κ0r and (inset). Clearly, the dependence on the coupling parameter ξ is non-monotonic in the inset, but the dependence on the dimensionless radial distance from the point source R is monotonic, and the decay is the fastest for the pure electrostatic system ξ = 0. |
Full size|PPT slide
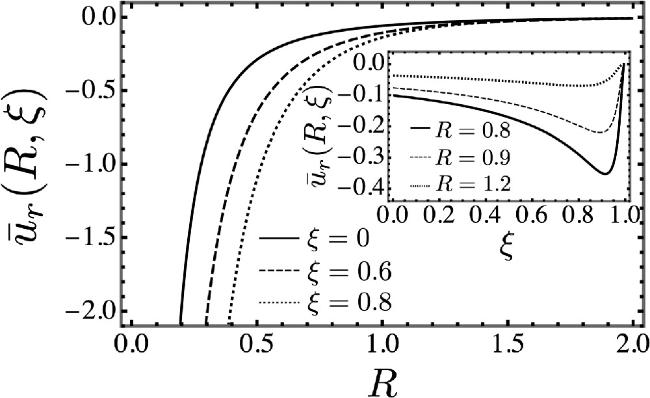
Next, we characterize the radial component of the elastic displacement of the colloidal lattice as follows
where
is a dimensionless form as a function of variables
R =
κ0r and
and quantifies the elastic displacement of the colloidal lattice induced by the electrostatic and elastic interactions. Its dependence
is presented in figure
3.
Figure 3. The behaviors of the dimensionless radial elastic displacement field , equation (40), as a function of both variables R = κ0r and (inset). Clearly, the dependence on the coupling parameter ξ is non-monotonic, while the dependence on the dimensionless radial distance from the point source is monotonic, and the increase is fastest for the pure electrostatic system. |
Full size|PPT slide
We finally analyze the consequences of the electrostatic-elastic coupling on the interaction free energy, equation (
29), between two test particles characterized by the same
e0,
v0 but located
D apart. Comparing the lattice-mediated electrostatic interaction with the standard DH interaction, we write the result in the following form
where
, and
, the relative change with respect to the DH interaction, can be cast into a dimensionless form as a function of dimensionless variables
and
ξ, quantifying the relative change in the DH interaction energy due to electrostatic-elastic coupling. It can be either positive,
, corresponding to repulsive elastic coupling-induced interactions, or negative,
, corresponding to attractive elastic coupling-induced interactions, dependent on both the coupling strength
ξ and the distance
D.
In order to understand the phase diagram better, we take the logarithm of both sides of
to further obtain
Let
, then the above equation can be rewritten as
With
ξ approaching 0,
δ also approaches 0 and
thus goes to a universal ‘critical' constant
, which does not depend on any parameters or variables (see the green dot indicated by an arrow in figure
4).
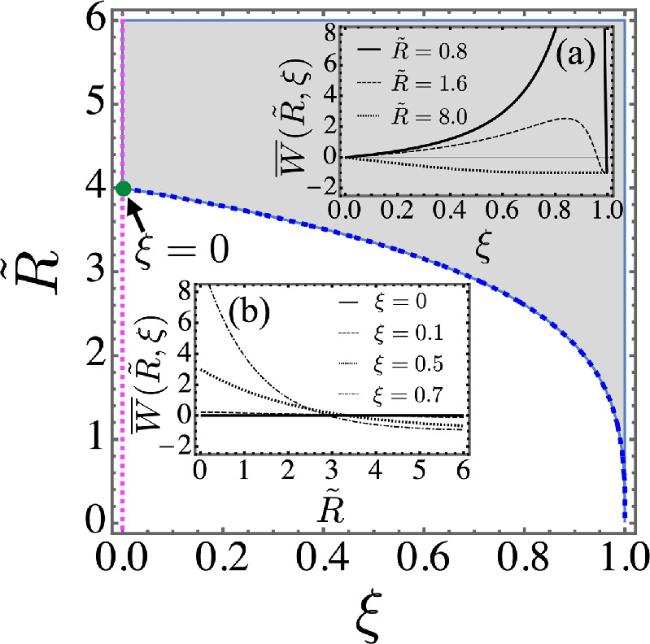
Figure 4. Behaviors of the dimensionless total electrostatic-elastic coupling free energy , equation (41), as a function of both variables and . Under a moderate dimensionless distance , the dimensionless total energy shows a non-monotonic dependence on the electrostatic-elastic coupling parameter ξ, but at large enough distance , it changes to a monotonic decaying dependence on the coupling parameter ξ and the interaction is purely attractive (Inset (a)). The smallest attainable value of is obviously −1, which corresponds to the vanishing of the electrostatic-elastic coupling interaction, with the attractive contribution compensating the repulsive contribution. But the dependence on the dimensionless radial distance from the point source is decreasing, and decaying is slower as the electrostatic-elastic coupling constant is weaker. Finally, it vanishes for the pure electrostatic system ξ = 0 (Inset (b)), and the ‘phase diagram' in the parameter space delineates a repulsive region in an otherwise attractive sea. The magenta dotted line shows our theory goes back to the standard DH theory for the coupling strength ξ = 0. The blue dashed line indicates a ‘critical line' as a function of ξ separating the repulsive and attractive regions. A universal ‘critical' constant is indicated by a arrow for ξ = 0. |
Full size|PPT slide
Inset (a) in figure
4 displays the dependence of
on
ξ for different values of
. Clearly
corresponds to additional electrostatic-elastic coupling-generated interactions, apart from and on top of the usual DH interactions.
indicates that there are no interactions, so the DH repulsion is completely compensated by the additional electrostatic-elastic coupling interaction.
implies additional interactions that are repulsive and
corresponds to additional attractive electrostatic-elastic coupling interactions that, however, do not overpower the underlying DH repulsion.
starts off at zero at
ξ = 0, and then depending on
either develops a local negative minimum
, for
, or spikes into a local positive maximum for
until again settling down at
for
ξ = 1. Furthermore, as can be seen from figure
4,
is possible only for
, which represents in some sense a ‘critical line'
as a function of
ξ of the electrostatic-elastic coupling interaction, separating a regime of
from
. For
,
corresponds to a regime where the electrostatic-elastic coupling contributes a purely attractive additional interaction for all values of
ξ.
Inset (b) in figure
4 displays a monotonic dependence of
on
for different values of
ξ. Clearly,
decays exponentially, but depending on
ξ it can show a regime where the electrostatic-elastic coupling contributes a purely repulsive additional interaction for small
, reverting invariably to an attractive regime of additional interaction for large enough
. In addition, the larger
ξ is, the faster is the decay of the additional electrostatic-elastic coupling-generated interaction. The screening length can be in fact much smaller then the Debye length, so the electrostatic-elastic coupling effect can be short-range.
A simple continuum model of electrostatic-elastic coupling between small, mobile ions and a fixed colloidal lattice, based on the mean-field electrostatic energy and Hookeian elasticity, coupled by minimal coupling terms and solved in the linearized mean-field framework, can thus lead to an attractive additional component in the overall interaction between two test particles in the colloidal lattice. While this lattice-mediated interaction evaluated on the mean-field level cannot overpower the underlying electrostatic repulsion between charges, it can effectively eliminate it, i.e. when . On the level of this theory, the electrostatic-elastic coupling can thus substantially diminish the repulsion between two mobile charges but cannot completely reverse its sign.
Our approach is necessarily approximate and model-dependent, as such being open to generalizations in different directions. While the continuum elastic lattice approximation allows for straightforward analytical developments, the connection between the colloid–colloid interaction potential (∣
ri −
rj∣), see equation (
3), and the interstitial Coulomb fluid is not direct, requiring an additional, even if very reasonable, assumption that it is of a screened Coulomb type. Note also that the colloid–colloid interaction potential depends on the assumed value of the dissociated charge of the colloids, which can include the effects of distorted double layers at high macroion volume fractions, but it is also difficult to disentangle from experiments and even more from a detailed calculation based on explicit charge dissociation models [
45]. Using the phenomenological elastic constants as opposed to phenomenological effective colloidal charges seems in our view more appropriate and going beyond would necessitate a different formulation that would loose the intuitive clarity of the Hookeian elasticity.
There are two obvious generalizations that one could pursue in a more detailed description of this system. The first one would be to alter the model and bypass the continuum Hookeian lattice approximation. Instead one would consider explicit finite-size colloids on a lattice and solve the PB equation in the interstitial space with the proper boundary conditions [
11,
36], possibly including also charge regulation [
45] at the surface of the macroions. While this could allow for a more detailed inclusion of the finite-size effects [
48], the theory would have to be formulated differently possibly lacking a direct connection with Hookeian elasticity.
The next step could be to go beyond the mean-field approximation. As the colloids are strongly charged, the colloidal crystal can certainly be conceived as a strongly coupled electrostatic system in the strict sense of the weak–strong coupling dichotomy [
15]. The strong coupling in this context refers to the coupling between mobile ions and the lattice colloids, and the putative extension of our theory would then follow the very same pathway as in the standard strong-coupling formalism [
18]. It seems reasonable to expect that on the level of the strong-coupling theory one would end up with a net attraction between test particles, but with possibly even more complicated condensed structures of mobile charges within a fixed, charged colloidal lattice. Only after the electrostatics is properly included and modeled, the simulation as the comparison with our theory makes sense. In addition, it would be interesting to compare not only the relative probability of tracer pairs in the background colloid lattice, but an actual interaction potential that could then be compared directly with equation (
41).
Finally, our theory proposes a new mechanism for generating effective attractive interactions between equally charged ions in a colloid crystalline lattice that stems from the coupling between electrostatics and lattice elasticity, proposing a new mechanism that could prove to be important for colloid physics.
{{custom_sec.title}}
{{custom_sec.title}}
{{custom_sec.content}}
 PDF(792 KB)
PDF(792 KB)


 PDF(792 KB)
PDF(792 KB)

 PDF(792 KB)
PDF(792 KB)
 ,
,  ({{custom_author.role_en}}), {{javascript:window.custom_author_en_index++;}}
({{custom_author.role_en}}), {{javascript:window.custom_author_en_index++;}}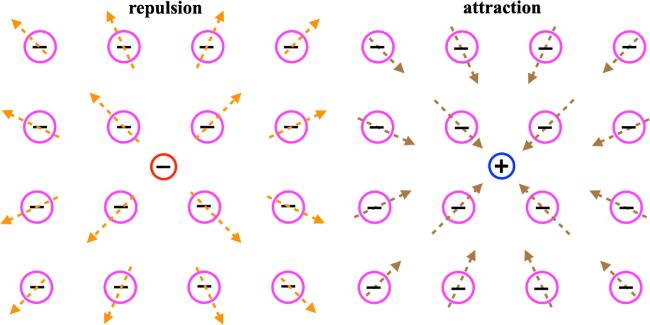


 PDF(792 KB)
PDF(792 KB)
 Figure 1. A colloidal lattice contains an interstitial charged ‘intrusion'. A negative (red circle) or positive (blue circle) interstitial test charge imposes a local elastic dilation (orange arrow) or contraction (brown arrow) on the ideal negatively charged colloidal crystal lattice (magenta circle). The interstitial charge therefore induces a local change in volume/density of the lattice.
Figure 1. A colloidal lattice contains an interstitial charged ‘intrusion'. A negative (red circle) or positive (blue circle) interstitial test charge imposes a local elastic dilation (orange arrow) or contraction (brown arrow) on the ideal negatively charged colloidal crystal lattice (magenta circle). The interstitial charge therefore induces a local change in volume/density of the lattice. Figure 2. The behaviors of the dimensionless electrostatic field
Figure 2. The behaviors of the dimensionless electrostatic field  Figure 3. The behaviors of the dimensionless radial elastic displacement field
Figure 3. The behaviors of the dimensionless radial elastic displacement field  Figure 4. Behaviors of the dimensionless total electrostatic-elastic coupling free energy
Figure 4. Behaviors of the dimensionless total electrostatic-elastic coupling free energy