1. Introduction
2. The symmetric BCQT protocol for two-qubit states
Table 1. The expressions for $| {f}_{{p}_{1}{q}_{1}{p}_{2}{q}_{2}}^{l}\rangle $ and the recovery operations (RO). |
| p1q1, p2q2 | l | p1q1, p2q2 | l | $| {f}_{{p}_{1}{q}_{1}{p}_{2}{q}_{2}}^{l}\rangle $ | RO |
|---|---|---|---|---|---|
| 00,00 | 0 | 10,10 | 1 | α0∣00⟩ + α1∣01⟩ + α2∣10⟩ + α3∣11⟩ | I ⨂ I |
| 00,01 | 0 | 10,11 | 1 | α0∣01⟩ + α1∣00⟩ + α2∣11⟩ + α3∣10⟩ | I ⨂ X |
| 00,10 | 0 | 10,00 | 1 | α0∣00⟩ − α1∣01⟩ + α2∣10⟩ − α3∣11⟩ | I ⨂ Z |
| 00,11 | 0 | 10,01 | 1 | α0∣01⟩ − α1∣00⟩ + α2∣11⟩ − α3∣10⟩ | I ⨂ (ZX) |
| 01,00 | 0 | 11,10 | 1 | α0∣10⟩ + α1∣11⟩ + α2∣00⟩ + α3∣01⟩ | X ⨂ I |
| 01,01 | 0 | 11,11 | 1 | α0∣11⟩ + α1∣10⟩ + α2∣01⟩ + α3∣00⟩ | X ⨂ X |
| 01,10 | 0 | 11,00 | 1 | α0∣10⟩ − α1∣11⟩ + α2∣00⟩ − α3∣01⟩ | X ⨂ Z |
| 01,11 | 0 | 11,01 | 1 | α0∣11⟩ − α1∣10⟩ + α2∣01⟩ − α3∣00⟩ | X ⨂ (ZX) |
| 10,00 | 0 | 00,10 | 1 | α0∣00⟩ + α1∣01⟩ − α2∣10⟩ − α3∣11⟩ | Z ⨂ I |
| 10,01 | 0 | 00,11 | 1 | α0∣01⟩ + α1∣00⟩ − α2∣11⟩ − α3∣10⟩ | Z ⨂ X |
| 10,10 | 0 | 00,00 | 1 | α0∣00⟩ − α1∣01⟩ − α2∣10⟩ + α3∣11⟩ | Z ⨂ Z |
| 10,11 | 0 | 00,01 | 1 | α0∣01⟩ − α1∣00⟩ − α2∣11⟩ + α3∣10⟩ | Z ⨂ (ZX) |
| 11,00 | 0 | 01,10 | 1 | α0∣10⟩ + α1∣11⟩ − α2∣00⟩ − α3∣01⟩ | (ZX) ⨂ I |
| 11,01 | 0 | 01,11 | 1 | α0∣11⟩ + α1∣10⟩ − α2∣01⟩ − α3∣00⟩ | (ZX) ⨂ X |
| 11,10 | 0 | 01,00 | 1 | α0∣10⟩ − α1∣11⟩ − α2∣00⟩ + α3∣01⟩ | (ZX) ⨂ Z |
| 11,11 | 0 | 01,01 | 1 | α0∣11⟩ − α1∣10⟩ − α2∣01⟩ + α3∣00⟩ | (ZX) ⨂ (ZX) |
3. The asymmetric BCQT protocol for single- and two-qubit states
Table 2. Expressions for $| {f}_{{p}_{1}{q}_{1}}^{l}\rangle $ and the RO. |
| p1q1 | l | p1q1 | l | $| {f}_{{p}_{1}{q}_{1}}^{l}\rangle $ | RO |
|---|---|---|---|---|---|
| 00 | 0 | 10 | 1 | α0∣0⟩ + α1∣1⟩ | I |
| 01 | 0 | 11 | 1 | α0∣1⟩ + α1∣0⟩ | X |
| 10 | 0 | 00 | 1 | α0∣0⟩ − α1∣1⟩ | Z |
| 11 | 0 | 01 | 1 | α0∣1⟩ − α1∣0⟩ | ZX |
4. The universal BCQT protocol
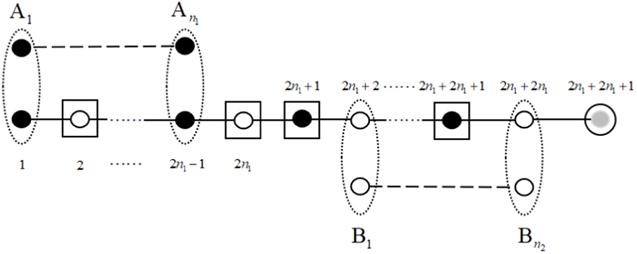
Figure 1. Process of our universal BCQT protocol. Black solid points represent Alice's particles, white points represent Bob's particles, and the gray point represents Charlie's particle. The dotted ellipses indicate Bell-state measurements, and the solid circle is a single-qubit measurement. The solid rectangle indicates the recovery operation. |
5. Discussion and comparisons
Table 3. Comparison of the symmetric protocol for two-qubit states (n1 = n2 = 2). |
Table 4. Comparison of the asymmetric BCQT protocol for single- and two-qubit states (n1 = 1, n2 = 2). |
| Protocol | QC | BO | CCC | NQT | η |
|---|---|---|---|---|---|
| [20] | 8-ES | UO, BSM, FQM, TQM, RUO | 8 | 3 | $\tfrac{3}{16}=18.75 \% $ |
| [21] | 7-ES | BSM, SQM, CNOT, RUO | 7 | 3 | $\tfrac{3}{14}\approx 21.43 \% $ |
| [22] | 7-ES | BSM, SQM, RUO | 7 | 3 | $\tfrac{3}{14}\approx 21.43 \% $ |
| [23] | 7-ES | BSM, SQM, RUO | 7 | 3 | $\tfrac{3}{14}\approx 21.43 \% $ |
| [24] | 7-ES | BSM, SQM, RUO | 7 | 3 | $\tfrac{3}{14}\approx 21.43 \% $ |
| Ours | 7-ES | BSM, SQM, RUO | 10 | 3 | $\tfrac{3}{17}\approx 17.65 \% $ |
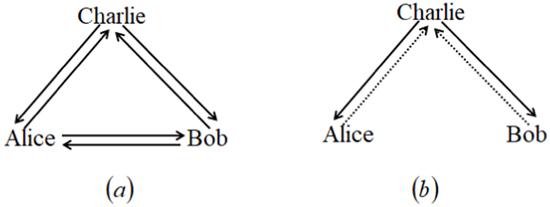
Figure 2. Classical channel models. (a) The usual model; (b) our model. A solid line with one arrow denotes a one-way broadcast channel, while a dotted line with one arrow denotes a one-way classical channel. |