Sr₂RuO₄ has drawn significant attention due to its unique electronic properties, including its unconventional superconductivity, anisotropic transport properties and non-trivial topology [1–3]. The underlying physics of these properties has been the focus of numerous experimental and theoretical studies [4].

Experimental studies have played a pivotal role in elucidating the electronic properties of Sr₂RuO₄. For example, measurements of the specific heat, resistivity and thermal conductivity have provided important information about the electronic and thermal transport properties of this material [5, 6]. In addition, studies of its magnetic behavior, such as the observation of a small magnetic moment, have led to the development of theoretical models aimed at explaining the origin of magnetism [7]. Theoretical studies based on density functional theory (DFT) have also been critical in advancing our understanding of the electronic properties of Sr₂RuO₄ [8]. DFT is a powerful tool for predicting the electronic structure of materials and investigating their properties. In the case of Sr₂RuO₄, DFT calculations have been used to predict its electronic band structure and Fermi surface, which are important for understanding its electronic properties [9]. Furthermore, DFT calculations have been used to study the effects of external perturbations, such as strain and doping, on the electronic properties of Sr₂RuO₄ [10].

The concept of the deformation potential theory (DPT) has emerged as a powerful tool for understanding the electronic properties of Sr₂RuO₄ [11]. Deformation potential is a measure of the change in energy of a band due to deformation of the crystal lattice. This theory has been used to explain the unusual anisotropic transport properties of Sr₂RuO₄, as well as its superconductivity [12]. Specifically, it has been suggested that the superconductivity in Sr₂RuO₄ arises from an odd-parity spin-triplet pairing mechanism [13], which is intimately connected to the lattice deformation. Recent developments in experimental techniques, such as scanning tunneling microscopy and angle-resolved photoemission spectroscopy, have allowed for direct measurement of the electronic properties of Sr₂RuO₄, providing new insight into its underlying physics [14]. For example, these techniques have revealed the presence of chiral p-wave superconductivity, which is consistent with the theoretical predictions based on the DPT [15, 16]. The combination of experimental and theoretical studies has led to significant progress in understanding the electronic properties of Sr₂RuO₄ [17]. The concept of the DPT has emerged as a powerful tool for explaining the unique electronic properties of this material, and its relationship with the observed superconductivity and anisotropic transport properties has been extensively investigated [18]. Further studies of Sr₂RuO₄ are likely to provide new insight into the physics of unconventional superconductivity and topological materials [19, 20].

This scientific paper focuses on the investigation of the uniaxial absolute deformation potentials (ADPs), which are fundamental physical properties that describe the relationship between uniaxial strain and shifts of individual band edges. These deformation potentials are critical for various applications, such as determining natural band offsets between mismatched material systems and understanding electron–phonon interactions. The paper is structured in a meticulous manner, with section 2 providing a comprehensive overview of the geometric and electronic properties using DFT. Section 3 elucidates the uniaxial deformation potentials and the associated computational methods. Section 4 discusses the Voigt–Reuss–Hill (VRH) approximation method and its use in evaluating the mechanical properties of materials. Section 5 explores the role of acoustic phonons in Sr₂RuO₂F₂, a quaternary alloy semiconductor with potential applications in developing accurate transport property models. Section 6 examines the intrinsic resistivity of Sr₂RuO₂F₂, a conductive material, and how it is affected by factors such as charge carrier type and mobility. The final section summarizes the key findings and provides a forward-looking perspective. Overall, this paper offers valuable insight into the uniaxial ADPs and their implications for various scientific and technological applications.

The electronic band gap of a crystalline solid is the decisive factor in classifying it as a metal, semiconductor or insulator. Simulating electronic properties, especially for semiconductors, is crucial to understanding their physical behavior, which regulates their transport characteristics. Nonetheless, substituting techniques and strain engineering are extremely promising processes for enhancing the physical features of a target compound, expanding semiconductor applications and boosting thermoelectric devices.

The foregoing findings are intended to reflect the purpose of the present research. In fact, Ruddlesden–Popper-type superconductor Sr₂RuO₄ was refined as a tetragonal crystal with the space group I4/mmm (N°. 139). It consists of alternating monolayers stacked along the c-axis, as is evident from its layered crystal structure (see figure 1). As expected, based on static calculations, the relaxed state parameters attained using the generalized gradient approximation (a = b =3.84 Å; c = 12.78 Å) are congruent with earlier theoretical reports as well as experimental findings [21–23]. The electronic properties of Sr₂RuO₄ along the high-symmetry direction were investigated through the equilibrium lattice parameters via the Yukawa screened hybrid functional and spin–orbit (SO) coupling. Formally, the SO effect is still prevalent and yields adjustments to the total energy and its derivatives. As inner-shell electrons are drawn closer to the nucleus, their kinetic energy rises, and relativistic effects become crucial. In fact, the strength of the SO coupling increases quickly with the atomic number Z. For light elements, it is frequently possible to ignore or approximate using the scalar relativistic parts of the Dirac equation [24]. Nevertheless, even with only light elements, the SO interaction can effectively describe some physical properties [25]. In the second row, for heavier elements and transition metals, to some extent, the SO effect becomes important for structural and dynamical features. Meanwhile, Yukawa screening has been shown to be more successful in predicting band gaps of materials due to its screened Coulomb exchange interaction [26]. This is the inherent reason that SO coupling and hybrid functional were applied in the present scientific report. As illustrated in table 1, our outcomes notably exhibit a zero gap, and the combined contributions of the YS-PBE0 approach and SO coupling suggest a metallic ground state of Sr₂RuO₄. These results are fully consistent with other theoretical discoveries [27].

Extrinsic defects (i.e. doping, substituting, etc) lead to a local disturbance of the crystal lattice periodicity. A defect is described by its electronic configuration (i.e. by the wave functions ψ_i associated with bound electrons i and also by the energy levels E_i of these electrons) and atomic configuration, including the distortions of the surrounding crystal lattice. The study of point defects is usually paramount. The presence of imperfections is typically regarded as an efficient means to enhance the physical features of a target compound, especially the electronic and transport properties. The electronic behavior can be deduced, at least in principle, from the electronic structure (ψ_i, E_i), and this was the aim of our research. From the relevant literature, we highlighted the studied compound. The fractional atomic coordinates of the two non-equivalent oxygen atoms were defined as follows: O ₍₁₎: 4c (0, 0.5, 0) and O ₍₂₎: 4e (0, 0, 0.1607) [28]. The strontium and ruthenium reside in Sr: 4e (0, 0, 0.3527) and Ru: 2a (0, 0, 0), respectively. Our findings suggest that the least total energy was produced when substituting oxygen atoms with fluorine atoms at O ₍₁₎ sites (i.e. creating point defects), thus being energetically the most advantageous. Volume–energy optimization was performed to ascertain the structural stability of unconstrained Sr₂RuO₂F₂ using Murnaghan’s equation of state [29]. Under free conditions, the tetragonal symmetry of the primitive unit cell persists despite the embedding of fluorine atoms. Somehow, the proposed substitution pushes the bands and electronic states from the Fermi level to lower energy levels, creating a forbidden region, where the density vanishes, as depicted in figure 2.

The electronic relocation was systematic, due to the electronic amendment and enhancement of interaction intensities between atoms after doping. This led to the widening of the energy gap in both the majority and minority spins. The upper part of the valence band and the bottommost of the conduction band are inclined at different symmetry points, attributed to an indirect band gap of the material (see figure 3).

For instance, several physical quantities, notably the band locations, were strongly affected by the choice of functional. Indeed, the band gap for Sr₂RuO₂F₂ at the YS-PBE0 level of theory (1.586 eV) showed a slight mismatch when SOC was applied (1.518 eV), as quantified in table 1. Since ruthenium (Ru) is a heavier element than strontium (Sr) and oxygen (O), it was expected that Ru would exhibit stronger SOC. However, the incorporation of SOC terms had no discernible effect on the primary electronic features, such as the electronic band gap. This proves that ruthenium is not ‘heavy enough’ to induce qualitative changes. Nonetheless, we have taken full SOC effects into account when calculating the band structures and electronic band gaps. Under free conditions, the SO separation energy was exceptionally small, as illustrated in figure 4. We attribute this smaller value to the minor effect of the nuclear charge (Z_eff) of the Ru atom and the weak variation of the charge gradient in an elementary crystal system such as Sr₂RuO₂F₂. Nonetheless, the SOC effect is greatest in the conduction band due to the orbital composition of these bands, which is typically contributed by heavy atoms (such as ruthenium). In the following, strain engineering was quantitatively applied along the c-axis, which significantly affects the electronic features in Sr₂RuO₂F₂. For convenience, we replicated a compressed and expanded region of the same material, which is clearly visible in figure 3.

The semiconducting behavior persists, and so a linear relationship was observed between the external strain and the corresponding bandgap values (see figure 2). Stretching provides effective tunability in the band gap and returns it to 1.75 eV at ϵ_z = + 0.08. The bandgap energy folds back to 1.15 eV at ϵ_z = −0.08 upon spreading the compressive strain. The outcomes obtained from the YS−PBE0 method were fairly homogeneous and proportional to those obtained from YS−PBE0 + SOC. The effective electron mass ratio and the effective masses of holes can be readily calculated from the band structure using the formula ${m}^{* }={\overline{h}}^{2}{\left({\partial }^{2}\,E\left(K\right)/\partial {K}^{2}\right)}^{-1}$ [29]. In the equilibrium state (i.e. unstrained Sr₂RuO₂F₂), the topmost valence bands exhibit heavy masses, which are detrimental to their mobility. The mass of the upper valence band is as low as ≃9.10⁻³¹Kg and falls continuously in the compressed region, as shown in figure 5. In contrast, the pressure pushes the electron effective masses upwards to a value of ≃ 1.75.10⁻³¹Kg and a huge increase was witnessed. Neither experimental nor theoretical findings are currently available for comparison. Nonetheless this discovery yields a theoretical prediction, which ought to fill a gap and contribute to new research.

In an attempt to explain the interaction between electrons and acoustic phonons and to circumvent this problem, Bardeen and Shockley [30] introduced the DPT [31]. The ADP concept reflects the electron–phonon interaction and outlines the mismatch between electron energy levels in the same stretched and compressed solid. The former concept was coined to describe the strain-induced shift of one-electron energy levels in the structure [32]. Indeed, conduction and valence band displacements caused by the lattice deformations due to the sonic waves significantly affect carrier mobility. Carrier mobilities of their lathe were sketched in terms of scattering by the deformation potential. Research demonstrated that the ADPs are simple derivatives of the energies with respect to the strains by making straightforward assumptions [33] and can be defined as, where ${D}_{{i}}$ is the deformation potential of a given state i, ${\rm{\Delta }}{E}_{{i}}$ is the shift of its energy under strain and usually E_i depicts the eigenvalue of the Kohn–Sham Hamiltonian. The relative change of volume is related to the normal strains in x, y and z directions and is given by [33],For completeness, ADP is often derived from strained superlattice computations on the Sr₂RuO₂F₂ 3D semiconductor. Theoretical ascertainment of the ADPs has been fairly controversial and involves a substantial number of inspections, renditions and assumptions [34]. The uniaxial ADP highlights the long-range electrostatic effects and can be described by [33],Quantitatively, in this research, ϵ_z represents the external uniaxial strain applied along the c-axis. The conduction and valence band ADPs (${{\rm{D}}}^{{\rm{VBM}}}\,{\rm{and}}\,{{\rm{D}}}^{{\rm{CBM}}}$) allow for the direct calculation of the bandgap deformation potential [33]:

The fundamental derivatives of the band energies with respect to strains at the ground states are ADPs. The latter can only be used to predict the absolute energies of the electronic states for different strain conditions. For convenience, we will later demonstrate the correlation between band energies and strains by illustrating the linear regime of this dependence in the intrinsic case of Sr₂RuO₂F₂. To begin, we investigate the ADPs of uniaxially strained Sr₂RuO₂F₂ using the YS-PBE0 approach and SO coupling. The energies of the topmost valence band at the Λ, N and P points and the bottommost of the conduction band at the H, N and Γ positions in the Brillouin zone, as a function of strain, are listed in table 2.

The ADPs were obtained by linearly extrapolating the band energy edges as a function of axial strains, as shown in figure 6. The findings indicate that the correlation can be assumed to be linear for strains between ϵ_z = −0.08 and ϵ_z = + 0.08.

The band edge positions of Sr₂RuO₂F₂ are highly responsive to strain and evolve towards different values in a consistent manner. The valence band energies (VBM) at the N point steadily decrease in the stretched region (i.e. when the lattice parameter grows). Despite this behavior, the CBM energies at the N point progressively increase, and this trend persists even when external strain is applied (see figure 6).

Note that the change in valence and conduction states under deformation can be due to the following physical trend.

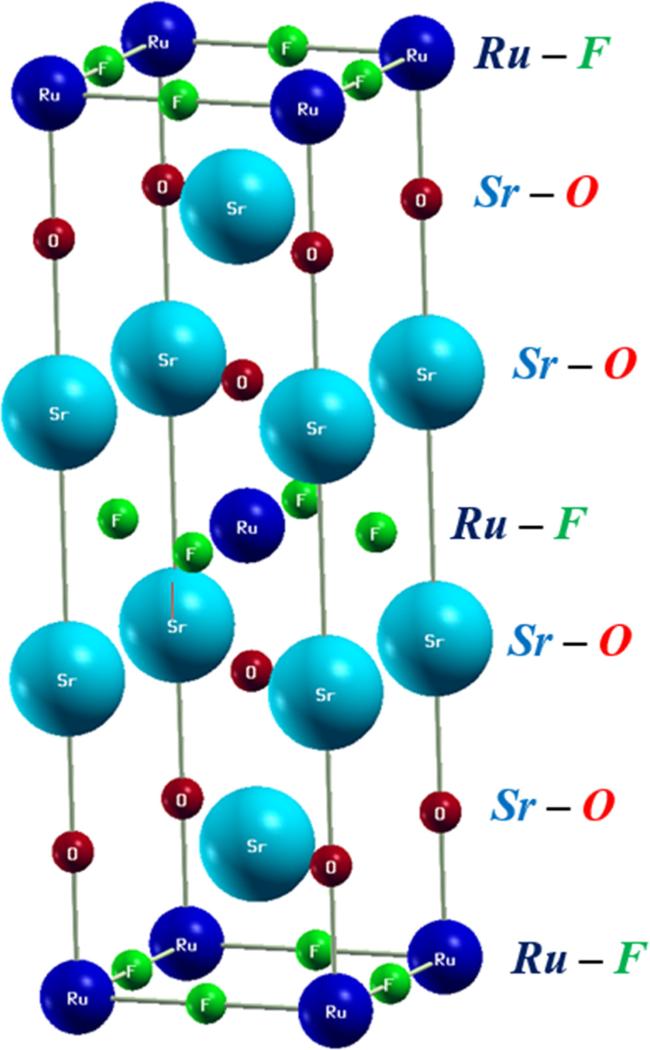
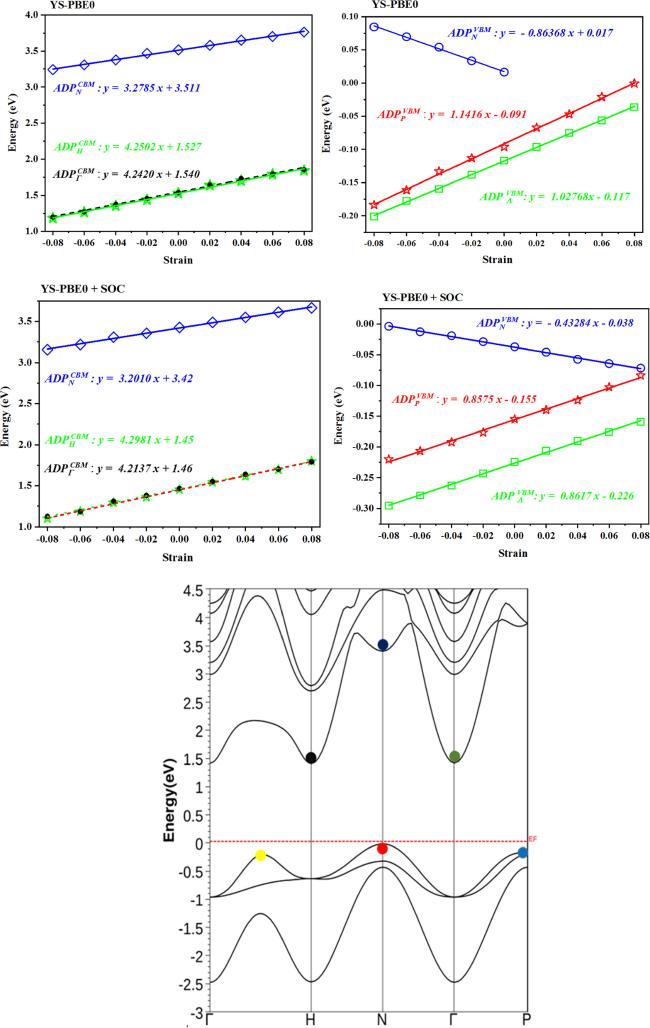
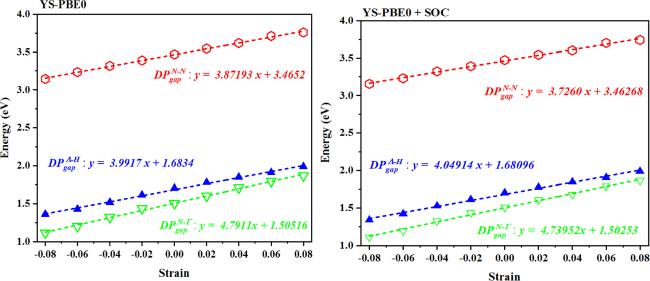
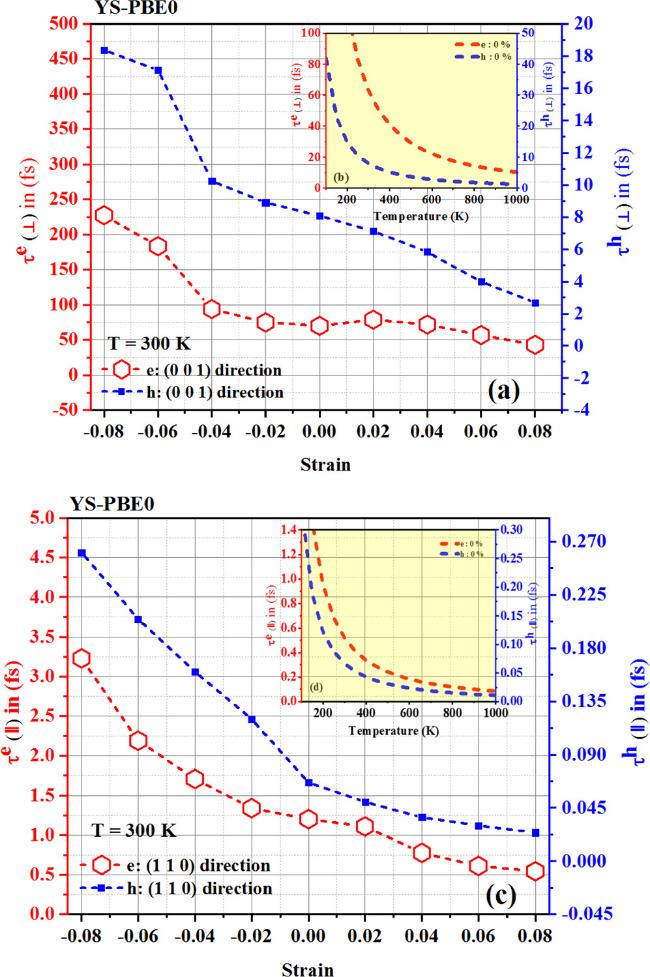
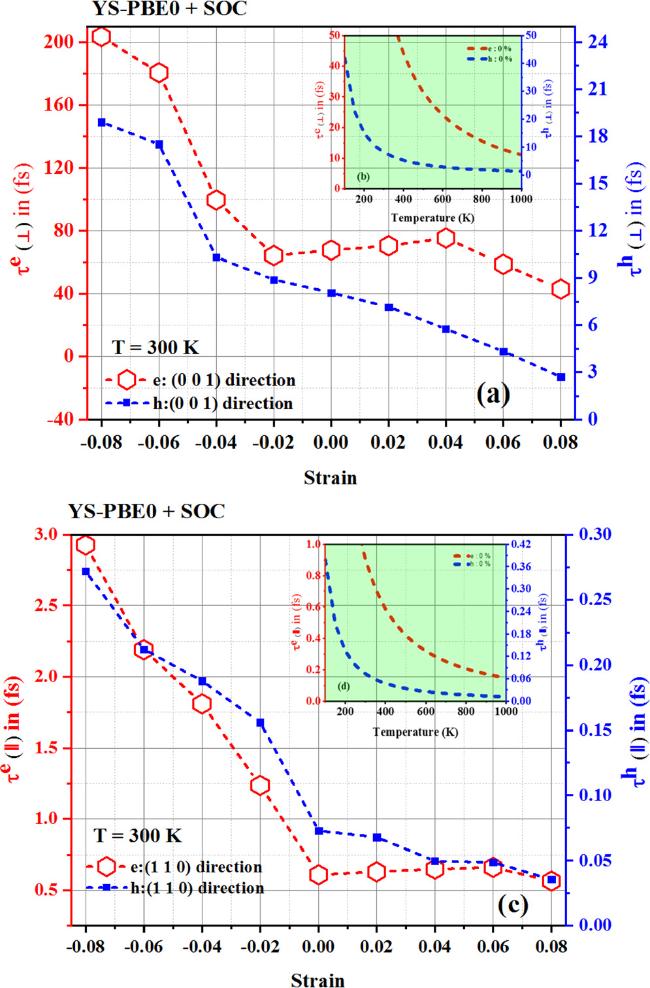
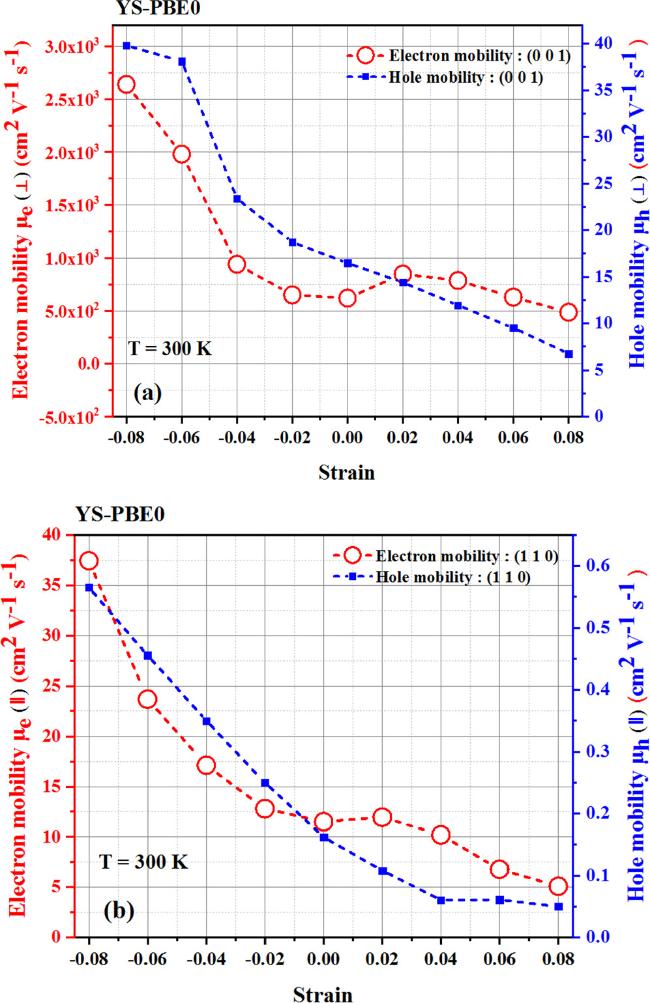
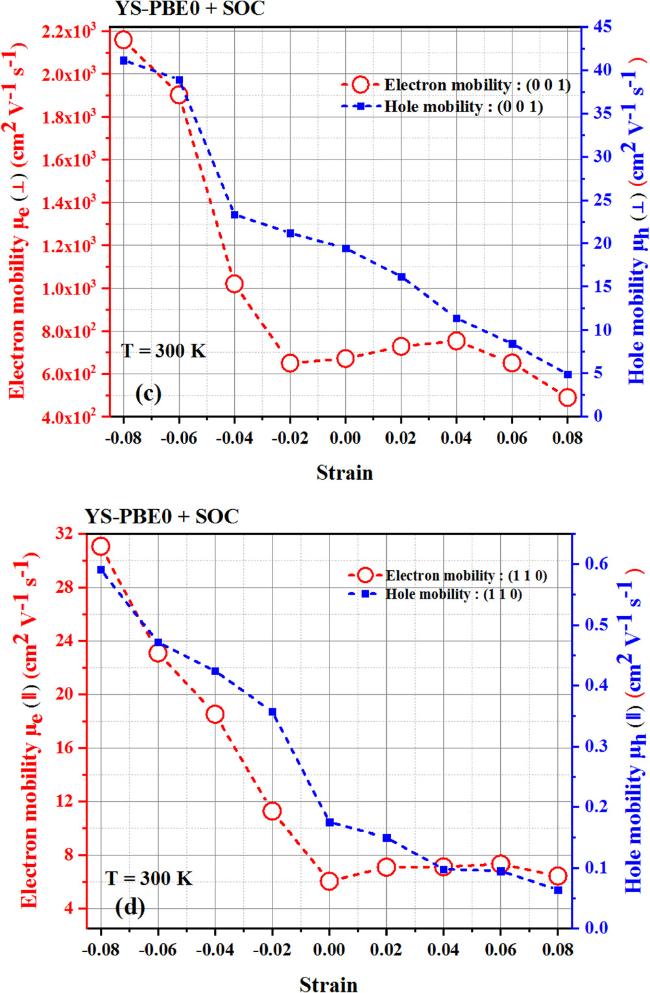
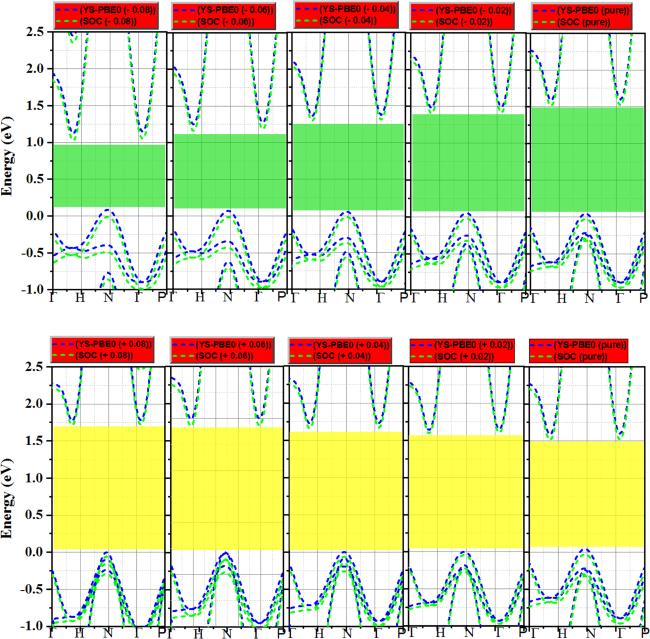
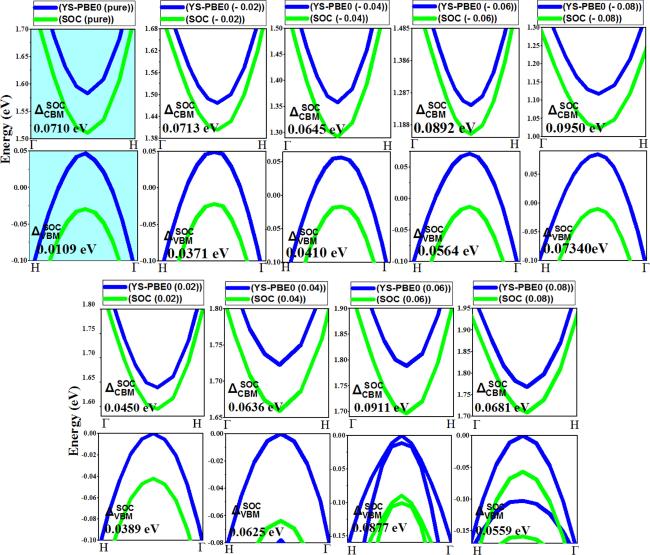
Regarding the quaternary alloy Sr₂RuO₂F₂, the state at the N point of the valence band (VBM) exhibits metal-like characteristics and has a bonding interaction with the F and O orbitals. As the alloy is expanded, the energy of this state experiences a significant decrease using both the YS-PBE0 approach and SO coupling. This is due to the fact that as the distance between atoms increases, the bond length (i.e. stretching) also increases, leading to a decrease in energy. The bonding nature of the state contributes to an increase in energy when the bond length shortens, but as the bond length increases, the energy also decreases. (see figure 6). The kinetic energy of electrons within a substance is intimately related to the motion of these subatomic particles. As the distance between atoms within a compound expands (i.e. bond length under stretch), the energy of these electrons correspondingly decreases due to the greater spatial separation between atoms. This reduction in energy is a direct consequence of the decline in the momentum of the electrons as the atoms are farther apart, and the opportunities decline in the momentum of the electrons as the atoms are farther apart, and the opportunities for interaction with the nuclei are accordingly diminished. The correlation between the potential energy of electrons in a material and the electrostatic interactions between these electrons and nuclei is a complex and fascinating phenomenon. As the distance between nuclei, otherwise known as bond length, increases, the potential energy of the electrons correspondingly rises as a result of the weakening of the electrostatic interactions. 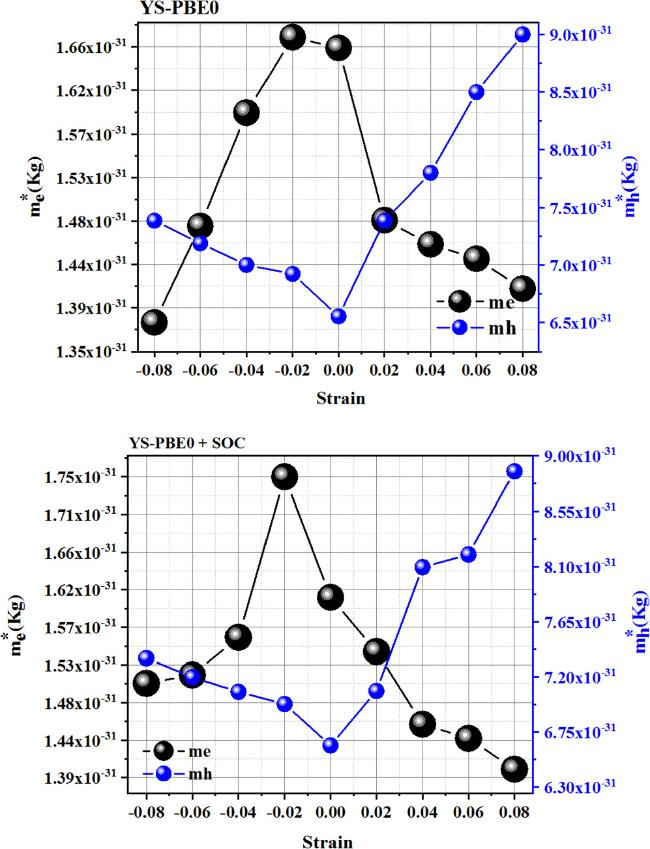This highlights the intricate interplay between the various components of Sr₂RuO₂F₂ quaternary alloy and their effect on the overall energy state. The kinetic energy of the electrons decreases at a greater rate than the increase in potential energy, resulting in a net diminution of the aggregate energy of the system. This salient phenomenon, intrinsic to the bonding state at the valence band maximum (VBM), is the very explanation for the diminutive ADP observed in table 2. In general terms, the effect of antibonding interactions on the energy edges of a material can be significant, particularly in the conduction band (CBM). As mentioned earlier, the antibonding states have a lower electron density between the nuclei, which leads to higher repulsion and increased energy. This elevation of energy can propel the state into the conduction band, thereby rendering it amenable for electrical conduction [36]. In Sr₂RuO₂F₂ semiconductor, the antibonding interactions arise from the overlap of the electronic wave functions of the Ru-4d orbitals in the RuO₂ planes with the F-2p orbitals in bonds and the electrons of the F layers. The antibonding interactions are formed between the electrons of the Ru–O and the Ru–F bonds. The Born–Oppenheimer approximation is a fundamental principle in quantum mechanics that explains the relationship between the positions of nuclei and electrons in a substance, and the resulting energy levels [37]. According to this principle, when the bond length lengthens (e.g. from ϵ_z = −0.08 to ϵ_z = + 0.08), the energy of the antibonding states at N, H and Γ points also rises, as shown in figure 6. This is because the electrons in these antibonding states, which have higher energy than the bonding states, are farther apart, resulting in higher potential energy. As illustrated in figure 6, the conduction band (CBM) electrons are more sensitive to external strains/deformations, and their energy levels change more readily in response to these changes. The energy edge is significantly affected by strain; it increased steadily under pressure/stretch and abruptly jumped to ≈3.77 eV, ≈1.87 eV and ≈1.85 eV at N, H, and Γ points respectively, when ϵ_z = + 0.08 (see figure 6). This results in the ADP being larger in the conduction band than in the valence band, as listed in table 2. The previously observed behavior persists even upon applying SO coupling.

The bandgap deformation potential, a fundamental characteristic in the assessment of the mechanical attributes of semiconductors, serves to quantitatively evaluate the alteration in the band gap of a substance in response to an imposed strain or deformation. To calculate the bandgap deformation potential of the Sr₂RuO₂F₂ quaternary alloy, a linear fit is performed on the electronic band gaps at various strains, as illustrated in figure 7. This process yields a correlation between the electronic band gap and strain, thereby enabling the computation of the bandgap deformation potential, listed in table 3. The upsurge in the gaps (${{E}}_{{\rm{gap}}}^{{N}-{\rm{\Gamma }}},$ ${{E}}_{{\rm{gap}}}^{\wedge -{H}}\,{\rm{and}}\,{{E}}_{{\rm{gap}}}^{{N}-{N}}$) under pressure/stretch is a consequence of the alteration in the electronic structure of Sr₂RuO₂F₂ brought about by the modification in the interatomic spacing. Specifically, when the Sr₂RuO₂F₂ quaternary alloy is stretched by an amount ϵ_z, the bond lengths grow, which leads to a shrinkage in the overlap between the valence and conduction bands. This reduction in overlap results in an enlargement of the band gap, perceived in figure 7, which is reflected by an escalation in the gap deformation potential (${{\rm{DP}}}_{{\rm{gap}}}$). When comparing the results obtained using the YS—PBE0 and YS—PBE0 + SO functionals, it is important to note that the two methods predict similar gap deformation potentials for the majority of cases. The significance of the gap deformation potential as a metric of the alteration in the band gap, consequent to mechanical strain, cannot be overstated. In order to comprehend the mechanical characteristics of semiconductors, it is imperative to establish a correlation between the strain and the band gap. Thus, the gap deformation potential serves as a crucial indicator in this regard.

The VRH approximation method is a widely employed technique within the field of materials science for ascertaining the mechanical properties of various materials, such as their stiffness and strength [38]. This method leverages a weighted average of the results obtained through the harnessing of the Voigt, Reuss and Hill approximations, which are based on distinct assumptions regarding the microstructure of the material in question. The implementation of this method allows for a more precise estimation of elastic properties since it takes into account the inherent heterogeneity of materials at a microstructural level, resulting in a comprehensive evaluation of the material’s mechanical features. The Sr₂RuO₂F₂ quaternary alloy, with a tetragonal crystal structure, is the subject of our extensive research regarding its mechanical properties. The stiffness matrix will be defined by the nine independent elastic constants specific to that material and crystal structure [39, 40]:Pursuant to the Born–Huang stability criteria, which are both necessary and sufficient for a tetragonal system, a structure that is mechanically sound must fulfill the following requisites [39, 40]:

The elastic constants describe the material’s ability to withstand deformation when a load is applied. The assessed elastic constants for the strained Sr₂RuO₂F₂ perovskite reveal that it is mechanically stable under strain. This can be confirmed by appraising the elastic constants against the Born criteria, as previously mentioned. The findings in table 4 reveal that all the elastic constants of Sr₂RuO₂F₂ satisfy these criteria. From the elastic constants, we can also derive various moduli that give insight into the mechanical properties of the material. The bulk modulus (B) sets forth the material’s resistance to changes in volume under pressure and can be deduced from B = (C₁₁ + 2C₁₂)/3 [40].

The calculated values of strained Sr₂RuO₂F₂ span from B_V = 288.34 GPa (ϵ_z = + 0.08) to B_V = 450.93 GPa (ϵ_z = −0.08) through YS-PBE0. Young’s modulus (E) portrays the material’s resistance to longitudinal stress and can be determined by E = 9BG/(3B + G) [40]. The large E suggests that the material is very stiff and resistant to deformation when a force is applied. Values ranging from E_V = 217.29 GPa (ϵ_z = + 0.08) to E_V = 490.02 GPa (ϵ_z = −0.08) are acquired for strained Sr₂RuO₂F₂ through YS-PBE0. The Poisson’s ratio (ν) describes the material’s tendency to expand or contract in the transverse direction when under longitudinal stress, and it can be computed with the relation ν = (3B –2G)/ (2(3B+G)) [40]. It extends from ${\nu }_{V}$ = 0.32 (ϵ_z = −0.08) to ${{\rm{\nu }}}_{{\rm{V}}}$ = 0.37 (ϵ_z = + 0.08) through YS-PBE0. The shear modulus (G) states the material’s resistance to shearing forces and can be extrapolated from G = C₄₄ [40]. G ranges from 79.05 GPa (ϵ_z = + 0.08) to 185.77 GPa (ϵ_z = −0.08) through YS-PBE0, which is related to Young’s modulus and Poisson’s ratio by G = E/2(1 + ν) [40]. The low bulk modulus and shear modulus yielded under stretch by an amount ϵ_z = + 0.08 indicate that strained Sr₂RuO₂F₂ is flexible, making it suitable for optoelectronic applications such as solar cells. The Voigt, Reuss and Hill models were all applied to estimate the elastic properties of the Sr₂RuO₂F₂ quaternary alloy, but they each make different assumptions about the behavior of the researched compound. These assumptions are based on the material’s structure and the way that it deforms under strain. For instance, the Voigt model assumes that the material is isotropic (i.e. has the same properties in all directions) and elastic (i.e. returns to its original shape after being deformed), while the Reuss model assumes that the material is isotropic and plastic (i.e. permanently deforms under strain). Since all three models make different assumptions, they yield slightly different results. However, these results are still considered to be close to each other, as listed in tables 5 and 6.

Ductile and brittle materials possess distinct features and are employed in various applications [41]. Ductile materials possess the capability to undergo plastic deformation prior to fracture, whereas brittle materials tend to exhibit sudden breakage with minimal or no plastic deformation. The mechanical properties of the strained Sr₂RuO₂F₂ quaternary alloys were evaluated employing the Pugh criteria, as outlined in table 7. This methodology entails the calculation of the Pugh ratio, obtained by dividing the bulk modulus by the shear modulus (B_H/G_H) [40]. Materials exhibiting a high B_H/G_H ratio are considered to possess ductile characteristics, whereas those with a low B_H/G_H ratio are deemed brittle. Our study reveals that the strained compounds exhibited ductile behavior, as evidenced by their B_H/G_H ratios, which were typically greater than 1.75. It is worth noting that these materials (i.e. between ϵ_z = −0.08 and ϵ_z = + 0.08 including the ground state) are relatively inexpensive and possess high strength and toughness. Our research has led to the prediction of ductile materials that exhibit exceptional strength and toughness features, making them suitable for various high-demand applications such as those found in the construction, transportation and energy sectors [42, 43]. The Cauchy relationship, also known as the Cauchy–Born rule, is a mathematical relationship that describes the deformation of a material in response to an applied strain. The relationship is represented by the equation C_c = C₁₂–C₄₄, where C_c is the compliance tensor, C₁₂ is the elastic compliance tensor and C₄₄ is the shear compliance tensor [39]. C₁₂ represents the Sr₂RuO₂F₂ ability to deform in response to a compressive or tensile strain, while C₄₄ represents its ability to deform in response to a shear strain. The difference between these two values, C₁₂–C₄₄, is a measure of the material’s ductility or brittleness. Our study on the mechanical response of strained Sr₂RuO₂F₂ quaternary alloys via the Cauchy relationship has revealed positive values of C₁₂–C₄₄ (see table 7), a clear indication of ductility.

These results indicate that these alloys are capable of undergoing significant deformation prior to failure under applied strain. These findings align with the conclusions derived from the Pugh criteria, further supporting the assertion that Sr₂RuO₂F₂ quaternary alloys possess highly desirable ductile characteristics. As such, these materials are well-suited to a broad range of engineering applications. It is worth noting that a material exhibiting a negative value of C₁₂–C₄₄ is considered to be brittle since it will fracture prior to undergoing substantial deformation under applied pressure/stretch [40, 41].

Acoustic phonons are a fundamental aspect of the physics of crystalline materials, and they correspond to the quantum mechanical excitations of the lattice vibrations [44]. In the case of the Sr₂RuO₂F₂ compound, the crystal lattice is composed of Ru, F and O atoms that are arranged in a layered structure. These phonon excitations can propagate through the lattice in a variety of directions, including along the c-axis, which is perpendicular to the layers (i.e. perpendicular direction (0 0 1)), as well as within the layers themselves (i.e. parallel direction (1 1 0)). The study of acoustic phonons in this material can provide valuable insight into its properties and behavior, and further our understanding of the underlying physics of crystalline materials. As the phonon wave propagates through Sr₂RuO₂F₂, the local lattice can undergo compression and expansion. This is due to the fact that the phonon wave is a collective motion of the atoms in the lattice, where the atoms oscillate about their equilibrium positions in phase with each other. The pressure and stretch of the local lattice leads to a perturbation of the potential energy of the bands in the crystal, and this perturbation is related to the deformation potential (e.g. in this case, the change in the potential energy of the electrons can be calculated by multiplying the deformation potential constants with the corresponding strain). The perturbation of the potential energy causes the scattering of carriers, such as electrons and holes. The scattering rate depends on the overlap of the initial and final states of the carriers, which is determined by the phonon wave’s momentum and polarization [45]. The electronic properties of the quaternary alloy Sr₂RuO₂F₂, such as electrical resistivity and mobility, can be affected by the scattering of carriers. This has been shown in subsequent sections of our research. Complementary, the phonon–electron interaction in Sr₂RuO₂F₂ can also cause the phonon-mediated superconductivity [46]. Under these circumstances, the phonons mediate the attraction between the electrons, and can lead to the formation of Cooper pairs, which are the fundamental building blocks of superconductivity [47]. The scattering rate is consistently the rate at which carriers scatter (or interact) with each other. The relaxation time is the amount of time it takes for a system to return to equilibrium after being perturbed. The two are related in that the relaxation time is inversely proportional to the scattering rate. It is arguable that if the relaxation time is known, the scattering rate can be calculated by taking the reciprocal of the relaxation time [48]. The relaxation time, represented by τ, is a crucial parameter that sheds light on the energy dissipation dynamics of carriers in semiconductor materials. The inverse proportionality between relaxation time and carrier mobility highlights the intrinsic relationship between the ease of carrier movement and the rate of energy dissipation. The order of magnitude of relaxation time in the nanosecond range for electrons and holes in semiconductors underscores its significance in determining the electrical and transport features of these materials.

The results of this study provide strong evidence for the feasibility of using the Sr₂RuO₂F₂ semiconductor in the development of a highly accurate model for transport properties. To confirm this potential, we conducted a thorough evaluation of the electronic relaxation time in both the (0 0 1) and (1 1 0) directions, by means of mathematically rigorous formulas to ensure the validity and precision of our findings [49]:

The reduced Planck constant is represented by ħ, e is the elementary charge and C_ij is the elastic matrix constant obtained by VRH approximation. For the (0 0 1) direction (⊥), C₃₃ is selected when calculating carrier mobility and electronic relaxation time. Forthe  (1 1 0) direction (∥), C₆₆ is employed. k_β is the Boltzmann constant; T is the temperature (set at 300 K) and E is the deformation potential constant, ascertained by the band edge shift with respect to the strain as previously performed. Relaxation times of carriers are illustrated at 300 K in figure 8 [(a) perpendicular direction and (c) parallel direction]. The relaxation time of holes (i.e. positively charged carriers) and electrons (i.e. negatively charged carriers), which pertains to the duration it takes for these carriers to relinquish their energy and attain a state of equilibrium within a material, was observed to be significantly longer in the perpendicular direction (${\tau }_{\perp }$) as opposed to the parallel direction (${\tau }_{\parallel }$) of Sr₂RuO₂F₂ at room temperature (ca. 300 K). This phenomenon can be attributed to the intricate interplay between the material’s electronic structure and the interaction of the holes and electrons with the crystal lattice. Being a layered compound, Sr₂RuO₂F₂ exhibits an electronic confinement of the holes and electrons primarily to the RuF layers. The longer relaxation time in the perpendicular direction implies that the carriers experience a greater difficulty in scattering and losing their energy as they traverse through the layers, as opposed to within the layers. Intuitively, these effects can be attributed to the presence of strong electronic correlations within the material, which enhance the stability of the electronic states and reduce the carrier’s ability to scatter and lose energy. In reality, the unique crystal structure of Sr₂RuO₂F₂ could also play a role, as the presence of specific types of bonding or lattice defects may impact the carrier’s mobility and scattering.

The modulation of the relaxation time in Sr₂RuO₂F₂ under external strain is the result of its intricate crystal structure and complex inter-atomic interactions (i.e. covalent bonding, electrostatic forces and electron transfer) between Ru-d, F-p, Sr-p and O-p orbitals.

The Sr₂RuO₂F₂ quaternary alloy is defined by the presence of ruthenium ions occupying a Ru⁺⁴ oxidation state, which participate in forming strong covalent bonds with the O⁻² oxidation state oxygen ions. These covalent bonds lead to the establishment of a robust crystal lattice. Fluorine, as a highly electronegative element, also plays a crucial role in determining inter-atomic interactions through its participation in electrostatic bonds. The Sr atoms provide stability to the lattice through the formation of ionic bonds with the oxygen ions. Strain induces changes in lattice dimensions, leading to alterations in the magnitude of these inter-atomic interactions and phonon scattering processes.

Upon tensile strain, the lattice expands, resulting in a reduction of scattering and a consequent acceleration of the relaxation rate, shortening the relaxation time. The relaxation periods of electrons and holes in the taut zone of (001) and (110) Sr₂RuO₂F₂ shorten as strain magnitudes alter. In the case of (001) Sr₂RuO₂F₂, the electron relaxation time fell from 70 to 41 fs and hole relaxation time underwent a reduction from 8 to 2.5 fs as ϵ_z progressed from ϵ_z = + 0.00 to ϵ_z = + 0.08. Analogously, in the instance of (110) Sr₂RuO₂F₂, the electron relaxation time was curtailed from 1.3 to 0.5 fs, while the hole relaxation time went from 7.10⁻² to 2.10⁻² fs as ϵ_z regressed from its unrestrained state to + 0.08. Conversely, compressive strain leads to lattice contraction, which enhances inter-atomic interactions and scattering processes, slows down the relaxation rate, and extends the relaxation time in both perpendicular and parallel directions. The fluctuations seen in figures 8 and 9 are correlated with alterations in the rate of phonon scattering within the crystal lattice, which is related to the type of inter-atomic interactions and the scattering process. The SOC manifests itself in a manner that is congruent with that of the hybrid functional approach (YS-PBE0) due to the fact that both methods incorporate the interactions between electrons and account for the relativistic impacts on the electron configuration. This assertion is substantiated by the graphical representation of the data (see figure 9). When scrutinizing the relationship between temperature and relaxation time in Sr₂RuO₂F₂ (as depicted in figures 8 and 9), it becomes evident that this material is progressively exhibiting a higher degree of thermal excitation and a diminished resistance to alteration. This phenomenon is a result of the interplay between thermal energy and fluctuations within the Sr₂RuO₂F₂ quaternary alloy, which excites its electrons and renders them more susceptible to alterations in their surroundings. The discernible decrease in relaxation time in both the perpendicular and parallel directions serves to underscore the material’s intensifying thermal activity, thus leading to a more expeditious reversion to a state of equilibrium.

A comprehensive study of electron scattering in semiconductors has illuminated the critical relationship between the mobility of carriers, including electrons and holes, and their effective mass and relaxation time, which are intricately tied to the interactions between the carriers and lattice vibrations. To advance our knowledge of transport properties, we propose an analytical framework that delves into the mobility of electrons and holes in both perpendicular (⊥) and parallel (∥) orientations. This framework is intended to isolate the intrinsic properties of the carriers [50], providing a more nuanced and sophisticated understanding of the underlying transport properties. Our research constitutes a valuable addition to the growing body of knowledge in the field of semiconductor physics and further advances our understanding of this complex and multifaceted phenomenon. The alteration in the mobility of charge carriers in Sr₂RuO₂F₂ observed through DFT and DPT calculations can be attributed to a complex interplay of multiple mechanisms in condensed matter physics [51]. Electron and hole mobility was significantly affected by strain in (⊥) orientation; it waned steadily under stretch and abruptly jumped to 2.60 $\times $ 10² cm² V⁻¹ s⁻¹, 39.77 cm² V⁻¹ s⁻¹ in the pressure zone at ϵ_z = + 0.08, respectively, as illustrated in figure 10. Analogously, uniaxial stretching efficiently stirred the electron transport properties in the (∥) direction.

The outcomes suggest that the tensile strain progressively curtailed the (110) relaxation times of electrons and holes and reduced their mobilities to 5.10 cm² V⁻¹ s⁻¹, 5 $\times $ 10⁻² cm² V⁻¹ s⁻¹ at ϵ_z = + 0.08, respectively. Conversely, a drastic linear upward trend in carrier mobility was noticed when the strain was lengthened from ϵ_z = −0.02 to ϵ_z = −0.08, as displayed in figure 10. Indeed, it is of the utmost significance to note that the data acquired through the YS-PBE0 approach in figure 10 exhibit a quantifiable correspondence with the results depicted in figure 11 where SOC was taken into consideration. It is evident that comparable behavior was manifested in both instances. A key factor contributing to the decline in mobility under tensile strain is the modification of the band structure of Sr₂RuO₂F₂, as previously elucidated (refer to figure 3). Tensile strain caused alterations in the density of states and effective masses of the charge carriers, leading to changes in the scattering and transport properties and a decline in mobility. In addition, tensile strain introduced lattice defects and distortions into the crystal structure of Sr₂RuO₂F₂, which serve as scattering centers for the charge carriers and reduce their mobility. The electronic correlation effects in Sr₂RuO₂F₂ can also be modified by tensile strain, leading to further alterations in the scattering and transport properties of the charge carriers. On the other hand, pressure intensifies the electron–phonon interaction. This is due to the fact that the increase in pressure can cause modifications to the electron–phonon coupling, thereby influencing the charge carrier mobility. A robust coupling can result in heightened mobility by decreasing the scattering rate of the carriers. This phenomenon highlights the delicate interplay between compression, electron–phonon coupling and charge carrier mobility in solid-state systems. Furthermore, the susceptibility of the band gap in Sr₂RuO₂F₂ is contingent upon the intricacies of its crystal lattice, which undergoes alteration upon application of compression. As previously elucidated, the pressure serves to reduce the band gap, enabling electrons and holes to traverse the material with greater ease, thus augmenting their intrinsic mobility.

Intrinsic resistivity refers to a property of a material that describes its inherent resistance to the flow of electric current. It is an intrinsic characteristic of the material itself and does not depend on the material’s geometry or shape. Intrinsic resistivity is usually known to be dependent on various factors including the type and mobility of charge carriers present in the material. In this context, it is intriguing to note that the resistivity of Sr₂RuO₂F₂ exhibits the opposite behavior as the mobilities of electrons and holes, as observed in figure 12. In conventional metals (e.g. to Sr₂RuO₄) [52], electrical conductivity is primarily governed by the high mobility of free electrons, while in semiconductors (e.g. to Sr₂RuO₂F₂), electrical conductivity is facilitated by both electrons and holes [53], with the latter characterized by lower mobility. As a result, the resistivity of semiconductors is influenced by the mobility of both charge carriers. With regard to Sr₂RuO₂F₂, there is an assumption that the perturbations inflicted upon the Fermi surface (i.e. the surface in momentum space that separates the occupied and unoccupied states) as a result of strain could potentially be undermining superconductivity. Superconductivity, a fascinating phenomenon characterized by the elimination of electrical resistance and the attainment of perfect conductivity below a critical temperature, could be hindered if the strain impinges upon the Fermi surface in a manner that hinders the essential prerequisites for superconductivity to transpire. A consequence of this would be the augmentation of electrical resistivity in (⊥) and (∥) orientations (see the stretch region), as illustrated in figure 12.

The research presented here focuses on various properties of the Ruddlesden Popper-type superconductor Sr₂RuO₄ and its quaternary alloy Sr₂RuO₂F₂. The electronic properties of Sr₂RuO₄ were studied using hybrid functional and SOC, which showed that the compound has a metallic ground state. Point defects, specifically oxygen substitution with fluorine, were investigated for their effects on the electronic structure, which resulted in a widening of the energy gap in both majority and minority spins. The ADPs of uniaxially strained Sr₂RuO₂F₂ were also analyzed, and the results showed that the band edge positions of the material are highly responsive to strain. The VRH approximation method was used to determine the mechanical properties of the material, and the nine independent elastic constants were found to be close to each other. Finally, the study investigated the acoustic phonons and phonon–electron interaction in Sr₂RuO₂F₂, which can cause phonon-mediated superconductivity. The electronic relaxation time of the material was found to be significantly longer in the perpendicular direction than in the parallel direction at room temperature, and the resistivity of the material was found to be influenced by the mobility of both charge carriers. The perturbations that may be inflicted upon the Fermi surface due to strain could potentially undermine superconductivity and lead to an increase in electrical resistivity in both orientations. Understanding these properties is crucial for the design and optimization of electronic devices, and further research in this area is needed.