1. Introduction
There are many ways of obtaining new integrable systems of equations such as taking the Lax representations in algebras of higher rank. In these methods we obtain real and complex valued coupled nonlinear equations which possess recursion operators and Hirota bilinear forms. There are also some other methods that use integrable systems with less number of dynamical variables to produce integrable systems with more dynamical variables. Recently, we observed such an effort to obtain systems of Sawada-Kotera (SK) and Kaup-Kuperschmidt (KK) equations [1, 2] by the use of Lax representations. The purpose of this paper is to show that the systems obtained in [1, 2] are easily obtained by a method that we call ${{ \mathcal M }}_{2}$-extensions of the SK and KK equations. This method is so general that it can be used for any integrable scalar equation.
Let ${{ \mathcal M }}_{2}$ be a special subclass of 2 × 2 matrices. Let $A\in {{ \mathcal M }}_{2}$ and be given by A = a1 I + a2 Σ where a1 and a2 are independent components of the matrix A, I is the 2 × 2 identity matrix, and1.3 ) for U. In componentwise the above equations give a system of equations for the dynamical variables u and v
$\begin{eqnarray}{\rm{\Sigma }}=\left(\begin{array}{ll}0 & \sigma \\ 1 & 0\end{array}\right),\end{eqnarray}$
where σ is a real constant. Since Σ2 = σ I, products of all such matrices are also in this subclass of matrices. Hence ${{ \mathcal M }}_{2}$ is a commutative subclass of 2 × 2 matrices. Due to the special properties of this subclass ${{ \mathcal M }}_{2}$ of 2 × 2 matrices we can generate new systems of integrable equations from scalar integrable equations. We call this method the ${{ \mathcal M }}_{2}$-extension of integrable scalar equations. As an illustration consider the well-known Korteweg–de Vries (KdV) equation ut = uxxx + 6uux with Lax pair L = D2 + u, ${ \mathcal A }=4{D}^{3}+6{uD}+3{u}_{x}$ so that the Lax equation is satisfied by virtue of the KdV equation $\begin{eqnarray}{L}_{t}+[L,{ \mathcal A }]=0,\end{eqnarray}$
and the recursion operator ${{ \mathcal R }}_{{KdV}}={D}^{2}+4u+2{u}_{x}{D}^{-1}$ [3]. Here D is the total x-derivative and D−1 = ∫x is the standard anti-derivative. Then ${{ \mathcal M }}_{2}$-extension of the KdV equation, its Lax pair, and recursion operator are, respectively, given as $\begin{eqnarray}{U}_{t}={U}_{{xxx}}+6{{UU}}_{x},\end{eqnarray}$
$\begin{eqnarray}L={{ID}}^{2}+U,\end{eqnarray}$
$\begin{eqnarray}{ \mathcal A }=4{{ID}}^{3}+6{UD}+3{U}_{x},\end{eqnarray}$
$\begin{eqnarray}{ \mathcal R }={{ID}}^{2}+4U+2{U}_{x}\,{D}^{-1},\end{eqnarray}$
where $\begin{eqnarray}U={uI}+v{\rm{\Sigma }}=\left(\begin{array}{ll}u & \sigma v\\ v & u\end{array}\right).\end{eqnarray}$
The pair L and ${ \mathcal A }$ solves the Lax equation due to the ${{ \mathcal M }}_{2}$-extension of the KdV equation ( $\begin{eqnarray}{u}_{t}={u}_{{xxx}}+6({{uu}}_{x}+\sigma {{vv}}_{x}),\end{eqnarray}$
$\begin{eqnarray}{v}_{t}={v}_{{xxx}}+6{\left({uv}\right)}_{x},\end{eqnarray}$
admitting the recursion operator $\begin{eqnarray}{ \mathcal R }=\left(\begin{array}{ll}{R}_{{\rm{KdV}}} & \,\sigma (4v+2{v}_{x}\,{D}^{-1})\\ 4v+2{v}_{x}\,{D}^{-1} & {R}_{{\rm{KdV}}}\end{array}\right).\end{eqnarray}$
It is interesting that the above extension of the KdV equation is equivalent to the pseudo-complexification of the KdV equation. First let σ = ε∣σ∣ where ε = 0, ± 1. Then scale $v\to \tfrac{v}{\sqrt{| \sigma | }}$ (for σ ≠ 0) so the above system becomes $\begin{eqnarray}{u}_{t}={u}_{{xxx}}+6({{uu}}_{x}+\epsilon {{vv}}_{x}),\end{eqnarray}$
$\begin{eqnarray}{v}_{t}={v}_{{xxx}}+6{\left({uv}\right)}_{x}.\end{eqnarray}$
For $\epsilon =0$ the above system is the extension of the KdV with its linearized equation for $v=\delta u$ (see [4]). For $\epsilon \ne 0$ this system is a consequence of the pseudo-complexification $u\to U=u+{ev}$ of the KdV equation where e is the pseudo-complex unit ${e}^{2}=\epsilon $. For complex numbers $\epsilon =-1$ but for pseudo-complex numbers $\epsilon =1$. Complex conjugation for both cases is the same ${e}^{* }=-e$. Hence our conclusion is that the ${{ \mathcal M }}_{2}$-extension of the KdV equation is the unification of linearization, complexification, and pseudo-complexification of the KdV equation. Our second conclusion is that this is valid in general.
We note that it is possible to define a second ${{ \mathcal M }}_{2}$-algebra by using a different unit Σ such that Σ2 = σ Σ, where σ is any real number. In this way we follow our approach to the KdV equation, for instance, we obtain different integrable coupled equations. Let u → U = uI + vΣ then we obtain the following integrable coupled equations [5, 6]1.4 )–(1.6 ). We shall consider these two ${{ \mathcal M }}_{2}$-algebras in more detail in a forthcoming work [7]. In the rest of this work we use only the first ${{ \mathcal M }}_{2}$-algebra.
$\begin{eqnarray}{u}_{t}={u}_{{xxx}}+6{{uu}}_{x},\end{eqnarray}$
$\begin{eqnarray}{v}_{t}={v}_{{xxx}}+6{\left({uv}\right)}_{x}+6\sigma \,{{vv}}_{x}.\end{eqnarray}$
An example of such unit is given as ${\rm{\Sigma }}=\left(\begin{array}{cc}0 & 0\\ 1 & \sigma \end{array}\right).$ One can obtain the Lax pair and the recursion operator of the above system by letting U = uI + vΣ in (We use the ${{ \mathcal M }}_{2}$-extension method on integrable scalar equations to obtain systems of integrable equations and new integrable nonlocal equations. This method consists of three main steps. The first step is to replace the dynamical variable of the integrable scalar equation by uI + vΣ where u and v are the dynamical variables of the system. Here, since Σ2 = σI the system of equations contains also the constant σ. We write the dynamical equations for u and v. By using the recursion operator of the scalar equation we obtain the recursion operator of the system for u and v. Furthermore, if the Hirota bilinear form of the scalar equation is known then we obtain the bilinear form of the system of equations. At this step we obtain an integrable system for u and v. The second step is to obtain the symmetrical version of the system by defining new dynamical variables q = u + v and r = u − v. At the same time one can obtain the recursion operator with respect to the dynamical variables q and r. The third step is to apply consistent reductions; standard (unshifted) nonlocal reductions r(x, t) = q(ε1x, ε2t) and $r(x,t)=\bar{q}({\epsilon }_{1}x,{\epsilon }_{2}t)$, and shifted nonlocal reductions r(x, t) = q(ε1x + x0, ε2t + t0) and $r(x,t)=\bar{q}({\epsilon }_{1}x+{x}_{0},{\epsilon }_{2}t+{t}_{0})$ for ${x}_{0},{t}_{0}\in {\mathbb{R}}$ where ${\epsilon }_{1}^{2}={\epsilon }_{2}^{2}=1$ to obtain standard nonlocal and shifted nonlocal reductions of the system for q and r [8–20]. All these equations are new and integrable. Using the reduction formulas, we can obtain the recursion operators of the nonlocal differential equations. Soliton solutions of the standard nonlocal and shifted nonlocal equations can be easily obtained by using soliton solutions of the systems and reduction formulas.
In 2 × 2 matrix algebra we have two subalgebras effective in our approach. It is possible to study the extension of the scalar integrable equations by using subalgebras of higher dimensional matrix algebras. We shall consider such extensions in later communications.
In the following section, we find ${{ \mathcal M }}_{2}$-extensions of the SK and KK equations, their recursion operators, and symmetrical versions of these systems. In section 3 we obtain nonlocal reductions of the SK and KK systems. In section 4 we find shifted nonlocal reductions of SK and KK systems. In section 5 we present Hirota bilinearization of SK and KK systems and give one-soliton solutions of these systems.
2. SK and KK systems
(1) SK equation, Lax pair and recursion operator
$\begin{eqnarray}{u}_{t}+{u}_{5x}+5{{uu}}_{{xxx}}+5{u}_{x}{u}_{{xx}}+5{u}^{2}{u}_{x}=0,\end{eqnarray}$
$\begin{eqnarray}L={D}^{3}+{uD},\end{eqnarray}$
$\begin{eqnarray}{ \mathcal A }=9{D}^{5}+15{{uD}}^{3}+15{u}_{x}{D}^{2}+5({u}^{2}+2{u}_{{xx}})D,\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{{ \mathcal R }}_{{SK}}={D}^{6}+6{{uD}}^{4}+9{u}_{x}{D}^{3}\\ +\,(9{u}^{2}+11{u}_{{xx}}){D}^{2}+(10{u}_{{xxx}}+21{{uu}}_{x})D\\ +\,4{u}^{3}+16{{uu}}_{{xx}}+6{u}_{x}^{2}+5{u}_{4x}\\ +\,{u}_{x}{D}^{-1}(2{u}_{{xx}}+{u}^{2})-{u}_{t}\,{D}^{-1}.\end{array}\end{eqnarray}$
(2) KK equation, Lax pair and recursion operator
$\begin{eqnarray}{u}_{t}+{u}_{5x}+10{{uu}}_{{xxx}}+25{u}_{x}{u}_{{xx}}+20{u}^{2}{u}_{x}=0,\end{eqnarray}$
$\begin{eqnarray}L={D}^{3}+2{uD}+{u}_{x},\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{ \mathcal A }=9{D}^{5}+3{{uD}}^{3}+45{u}_{x}{D}^{2}\\ +\,(20{u}^{2}+35{u}_{{xx}})D+10({u}^{2}+{u}_{{xx}}),\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{{ \mathcal R }}_{{KK}}={D}^{6}+12{{uD}}^{4}+36{u}_{x}{D}^{3}\\ +\,(36{u}^{2}+49{u}_{{xx}}){D}^{2}+(35{u}_{{xxx}}+120{{uu}}_{x})D\\ +\,32{u}^{3}+82{{uu}}_{{xx}}+69{u}_{x}^{2}+13{u}_{4x}\\ +\,2{u}_{x}{D}^{-1}({u}_{{xx}}+4{u}^{2})-2{u}_{t}\,{D}^{-1}.\end{array}\end{eqnarray}$
${{ \mathcal M }}_{2}$-extensions of these equations, Lax pairs and recursion operators are, respectively, given as(3) SK system, Lax pair and recursion operator2.13 ) and (2.14 ) as
$\begin{eqnarray}{U}_{t}+{U}_{5x}+5{{UU}}_{{xxx}}+5{U}_{x}{U}_{{xx}}+5{U}^{2}{U}_{x}=0,\end{eqnarray}$
$\begin{eqnarray}L={{ID}}^{3}+{UD},\end{eqnarray}$
$\begin{eqnarray}{ \mathcal A }=9{{ID}}^{5}+15{{UD}}^{3}+15{U}_{x}{D}^{2}+5({U}^{2}+2{U}_{{xx}})D,\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{ \mathcal R }={{ID}}^{6}+6{{UD}}^{4}+9{U}_{x}{D}^{3}\\ +\,(9{U}^{2}+11{U}_{{xx}}){D}^{2}+(10{U}_{{xxx}}+21{{UU}}_{x})D\\ +\,4{U}^{3}+16{{UU}}_{{xx}}+6{U}_{x}^{2}+5{U}_{4x}\\ +\,{U}_{x}{D}^{-1}(2{U}_{{xx}}+{U}^{2})-{U}_{t}\,{D}^{-1}.\end{array}\end{eqnarray}$
The above equations correspond to the system of equations for the dynamical variables u and v as $\begin{eqnarray}\begin{array}{l}{u}_{t}+{u}_{5x}+5{{uu}}_{{xxx}}+5{u}_{x}{u}_{{xx}}\\ +\,5{u}^{2}{u}_{x}+5\sigma {\left({{vv}}_{{xx}}+{v}^{2}u\right)}_{x}=0,\end{array}\end{eqnarray}$
$\begin{eqnarray}{v}_{t}+{v}_{5x}+5{\left({{vu}}_{{xx}}+{{uv}}_{{xx}}+{u}^{2}v\right)}_{x}+5\sigma {v}^{2}{v}_{x}=0.\end{eqnarray}$
The recursion operator of this system is $\begin{eqnarray}{ \mathcal R }=\left(\begin{array}{ll}{R}_{{SK}}+\sigma \,{A}_{11} & \quad \sigma {A}_{21}\\ {A}_{21} & {R}_{{SK}}+\sigma \,{A}_{11}\end{array}\right),\end{eqnarray}$
where $\begin{eqnarray}\begin{array}{l}{A}_{11}=9{v}^{2}{D}^{2}+21{{vv}}_{x}D+12{{uv}}^{2}+16{{vv}}_{{xx}}\\ +\,6{v}_{x}^{2}+{u}_{x}{D}^{-1}{v}^{2}+2{v}_{x}{D}^{-1}({v}_{{xx}}+{uv}),\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{A}_{21}=-{v}_{t}+6{{vD}}^{4}+9{v}_{x}{D}^{3}+(18{uv}+11{v}_{{xx}}){D}^{2}\\ +\,(10{v}_{{xxx}}+21{\left({uv}\right)}_{x})D+4(\sigma {v}^{3}+3{u}^{2}v)\\ +\,16({{vu}}_{{xx}}+{{uv}}_{{xx}})+12{u}_{x}{v}_{x}+5{v}_{4x}\\ +\,{v}_{x}{D}^{-1}(2{u}_{{xx}}+{u}^{2}+\sigma {v}^{2})+2{u}_{x}{D}^{-1}({v}_{{xx}}+{uv}).\end{array}\end{eqnarray}$
By letting u = q + r, v = q − r, and t → at, where a is a constant, we get symmetrical version of the system ( $\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{5}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){r}_{{xx}}]{q}_{x}+10[(\sigma +1){q}^{2}\\ -\,(\sigma -1){qr}]{q}_{x}+5(\sigma -1)({r}^{2}-{q}^{2}){r}_{x}\\ +\,\displaystyle \frac{5}{2}(\sigma -1)({r}_{{xx}}-{q}_{{xx}}){r}_{x}+\displaystyle \frac{5}{2}[(\sigma +3)q-(\sigma -1)r]{q}_{{xxx}}\\ +\displaystyle \frac{5}{2}(\sigma -1)(r-q){r}_{{xxx}}=0,\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{{ar}}_{t}+{r}_{5x}+\displaystyle \frac{5}{2}[(\sigma +3){r}_{{xx}}-(\sigma -1){q}_{{xx}}]{r}_{x}+10[(\sigma +1){r}^{2}\\ -\,(\sigma -1){qr}]{r}_{x}+5(\sigma -1)({q}^{2}-{r}^{2}){q}_{x}\\ +\,\displaystyle \frac{5}{2}(\sigma -1)({q}_{{xx}}-{r}_{{xx}}){q}_{x}+\displaystyle \frac{5}{2}[(\sigma +3)r-(\sigma -1)q]{r}_{{xxx}}\\ +\,\displaystyle \frac{5}{2}(\sigma -1)(q-r){q}_{{xxx}}=0.\end{array}\end{eqnarray}$
(4) KK system, Lax pair and recursion operator2.24 ) and (2.25 ) as
$\begin{eqnarray}{U}_{t}+{U}_{5x}+10{{UU}}_{{xxx}}+25{U}_{x}{U}_{{xx}}+20{U}^{2}{U}_{x}=0,\end{eqnarray}$
$\begin{eqnarray}L={{ID}}^{3}+2{UD}+{U}_{x},\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{ \mathcal A } & = & 9{{ID}}^{5}+3{{UD}}^{3}+45{U}_{x}{D}^{2}+(20{U}^{2}+35{U}_{{xx}})D\\ & & +10({U}^{2}+{U}_{{xx}}),\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{ \mathcal R }={{ID}}^{6}+12{{UD}}^{4}+36{U}_{x}{D}^{3}+(36{U}^{2}+49{U}_{{xx}}){D}^{2}\\ \,+\,(35{U}_{{xxx}}+120{{UU}}_{x})D\\ \,+\,32{U}^{3}+82{{UU}}_{{xx}}+69{U}_{x}^{2}+13{U}_{4x}\\ \,+\,2{U}_{x}{D}^{-1}({U}_{{xx}}+4{U}^{2})-2{U}_{t}\,{D}^{-1}.\end{array}\end{eqnarray}$
In componentwise the above equations give the following system of equations for the dynamical variables u and v $\begin{eqnarray}\begin{array}{l}{u}_{t}+{u}_{5x}+10{{uu}}_{{xxx}}+25{u}_{x}{u}_{{xx}}+20{u}^{2}{u}_{x}\\ \,+\,5\sigma (2{{vv}}_{{xxx}}+5{v}_{x}{v}_{{xx}}+4{\left({v}^{2}u\right)}_{x})=0,\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{v}_{t}+{v}_{5x}+5(2{{vu}}_{{xxx}}+5{v}_{x}{u}_{{xx}}+2{{uv}}_{{xxx}}\\ \,+\,5{u}_{x}{v}_{{xx}}+4{\left({u}^{2}v\right)}_{x})+20\sigma {v}^{2}{v}_{x}=0.\end{array}\end{eqnarray}$
The recursion operator of the above system is $\begin{eqnarray}{ \mathcal R }=\left(\begin{array}{ll}{R}_{{KK}}+\sigma \,{A}_{11} & \sigma {A}_{21}\\ {A}_{21} & {R}_{{KK}}+\sigma \,{A}_{11}\end{array}\right),\end{eqnarray}$
where $\begin{eqnarray}\begin{array}{l}{A}_{11}=36{v}^{2}{D}^{2}+120{{vv}}_{x}D+96{{uv}}^{2}+82{{vv}}_{{xx}}\\ +\,69{v}_{x}^{2}+8{u}_{x}{D}^{-1}{v}^{2}+2{v}_{x}{D}^{-1}({v}_{{xx}}+8{uv}),\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{A}_{21}=-2{v}_{t}+12{{vD}}^{4}+36{v}_{x}{D}^{3}+(72{uv}+49{v}_{{xx}}){D}^{2}\\ +(35{v}_{{xxx}}+120{\left({uv}\right)}_{x})D\\ +\,32(\sigma {v}^{3}+3{u}^{2}v)+82({{vu}}_{{xx}}+{{uv}}_{{xx}})+138{u}_{x}{v}_{x}\\ +\,13{v}_{4x}+2{v}_{x}{D}^{-1}({u}_{{xx}}+4{u}^{2}+\sigma 4{v}^{2})\\ +2{u}_{x}{D}^{-1}({v}_{{xx}}+8{uv}).\end{array}\end{eqnarray}$
Letting u = q + r, v = q − r, and t → at, where a is a constant, yields symmetrical version of the system ( $\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{25}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){r}_{{xx}}]{q}_{x}\\ +\,40[(\sigma +1){q}^{2}-(\sigma -1){qr}]{q}_{x}\\ +20(\sigma -1)({r}^{2}-{q}^{2}){r}_{x}\\ +\,\displaystyle \frac{25}{2}(\sigma -1)({r}_{{xx}}-{q}_{{xx}}){r}_{x}\\ +5[(\sigma +3)q-(\sigma -1)r]{q}_{{xxx}}\\ +\,5(\sigma -1)(r-q){r}_{{xxx}}=0,\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}{{ar}}_{t}+{r}_{5x}+\displaystyle \frac{25}{2}[(\sigma +3){r}_{{xx}}-(\sigma -1){q}_{{xx}}]{r}_{x}\\ +\,40[(\sigma +1){r}^{2}-(\sigma -1){qr}]{r}_{x}\\ +20(\sigma -1)({q}^{2}-{r}^{2}){q}_{x}\\ +\,\displaystyle \frac{25}{2}(\sigma -1)({q}_{{xx}}-{r}_{{xx}}){q}_{x}\\ +\,5[(\sigma +3)r-(\sigma -1)q]{r}_{{xxx}}\\ +\,5(\sigma -1)(q-r){q}_{{xxx}}=0.\end{array}\end{eqnarray}$
We use the symmetrical versions of systems to obtain nonlocal reductions of them which will be the subject of the next section.
3. Nonlocal reductions
In the last decade, there has been intensive interest in obtaining new integrable nonlocal equations and studying the properties of these equations [8–14]. Here we give some new nonlocal equations of fifth order, namely nonlocal SK and nonlocal KK equations. The above symmetrical versions of SK (2.18 ), (2.19 ), and KK (2.29 ), (2.30 ) systems are good candidates to obtain new nonlocal integrable equations of fifth order.
(1) Nonlocal SK equations:
Consider the symmetrical SK system (2.18 ) and (2.19 ).
(a) r(x, t) = q(ϵ1x, ϵ2t), ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$.
When we apply this real nonlocal reduction on the SK system (2.18 ) and (2.19 ) we get the condition ϵ1ϵ2 = 1 for consistency. Therefore here we have only one nonlocal reduction r = q(–x, –t) which reduces the system (2.18 ), (2.19 ) to the following nonlocal space-time reversal SK equation3.1 ), particularly for σ = 0 and σ = –1, to find soliton and periodic wave solutions of this equation with the help of the Jacobi elliptic function expansion method and Hirota method. They did not consider other types of nonlocalities of the SK equation.
$\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{5}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){q}_{{xx}}^{\varepsilon }]{q}_{x}\\ +\,10[(\sigma +1){q}^{2}-(\sigma -1){{qq}}^{\varepsilon }]{q}_{x}\\ +\,5(\sigma -1)\left({\left({q}^{\varepsilon }\right)}^{2}-{q}^{2}\right){q}_{x}^{\varepsilon }+\displaystyle \frac{5}{2}(\sigma -1)({q}_{{xx}}^{\varepsilon }-{q}_{{xx}}){q}_{x}^{\varepsilon }\\ +\,\displaystyle \frac{5}{2}[(\sigma +3)q-(\sigma -1){q}^{\varepsilon }]{q}_{{xxx}}+\,\displaystyle \frac{5}{2}(\sigma -1)({q}^{\varepsilon }-q){q}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where qϵ = q(–x, –t). In [2], Qi-Liang et al obtained the same nonlocal SK equation from the local SK equation by using a discrete symmetry group without giving a symmetrical local SK system. They analyzed ((b) $r(x,t)=\bar{q}({\varepsilon }_{1}x,{\varepsilon }_{2}t)$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$.
Applying the complex nonlocal reduction $r(x,t)=\bar{q}({\varepsilon }_{1}x,{\varepsilon }_{2}t)$ to the symmetrical SK system (2.18 ) and (2.19 ) yields the constraint2.18 ), (2.19 ) reduces to nonlocal space reversal SK equation for (ϵ1, ϵ2) = (–1, 1) with $a=-\bar{a};$ nonlocal time reversal SK equation for (ϵ1, ϵ2) = (1, –1) with $a=-\bar{a};$ nonlocal space-time reversal equation SK for (ϵ1, ϵ2) = (–1, –1) with $a=\bar{a}$ given by
$\begin{eqnarray}\bar{a}{\varepsilon }_{1}{\varepsilon }_{2}=a\end{eqnarray}$
for consistency. The system ( $\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{5}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){\bar{q}}_{{xx}}^{\varepsilon }]{q}_{x}\\ +10[(\sigma +1){q}^{2}-(\sigma -1)q{\bar{q}}^{\varepsilon }]{q}_{x}\\ +\,5(\sigma -1)\left({\left({\bar{q}}^{\varepsilon }\right)}^{2}-{q}^{2}\right){\bar{q}}_{x}^{\varepsilon }\\ +\,\displaystyle \frac{5}{2}(\sigma -1)({\bar{q}}_{{xx}}^{\varepsilon }-{q}_{{xx}}){\bar{q}}_{x}^{\varepsilon }\\ +\,\displaystyle \frac{5}{2}[(\sigma +3)q-(\sigma -1){\bar{q}}^{\varepsilon }]{q}_{{xxx}}\\ +\,\displaystyle \frac{5}{2}(\sigma -1)({\bar{q}}^{\varepsilon }-q){\bar{q}}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where ${\bar{q}}^{\varepsilon }=\bar{q}({\varepsilon }_{1}x,{\varepsilon }_{2}t)$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$. Hence the above equation consists of three different reductions representing different nonlocal complex SK equations.(2) Nonlocal KK equations:
Consider the symmetrical KK system (2.24 ) and (2.25 ).
(a) r(x, t) = q(ϵ1x, ϵ2t), ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$.
Similar to the symmetrical SK system, applying the reduction r(x, t) = q(ϵ1x, ϵ2t) to the symmetrical KK system (2.24 ) and (2.25 ) gives the constraint ϵ1ϵ2 = 1 for consistency. Hence we have only one real nonlocal reduction r = q( − x, − t) which reduces the system (2.29 ) and (2.30 ) to the nonlocal space-time reversal KK equation3.4 ) by using a special traveling wave ansatz consisting of Jacobi elliptic functions. They did not analyze other types of nonlocalities of the KK equation.
$\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{25}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){q}_{{xx}}^{\varepsilon }]{q}_{x}\\ +40[(\sigma +1){q}^{2}-(\sigma -1){{qq}}^{\varepsilon }]{q}_{x}\\ +20(\sigma -1)\left({\left({q}^{\varepsilon }\right)}^{2}-{q}^{2}\right){q}_{x}^{\varepsilon }+\displaystyle \frac{25}{2}(\sigma -1)({q}_{{xx}}^{\varepsilon }-{q}_{{xx}}){q}_{x}^{\varepsilon }\\ +5[(\sigma +3)q-(\sigma -1){q}^{\varepsilon }]{q}_{{xxx}}+5(\sigma -1)({q}^{\varepsilon }-q){q}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where qϵ = q(–x, –t). In [1], Qi-Liang et al extended the generalized local fifth-order equation to the same nonlocal KK equation for σ = − 1 without deriving a symmetrical local KK system. They obtained periodic wave solutions of the equation ((b) $r(x,t)=\bar{q}({\varepsilon }_{1}x,{\varepsilon }_{2}t)$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$.
When we apply this complex nonlocal reduction to the symmetrical KK system (2.29 ) and (2.30 ) we obtain the condition $\bar{a}{\varepsilon }_{1}{\varepsilon }_{2}=a$ for consistency as in the SK system case. The KK system (2.29 ), (2.30 ) reduces to nonlocal space reversal KK equation for (ϵ1, ϵ2) = (–1, 1) with $a=\mbox{--}\bar{a};$ nonlocal time reversal KK equation for (ϵ1, ϵ2) = (1, –1) with $a=\mbox{--}\bar{a};$ nonlocal space-time reversal KK equation for (ϵ1, ϵ2) = (–1, –1) with $a=\bar{a}$. Explicitly, we have
$\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{25}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){\bar{q}}_{{xx}}^{\varepsilon }]{q}_{x}\\ +\,40[(\sigma +1){q}^{2}-(\sigma -1)q{\bar{q}}^{\varepsilon }]{q}_{x}\\ +\,20(\sigma -1)\left({\left({\bar{q}}^{\varepsilon }\right)}^{2}-{q}^{2}\right){\bar{q}}_{x}^{\varepsilon }+\displaystyle \frac{25}{2}(\sigma -1)({\bar{q}}_{{xx}}^{\varepsilon }-{q}_{{xx}}){\bar{q}}_{x}^{\varepsilon }\\ +\,5[(\sigma +3)q-(\sigma -1){\bar{q}}^{\varepsilon }]{q}_{{xxx}}+\,5(\sigma -1)({\bar{q}}^{\varepsilon }-q){\bar{q}}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where ${\bar{q}}^{\varepsilon }=\bar{q}({\varepsilon }_{1}x,{\varepsilon }_{2}t)$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$. Then the above equation consists of three different reductions representing different nonlocal complex KK equations.By using the reduction formulas (1).a, (1).b, (2).a, and (2).b, and the recursion operators of SK and KK systems, i.e., (
4. Shifted nonlocal reductions
After quite a few works on integrable nonlocal reductions, Ablowitz and Musslimani generalized standard nonlocal reductions to shifted nonlocal reductions in [15] as
$\begin{eqnarray}\begin{array}{l}r=q({\varepsilon }_{1}x+{x}_{0},{\varepsilon }_{2}t+{t}_{0}),\,\,\,r=\bar{q}({\varepsilon }_{1}x+{x}_{0},{\varepsilon }_{2}t+{t}_{0}),\\ {x}_{0},{t}_{0}\in {\mathbb{R}},\end{array}\end{eqnarray}$
for ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$ and (ϵ1, ϵ2) ≠ (1, 1). It is obvious that if x0 = t0 = 0, the shifted reductions become standard (unshifted) nonlocal reductions. There are also several works on integrable shifted nonlocal equations and their different type of solutions obtained by various types of methods [16–20].Here we give shifted nonlocal SK and KK equations by applying the above shifted nonlocal reductions to the symmetrical SK system (2.18 ), (2.19 ), and the symmetrical KK system (2.29 ), (2.30 ).
(1) Shifted nonlocal SK equations:
(a) r(x, t) = q(ϵ1x + x0, ϵ2t + t0), ${x}_{0},{t}_{0}\in {\mathbb{R}}$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$.
Using this real shifted nonlocal reduction on the SK system (2.18 ), (2.19 ) requires the condition ϵ1ϵ2 = 1 to be satisfied for consistency. Hence we have only one shifted nonlocal reduction r = q(–x + x0, –t + t0) and the corresponding shifted nonlocal space-time reversal SK equation is
$\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{5}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){q}_{{xx}}^{\varepsilon }]{q}_{x}\\ +\,10[(\sigma +1){q}^{2}-(\sigma -1){{qq}}^{\varepsilon }]{q}_{x}\\ +\,5(\sigma -1)\left({\left({q}^{\varepsilon }\right)}^{2}-{q}^{2}\right){q}_{x}^{\varepsilon }\\ +\,\displaystyle \frac{5}{2}(\sigma -1)({q}_{{xx}}^{\varepsilon }-{q}_{{xx}}){q}_{x}^{\varepsilon }\\ +\,\displaystyle \frac{5}{2}[(\sigma +3)q-(\sigma -1){q}^{\varepsilon }]{q}_{{xxx}}\\ +\,\displaystyle \frac{5}{2}(\sigma -1)({q}^{\varepsilon }-q){q}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where qϵ = q(–x + x0, − t + t0), ${x}_{0},{t}_{0}\in {\mathbb{R}}$.(b) $r(x,t)=\bar{q}({\varepsilon }_{1}x+{x}_{0},{\varepsilon }_{2}t+{t}_{0})$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$.
Applying the complex shifted nonlocal reduction to the system (2.18 ), (2.19 ) gives the following constraint
$\begin{eqnarray}\bar{a}{\varepsilon }_{1}{\varepsilon }_{2}=a\end{eqnarray}$
for consistency. Therefore the symmetrical SK system reduces to shifted nonlocal SK equations represented by $\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{5}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){\bar{q}}_{{xx}}^{\varepsilon }]{q}_{x}\\ +\,10[(\sigma +1){q}^{2}-(\sigma -1)q{\bar{q}}^{\varepsilon }]{q}_{x}\\ +\,5(\sigma -1)\left({\left({\bar{q}}^{\varepsilon }\right)}^{2}-{q}^{2}\right){\bar{q}}_{x}^{\varepsilon }+\displaystyle \frac{5}{2}(\sigma -1)({\bar{q}}_{{xx}}^{\varepsilon }-{q}_{{xx}}){\bar{q}}_{x}^{\varepsilon }\\ +\,\displaystyle \frac{5}{2}[(\sigma +3)q-(\sigma -1){\bar{q}}^{\varepsilon }]{q}_{{xxx}}\\ +\,\displaystyle \frac{5}{2}(\sigma -1)({\bar{q}}^{\varepsilon }-q){\bar{q}}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where ${\bar{q}}^{\varepsilon }=\bar{q}({\varepsilon }_{1}x+{x}_{0},{\varepsilon }_{2}t+{t}_{0})$, ${x}_{0},{t}_{0}\in {\mathbb{R}}$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$. The above equation consists three shifted nonlocal SK equations; shifted nonlocal space reversal SK equation for (ϵ1, ϵ2) = (–1, 1), t0 = 0, $a=-\bar{a}$, shifted nonlocal time reversal SK equation for (ϵ1, ϵ2) = (1, –1), x0 = 0, $a=\mbox{--}\bar{a}$, and shifted nonlocal space-time reversal equation SK equation for (ϵ1, ϵ2) = (–1, –1), $a=\bar{a}$.(2) Shifted nonlocal KK equations:
(a) r(x, t) = q(ϵ1x + x0, ϵ2t + t0), ${x}_{0},{t}_{0}\in {\mathbb{R}}$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$.
Applying the reduction r(x, t) = q(ϵ1x + x0, ϵ2t + t0) to the system (2.24 ) and (2.25 ) yields the condition ϵ1ϵ2 = 1 for consistency. Similar to the SK system case, we have only one real shifted nonlocal reduction r = q(–x + x0, − t + t0) reducing the KK system (2.29 ) and (2.30 ) to the shifted nonlocal space-time reversal KK equation
$\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{25}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){q}_{{xx}}^{\varepsilon }]{q}_{x}\\ +40[(\sigma +1){q}^{2}-(\sigma -1){{qq}}^{\varepsilon }]{q}_{x}\\ +\,20(\sigma -1)\left({\left({q}^{\varepsilon }\right)}^{2}-{q}^{2}\right){q}_{x}^{\varepsilon }\\ +\displaystyle \frac{25}{2}(\sigma -1)({q}_{{xx}}^{\varepsilon }-{q}_{{xx}}){q}_{x}^{\varepsilon }\\ +\,5[(\sigma +3)q-(\sigma -1){q}^{\varepsilon }]{q}_{{xxx}}\\ +\,5(\sigma -1)({q}^{\varepsilon }-q){q}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where qϵ = q( − x + x0, − t + t0), ${x}_{0},{t}_{0}\in {\mathbb{R}}$.(b) $r(x,t)=\bar{q}({\varepsilon }_{1}x+{x}_{0},{\varepsilon }_{2}t+{t}_{0})$, ${x}_{0},{t}_{0}\in {\mathbb{R}}$, ${\varepsilon }_{1}^{2}\,={\varepsilon }_{2}^{2}=1$.
Under the complex shifted nonlocal reduction we get the condition $\bar{a}{\varepsilon }_{1}{\varepsilon }_{2}=a$ for consistency and the symmetrical KK system (2.29 ), (2.30 ) reduces to three different shifted nonlocal KK equations given by
$\begin{eqnarray}\begin{array}{l}{{aq}}_{t}+{q}_{5x}+\displaystyle \frac{25}{2}[(\sigma +3){q}_{{xx}}-(\sigma -1){\bar{q}}_{{xx}}^{\varepsilon }]{q}_{x}\\ +\,40[(\sigma +1){q}^{2}-(\sigma -1)q{\bar{q}}^{\varepsilon }]{q}_{x}\\ +\,20(\sigma -1)\left({\left({\bar{q}}^{\varepsilon }\right)}^{2}-{q}^{2}\right){\bar{q}}_{x}^{\varepsilon }+\displaystyle \frac{25}{2}(\sigma -1)({\bar{q}}_{{xx}}^{\varepsilon }-{q}_{{xx}}){\bar{q}}_{x}^{\varepsilon }\\ +\,5[(\sigma +3)q-(\sigma -1){\bar{q}}^{\varepsilon }]{q}_{{xxx}}+\,5(\sigma -1)({\bar{q}}^{\varepsilon }-q){\bar{q}}_{{xxx}}^{\varepsilon }=0,\end{array}\end{eqnarray}$
where ${\bar{q}}^{\varepsilon }=\bar{q}({\varepsilon }_{1}x+{x}_{0},{\varepsilon }_{2}t+{t}_{0})$, ${x}_{0},{t}_{0}\in {\mathbb{R}}$, ${\varepsilon }_{1}^{2}={\varepsilon }_{2}^{2}=1$. Indeed we have shifted nonlocal space reversal KK equation for (ϵ1, ϵ2) = (–1, 1), t0 = 0, $a=-\bar{a}$, shifted nonlocal time reversal KK equation for (ϵ1, ϵ2) = (1, –1), x0 = 0, $a=\mbox{--}\bar{a}$, and shifted nonlocal space-time reversal KK equation for (ϵ1, ϵ2) = (–1, –1), $a=\bar{a}$.5. Hirota bilinearization and one-soliton solution
It is also possible to write the Hirota bilinear forms of the extended equations. Starting with the Hirota bilinear forms of the scalar SK and KK equations and writing them for extended variable U we obtain the corresponding Hirota forms of SK and KK systems.
(i) For the SK system (2.13 ) and (2.14 ).
Let $u=6{\left(\mathrm{ln}(f)\right)}_{{xx}}$ then the Hirota bilinear form of SK equation is given as [28–30]2.13 ), (2.14 ), take ${f}_{1}={\alpha }_{1}+{\alpha }_{2}{{\rm{e}}}^{{k}_{1}x+{\omega }_{1}t+{\delta }_{1}}$ and ${f}_{2}={\alpha }_{3}+{\alpha }_{4}{{\rm{e}}}^{{k}_{2}x+{\omega }_{2}t+{\delta }_{2}}$ for some constants kj, ωj, δj, j = 1, 2 and αi, i = 1, 2, 3, 4. Inserting this choice into the Hirota bilinear form (5.4 ) and (5.5 ) yields
$\begin{eqnarray}{D}_{x}\left({D}_{t}+{D}_{x}^{5}\right)\{f\cdot f\}=0.\end{eqnarray}$
For the system of equations we make use of the above bilinearization. We let $U=6{\left({F}^{-1}\,{F}_{x}\right)}_{x}$ where F = f1I + f2Σ and ${F}^{-1}=\tfrac{1}{{f}_{1}^{2}-\sigma {f}_{2}^{2}}\,({f}_{1}I-{f}_{2}{\rm{\Sigma }})$. Here f1 and f2 are the functions to be determined by the Hirota method. We get $\begin{eqnarray}{{FF}}_{6x}-6{F}_{x}{F}_{5x}+15{F}_{{xx}}{F}_{4x}-10{F}_{{xxx}}^{2}+{{FF}}_{{xt}}-{F}_{x}{F}_{t}=0\end{eqnarray}$
or equivalently $\begin{eqnarray}{D}_{x}\left({D}_{t}+{D}_{x}^{5}\right)\{F\cdot F\}=0.\end{eqnarray}$
When we write the above equation in componentwise we obtain $\begin{eqnarray}{D}_{x}\left({D}_{t}+{D}_{x}^{5}\right)\{{f}_{1}\cdot {f}_{1}+\sigma {f}_{2}\cdot {f}_{2}\}=0,\end{eqnarray}$
$\begin{eqnarray}{D}_{x}\left({D}_{t}+{D}_{x}^{5}\right)\{{f}_{1}\cdot {f}_{2}\}=0.\end{eqnarray}$
Hence solving f1 and f2 from the above expressions and using them in $U=6{\left({F}^{-1}\,{F}_{x}\right)}_{x}={uI}+v{\rm{\Sigma }}$, we obtain u and v in terms of f1 and f2. To find one-soliton solution of the system ( $\begin{eqnarray}{k}_{2}={k}_{1},\quad {\omega }_{2}={\omega }_{1}=-{k}_{1}^{5},\end{eqnarray}$
and $\begin{eqnarray}u(x,t)=\displaystyle \frac{{U}_{1}(x,t)}{{U}_{2}(x,t)},\quad v(x,t)=\displaystyle \frac{{U}_{3}(x,t)}{{U}_{2}(x,t)},\end{eqnarray}$
where $\begin{eqnarray}\begin{array}{rcl}{U}_{1}(x,t) & = & 7-6{k}_{1}^{2}\left[(\sigma {\alpha }_{3}^{2}-{\alpha }_{1}^{2})({\alpha }_{1}{\alpha }_{2}{{\rm{e}}}^{{\delta }_{1}}-\sigma {\alpha }_{3}{\alpha }_{4}{{\rm{e}}}^{{\delta }_{2}}){{\rm{e}}}^{\phi }\right.\\ & & +2(\sigma {\alpha }_{3}^{2}-{\alpha }_{1}^{2})({\alpha }_{2}^{2}{{\rm{e}}}^{2{\delta }_{1}}-\sigma {\alpha }_{4}^{2}{{\rm{e}}}^{2{\delta }_{2}}){{\rm{e}}}^{2\phi }\\ & & \left.+({\alpha }_{1}{\alpha }_{2}{{\rm{e}}}^{{\delta }_{1}}-\sigma {\alpha }_{3}{\alpha }_{4}{{\rm{e}}}^{{\delta }_{2}})(\sigma {\alpha }_{4}^{2}{{\rm{e}}}^{2{\delta }_{2}}-{\alpha }_{2}^{2}{{\rm{e}}}^{2{\delta }_{1}}){{\rm{e}}}^{3\phi }\right],\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{U}_{2}(x,t) & = & \left[({\alpha }_{1}^{2}-\sigma {\alpha }_{3}^{2})+2({\alpha }_{1}{\alpha }_{2}{{\rm{e}}}^{{\delta }_{1}}-\sigma {\alpha }_{3}{\alpha }_{4}{{\rm{e}}}^{{\delta }_{2}}){{\rm{e}}}^{\phi }\right.\\ & & {\left.+({\alpha }_{2}^{2}{{\rm{e}}}^{2{\delta }_{1}}-\sigma {\alpha }_{4}^{2}{{\rm{e}}}^{2{\delta }_{2}}){{\rm{e}}}^{2\phi }\right]}^{2},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{U}_{3}(x,t) & = & 6{k}_{1}^{2}\left[(\sigma {\alpha }_{3}^{2}-{\alpha }_{1}^{2})({\alpha }_{2}{\alpha }_{3}{{\rm{e}}}^{{\delta }_{1}}-{\alpha }_{1}{\alpha }_{4}{{\rm{e}}}^{{\delta }_{2}}){{\rm{e}}}^{\phi }\right.\\ & & \left.+({\alpha }_{2}{\alpha }_{3}{{\rm{e}}}^{{\delta }_{1}}-{\alpha }_{1}{\alpha }_{4}{{\rm{e}}}^{{\delta }_{1}})({\alpha }_{2}^{2}{{\rm{e}}}^{2{\delta }_{1}}-\sigma {\alpha }_{4}^{2}{{\rm{e}}}^{2{\delta }_{2}}){{\rm{e}}}^{3\phi }\right],\end{array}\end{eqnarray}$
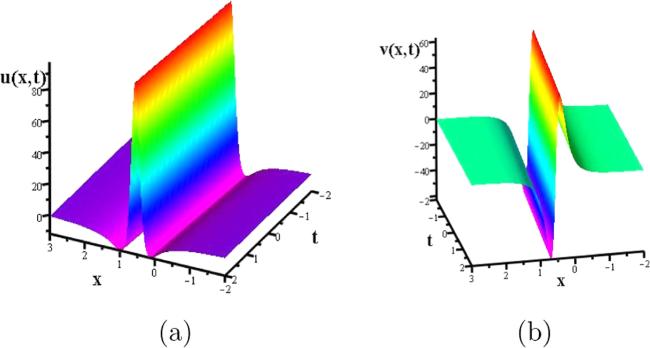
for $\phi ={k}_{1}x-{k}_{1}^{5}t$.Take particular values for the parameters of the solution (
$\begin{eqnarray}\begin{array}{l}u(x,t)=\displaystyle \frac{12{{\rm{e}}}^{\tfrac{1}{2}x-\tfrac{1}{32}t}[65{{\rm{e}}}^{\tfrac{1}{2}x-\tfrac{1}{32}t}-26{{\rm{e}}}^{x-\tfrac{1}{16}t}-40]}{{\left[32{{\rm{e}}}^{\tfrac{1}{2}x-\tfrac{1}{32}t}-13{{\rm{e}}}^{x-\tfrac{1}{16}t}-20\right]}^{2}},\\ v(x,t)=\displaystyle \frac{-3{{\rm{e}}}^{\tfrac{1}{2}x-\tfrac{1}{32}t}[13{{\rm{e}}}^{x-\tfrac{1}{16}t}-20]}{{\left[32{{\rm{e}}}^{\tfrac{1}{2}x-\tfrac{1}{32}t}-13{{\rm{e}}}^{x-\tfrac{1}{16}t}-20\right]}^{2}}.\end{array}\end{eqnarray}$
The graphs of the above solutions are given in figure 1.
Figure 1. One-soliton solution (u(x, t), v(x, t)) of the SK system ( |
(ii) For the KK system (2.24 ) and (2.25 ).
Letting $u=\tfrac{3}{2}{\left(\mathrm{ln}(f)\right)}_{{xx}}$ yields the Hirota bilinear form of KK equation as [28, 31, 32]2.24 ), (2.25 ) we take ${f}_{1}={\alpha }_{0}+{\alpha }_{1}{{\rm{e}}}^{{\theta }_{1}}+{\alpha }_{2}{{\rm{e}}}^{2{\theta }_{1}}$, ${f}_{2}={\alpha }_{3}+{\alpha }_{4}{{\rm{e}}}^{{\theta }_{1}}$, ${g}_{1}={\alpha }_{5}{{\rm{e}}}^{{\theta }_{1}}$, and ${g}_{2}={\alpha }_{6}{{\rm{e}}}^{{\theta }_{1}}$, where θ1 = k1x + ω1t + δ1 for some constants k1, ω1, δ1, and αj, j = 1,…,6. From the above system we get ${\omega }_{1}=-{k}_{1}^{5}$ and the following constraints:2.24 ), (2.25 ) is given by the pair (u,v)
$\begin{eqnarray}(16{D}_{x}{D}_{t}+{D}_{x}^{6})\{f\cdot f\}+20{D}_{x}^{2}\{f\cdot g\}=0,\end{eqnarray}$
$\begin{eqnarray}{D}_{x}^{4}\{f\cdot f\}-\displaystyle \frac{4}{3}{fg}=0,\end{eqnarray}$
where g is an auxiliary function. Similar to the SK system, we let $U=\tfrac{3}{2}{\left({F}^{-1}\,{F}_{x}\right)}_{x}$ where F = f1I + f2Σ. We determine f1 and f2 by the Hirota method. We get $\begin{eqnarray}\begin{array}{l}32({{FF}}_{{xt}}-{F}_{x}{F}_{t})+2({{FF}}_{6x}-6{F}_{x}{F}_{5x}+15{F}_{{xx}}{F}_{4x}-10{F}_{{xxx}}^{2})\\ +20({F}_{{xx}}G-2{F}_{x}{G}_{x}+{{FG}}_{{xx}})=0,\end{array}\end{eqnarray}$
$\begin{eqnarray}2({{FF}}_{4x}-4{F}_{x}{F}_{{xxx}}+6{F}_{{xx}}^{2})-\displaystyle \frac{4}{3}{FG}=0,\end{eqnarray}$
which is equivalent to $\begin{eqnarray}(16{D}_{x}{D}_{t}+{D}_{x}^{6})\{F\cdot F\}+20{D}_{x}^{2}\{F\cdot G\}=0,\end{eqnarray}$
$\begin{eqnarray}{D}_{x}^{4}\{F\cdot F\}-\displaystyle \frac{4}{3}{FG}=0,\end{eqnarray}$
where G = g1I + g2Σ. In componentwise we have $\begin{eqnarray}\begin{array}{l}(16{D}_{x}{D}_{t}+{D}_{x}^{6})\{{f}_{1}\cdot {f}_{1}+\sigma {f}_{2}\cdot {f}_{2}\}\\ +20{D}_{x}^{2}\{{f}_{1}\cdot {g}_{1}+\sigma {f}_{2}\cdot {g}_{2}\}=0,\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}(16{D}_{x}{D}_{t}+{D}_{x}^{6})\{{f}_{1}\cdot {f}_{2}+{f}_{2}\cdot {f}_{1}\}\\ +20{D}_{x}^{2}\{{f}_{2}\cdot {g}_{1}+{f}_{1}\cdot {g}_{2}\}=0,\end{array}\end{eqnarray}$
$\begin{eqnarray}{D}_{x}^{4}\{{f}_{1}\cdot {f}_{1}+\sigma {f}_{2}\cdot {f}_{2}\}-\displaystyle \frac{4}{3}({f}_{1}{g}_{1}+\sigma {f}_{2}{g}_{2})=0,\end{eqnarray}$
$\begin{eqnarray}{D}_{x}^{4}\{{f}_{2}\cdot {f}_{1}+{f}_{1}\cdot {f}_{2}\}-\displaystyle \frac{4}{3}({f}_{2}{g}_{1}+{f}_{1}{g}_{2})=0.\end{eqnarray}$
To obtain one-soliton solution of the system ( $\begin{eqnarray}\begin{array}{l}{\alpha }_{0}=\displaystyle \frac{{\alpha }_{3}(\sigma {\alpha }_{4}^{2}+{\alpha }_{1}^{2})}{2{\alpha }_{1}{\alpha }_{4}},\,{\alpha }_{2}=\displaystyle \frac{{\alpha }_{1}{\alpha }_{4}}{8{\alpha }_{3}},\\ {\alpha }_{5}=\displaystyle \frac{3}{2}{\alpha }_{1}{k}_{1}^{4},\,{\alpha }_{6}=\displaystyle \frac{3}{2}{\alpha }_{4}{k}_{1}^{4}.\end{array}\end{eqnarray}$
Hence one-soliton solution of the KK system ( $\begin{eqnarray}u=\displaystyle \frac{{W}_{1}}{{W}_{2}},\quad v=\displaystyle \frac{{W}_{3}}{{W}_{2}},\end{eqnarray}$
where $\begin{eqnarray}\begin{array}{rcl}{W}_{1} & = & -12{k}_{1}^{2}{\alpha }_{1}^{2}{\alpha }_{3}{\alpha }_{4}\left[32{\alpha }_{3}^{5}{\alpha }_{4}(7\sigma {\alpha }_{4}^{2}-9{\alpha }_{1}^{2}){\left(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2}\right)}^{2}{{\rm{e}}}^{{\theta }_{1}}\right.\\ & & -16{\alpha }_{1}^{2}{\alpha }_{3}^{4}{\alpha }_{4}^{2}(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2})(23\sigma {\alpha }_{4}^{2}-27{\alpha }_{1}^{2}){{\rm{e}}}^{2{\theta }_{1}}\\ & & -16{\alpha }_{1}^{2}{\alpha }_{3}^{3}{\alpha }_{4}^{3}(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2})(\sigma {\alpha }_{4}^{2}-17{\alpha }_{1}^{2}){{\rm{e}}}^{3{\theta }_{1}}\\ & & +4{\alpha }_{1}^{4}{\alpha }_{3}^{2}{\alpha }_{4}^{4}(23\sigma {\alpha }_{4}^{2}-27{\alpha }_{1}^{2}){{\rm{e}}}^{4{\theta }_{1}}\\ & & +2{\alpha }_{1}^{4}{\alpha }_{3}{\alpha }_{4}^{5}(7\sigma {\alpha }_{4}^{2}-9{\alpha }_{1}^{2}){{\rm{e}}}^{5{\theta }_{1}}-{\alpha }_{4}^{6}{\alpha }_{1}^{6}{{\rm{e}}}^{6{\theta }_{1}}\\ & & \left.+64{\alpha }_{3}^{6}{\left(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2}\right)}^{3}\right],\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{W}_{2} & = & \left[64{\alpha }_{1}^{2}{\alpha }_{3}^{3}{\alpha }_{4}(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2})+8{\alpha }_{1}^{2}{\alpha }_{3}^{2}{\alpha }_{4}^{2}(7\sigma {\alpha }_{4}^{2}-9{\alpha }_{1}^{2}){{\rm{e}}}^{2{\theta }_{1}}\right.\\ & & -16{\alpha }_{1}^{4}{\alpha }_{4}^{3}{\alpha }_{3}{{\rm{e}}}^{3{\theta }_{1}}-{\alpha }_{4}^{4}{\alpha }_{1}^{4}{{\rm{e}}}^{4{\theta }_{1}}\\ & & {\left.-16{\alpha }_{3}^{4}{\left(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2}\right)}^{2}\right]}^{2},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{W}_{3} & = & -12{k}_{1}^{2}{\alpha }_{4}^{2}{\alpha }_{1}{\alpha }_{3}{{\rm{e}}}^{{\theta }_{1}}\left[64{\alpha }_{1}^{2}{\alpha }_{3}^{2}{\alpha }_{4}{\left(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2}\right)}^{2}{{\rm{e}}}^{{\theta }_{1}}\right.\\ & & -16{\alpha }_{1}^{2}{\alpha }_{3}^{4}{\alpha }_{4}^{2}(11\sigma {\alpha }_{4}^{2}-7{\alpha }_{1}^{2})(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2}){{\rm{e}}}^{2{\theta }_{1}}\\ & & -4{\alpha }_{1}^{4}{\alpha }_{3}^{2}{\alpha }_{4}^{2}(11\sigma {\alpha }_{4}^{2}-7{\alpha }_{1}^{2}){{\rm{e}}}^{4{\theta }_{1}}-4{\alpha }_{1}^{6}{\alpha }_{4}^{5}{\alpha }_{3}{{\rm{e}}}^{5{\theta }_{1}}\\ & & \left.-{\alpha }_{4}^{6}{\alpha }_{1}^{6}{{\rm{e}}}^{6{\theta }_{1}}-64{\alpha }_{3}^{6}{\left(\sigma {\alpha }_{4}^{2}-{\alpha }_{1}^{2}\right)}^{3}\right],\end{array}\end{eqnarray}$
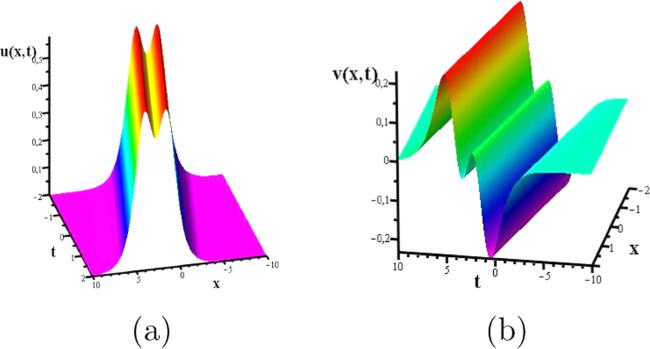
where ${\theta }_{1}={k}_{1}x-{k}_{1}^{5}t+{\delta }_{1}$.Consider the particular values for the parameters of the solution (
$\begin{eqnarray}\begin{array}{rcl}u(x,t) & = & 24{{\rm{e}}}^{x-t}\left[59200{{\rm{e}}}^{x-t}+38080{{\rm{e}}}^{2x-2t}\right.\\ & & +\,13440{{\rm{e}}}^{3x-3t}+7616{{\rm{e}}}^{4x-4t}\\ & & \left.+\,2368{{\rm{e}}}^{5x-5t}+64{{\rm{e}}}^{6x-6t}+8000\right]/\left[640{{\rm{e}}}^{x-t}+1184{{\rm{e}}}^{2x-2t}\right.\\ & & {\left.+\,128{{\rm{e}}}^{3x-3t}+16{{\rm{e}}}^{4x-4t}+400\right]}^{2},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}v(x,t) & = & -48{{\rm{e}}}^{x-t}\left[3200{{\rm{e}}}^{x-t}-16320{{\rm{e}}}^{2x-2t}\right.\\ & & \left.+3264{{\rm{e}}}^{4x-4t}-128{{\rm{e}}}^{5x-5t}-64{{\rm{e}}}^{6x-6t}+8000\right]\\ & & /{\left[640{{\rm{e}}}^{x-t}+1184{{\rm{e}}}^{2x-2t}+128{{\rm{e}}}^{3x-3t}+16{{\rm{e}}}^{4x-4t}+400\right]}^{2}.\end{array}\end{eqnarray}$
The graphs of the above solutions are given in figure 2.
Figure 2. One-soliton solution (u(x, t), v(x, t)) of the KK system ( |
We note that taking different expansions for the functions f1 and f2 in (
Since the expressions are quite longer we shall not display two- and three-soliton solutions of the SK and KK systems here. The more interesting case is the soliton solutions of the nonlocal SK and KK equations presented in section 3 . They can be easily obtained by using the above soliton solutions of the systems with the reduction formulas (1).a, (1).b, (2).a, and (2).b presented in section 3 . These equations will restrict parameters in the soliton solutions (5.7 ) and (5.23 ). We shall discuss two- and three-soliton solutions of the SK and KK systems and soliton solutions of the nonlocal SK and KK equations in a forthcoming publication.
6. Concluding remarks
Integrable nonlinear partial differential equations form a special subclass of partial differential equations. They possess Lax pairs which allow the Cauchy problem to be solved by the application of the inverse scattering transform. They possess infinitely many generalized symmetries which imply the existence of a recursion operator. They possess a bi-Hamiltonian structure which indicates the existence of infinitely many conserved quantities. Hence it is an active research area to obtain new integrable equations. There are certain methods for this purpose. For example one of them is the zero curvature formalism and the other one is the prolongation structures. Here in this paper we proposed commuting algebras to produce systems of integrable equations from scalar integrable equations.
We obtained systems of integrable equations with their recursion operators from scalar integrable equations by applying ${{ \mathcal M }}_{2}$-extension. We used this method for SK and KK equations and obtained the SK system and KK system of equations, respectively. Applying the nonlocal reductions to the symmetrical versions of SK and KK systems we obtained eight different new standard nonlocal and eight different new shifted nonlocal integrable differential equations. We also presented one-soliton solutions for the SK and KK systems.