1. Introduction
The photon is an ideal carrier of energy and information due to its fast velocity and low dissipation. Meanwhile, unlike the electric charge, there is no interaction between photons and it is impossible to control the state of a photon directly by another photon. One of the approaches to tackle this issue is to construct a quantum network [1–3], which is composed of channels and nodes. In such a way, the traveling photons in the channels can be controlled and stored coherently by the quantum matter (such as atoms or artificial atoms) in the nodes.
The waveguide quantum electrodynamical system is a promising platform for realizing the quantum network. The optical fiber with linear dispersion relation is one type of waveguide [4–7] which can be easily coupled to the whispering-gallery-mode resonators, and is widely used in quantum sensing and precise measurement. On the other hand, the coupled resonator waveguide (CRW) [8–12] which supplies the cosine type dispersion relation is also attracting more and more interest in the field of quantum simulation and controlling of photon transport. The reason comes from two aspects, one is that the coupled resonator waveguide supports an energy band, which possesses both the continue band and the band gap regime in the energy domain. The other is that the atom-waveguide system can form the bound state in the gap, which is useful in constructing the functional quantum device.
In the traditional quantum network, the atoms or artificial atoms in the node are usually approximated as point dipoles. However, the successful coherent coupling between the superconducting transmon and the surface acoustic wave brought about the concept of the giant atom [13], in which the phrase ‘giant' means the size of the transmon is comparable to the wavelength of the surface acoustic wave. Therefore, the dipole approximation is broken in the giant atom setup and one has to consider that the artificial atom interacts with the waveguide via multiple coupling points nonlocally. Recently, the giant atom scenario was also realized experimentally by coupling the superconducting qubits [14–16] or magnon ensemble [17] to the curved transmission line and demonstrated the electromagnetic-induced transparency and atomic decoherence-free interaction [18–20]. Theoretically, people have also studied lots of exotic phenomena, which are peculiar to giant atoms, such as frequency-dependent relaxation [21, 22], chiral emission [23, 24], non-Markovian retardation effect [25–32], topological dynamics [33–35] and so on. Specifically, single-photon scattering by the giant atom is investigated deeply by aiming to design photon devices [36–39].
Since the small atom and giant atom can be both used to manipulate the single-photon transport in the waveguide, it is then natural to study how the interplay between the small and giant atom regulates the photonic transmission and reflection in a one-dimensional waveguide. In this paper, we choose the coupled resonator waveguide to supply a propagating channel for the photon with a finite band structure and set the small atom to be a neighbor to one leg of the giant atom to study the photonic scattering. In the resonant case, we show the interference effect induced wide reflection peak. The peak is further widened to a flat widow in the non-resonate case, which is also characterized by the asymmetry Fano line shape.
2. Model
As shown in figure 1, the system we are considering is composed of two two-level atoms and a CRW with infinite length. The first atom is a traditional small atom, which couples to the CRW at the −1th resonator while the second atom is a giant atom, which couples to the CRW via the 0th and the Nth resonators. The Hamiltonian of the CRW is written as (here and after, we set ℏ = 1)
$\begin{eqnarray}{H}_{c}={\omega }_{c}\displaystyle \sum _{j}{a}_{j}^{\dagger }{a}_{j}-\xi \displaystyle \sum _{j}({a}_{j+1}^{\dagger }{a}_{j}+{a}_{j}^{\dagger }{a}_{j+1}),\end{eqnarray}$
where ωc is the bare frequency of the resonators in the CRW and aj is the annihilate operator of the jth resonator. ξ is the hopping strength between the nearest resonators.
Figure 1. Schematic configuration for a one-dimensional coupled resonator waveguide coupled to a small atom and a giant atom simultaneously. Here, the giant atom couples to the waveguide via the 0th and Nth sites while the small atom is located in the −1th resonator. |
Coupling the small and giant atoms to the CRW, the Hamiltonian of the whole system is expressed as
$\begin{eqnarray}\begin{array}{rcl}H & = & {H}_{c}+\displaystyle \sum _{l=1,2}{{\rm{\Omega }}}_{l}| e{\rangle }_{l}\langle e| \\ & & +[{J}_{1}{a}_{-1}^{\dagger }{\sigma }_{1}^{-}+{J}_{2}({a}_{0}^{\dagger }+{a}_{N}^{\dagger }){\sigma }_{2}^{-}+{\rm{H}}.{\rm{c}}.],\end{array}\end{eqnarray}$
where Ω1 and Ω2 are the resonant frequencies of the small and giant atoms, respectively, between the excited state ∣e⟩ and ground state ∣g⟩, ${\sigma }_{1}^{-}={\left({\sigma }_{1}^{+}\right)}^{\dagger }=| g{\rangle }_{1}\langle e| $ and ${\sigma }_{2}^{-}={\left({\sigma }_{2}^{+}\right)}^{\dagger }\,=| g{\rangle }_{2}\langle e| $ are the corresponding lower operators. J1(2) is the coupling strength between the small (giant) atom and the CRW. Here, we have performed the rotation wave approximation in the atom–CRW interaction.3. Single-photon scattering
Since the excitation is conserved in our system under the rotating wave approximation, we can investigate the single-photon state to demonstrate how to control the photons by the atoms. To this end, we assume the wave function in the single excitation subspace as
$\begin{eqnarray}| \psi \rangle =\left(\displaystyle \sum _{j}{c}_{j}{a}_{j}^{\dagger }+{u}_{1e}{\sigma }_{1}^{+}+{u}_{2e}{\sigma }_{2}^{+}\right)| 0,g,g\rangle ,\end{eqnarray}$
where ∣0, g, g⟩ represents that all of the resonators in the waveguide are in their vacuum states while both the small and giant atoms are in their ground states. cj is the amplitude for finding a photon in the jth resonator, while u1(2)e is the excitation amplitude for the small (giant) atom.We now consider that a single photon with wave vector k is incident from the left side of the waveguide, it will be scattered by both of the small and giant atoms and cj can be expressed as
$\begin{eqnarray}{c}_{j}=\left\{\begin{array}{cc}{{\rm{e}}}^{{\rm{i}}{kj}}+{r{\rm{e}}}^{-{\rm{i}}{kj}} & j\lt -1\\ {A{\rm{e}}}^{{\rm{i}}{kj}}+{B{\rm{e}}}^{-{\rm{i}}{kj}} & 0\leqslant j\leqslant N\\ {t{\rm{e}}}^{{\rm{i}}{kj}} & j\gt N\end{array}\right..\end{eqnarray}$
The above equation demonstrates the propagation process of the incident photon in the waveguide: when the photon arrives at the −1th resonator, it will interact with the small and giant atoms. As a result, it will be reflected with an amplitude r and transmitted with the amplitude A. Then, the transmitted photon will continue to travel rightward in the regime covered by the giant atom until it meets the right leg of the giant atom at the Nth resonator. Then, the photon will be transmitted with amplitude t and reflected with amplitude B.In the regime of j ≠ − 1, 0, N, we can obtain the dispersion relation $E={\omega }_{c}-2\xi \cos k$. It means that the CRW supports a continuous band centered at ωc with a width of 4ξ. In other words, only the photon that carries the frequency in the regime of ω ∈ [ωc − 2ξ, ωc + 2ξ] can propagate along the waveguide. Furthermore, at the atom-waveguide coupling site of j = N, by use of the continuous condition AeikN + Be−ikN = teikN and after some detailed calculations, we will obtain the reflection amplitude
$\begin{eqnarray}r=\displaystyle \frac{-{J}_{1}^{2}Q\xi {{\rm{\Delta }}}_{2}{{\rm{e}}}^{-2{\rm{i}}k}-{J}_{2}^{2}Q\xi {{\rm{\Delta }}}_{1}{W}^{2}-{J}^{2}W\left(W-2{{\rm{e}}}^{-2{\rm{i}}k}\right)}{Q\xi \left({J}_{1}^{2}{{\rm{\Delta }}}_{2}+2{J}_{2}^{2}{{\rm{\Delta }}}_{1}W-\xi {{\rm{\Delta }}}_{1}{{\rm{\Delta }}}_{2}Q\right)+{J}^{2}\left[{{\rm{e}}}^{2{\rm{i}}k(1+N)}+Q{{\rm{e}}}^{{\rm{i}}k}\left(2{{\rm{e}}}^{{\rm{i}}{kN}}+1\right)-1\right]},\end{eqnarray}$
where $J={J}_{1}{J}_{2},Q=2\mathrm{isin}k,W=1+{{\rm{e}}}^{{\rm{i}}{kN}}$. Δ1(2) = E − Ω1(2) is the detuning between the small (giant) atom and the propagating photons in the waveguide.By setting J1(2) = 0, the above equation reproduces the results of a single giant (small) atom. In what follows, we will demonstrate that the single-photon scattering behavior is dramatically affected by the atoms–waveguide couplings, and the small–giant atom hybrid setup is more flexible for designing and manipulating the quantum devices.
4. Resonance scattering
In this section, we consider the resonance case of Ω1 = Ω2 = ωc, such that Δ1 = Δ2 = Δ. In this case, the photon with frequency Δ = 0 will be completely reflected, completely transmitted and half transmitted by the atom when the size of atom N = 4m, 4m + 2, 2m + 1, m = 0, 1, 2 ⋯ (N = 0 corresponds to the small atom setup). For our small–giant atom hybrid system, we plot the reflection rate R = ∣r∣2 as a function of the detuning Δ in figure 2.
Figure 2. The single-photon reflection rate when both the small and giant atoms are resonant with the bare resonator in the waveguide. The parameters are set as ωc = Ω1 = Ω2 = 20ξ, J1 = 0.4ξ and N = 2, 3, 4 for panels (a), (b), and (c), respectively. |
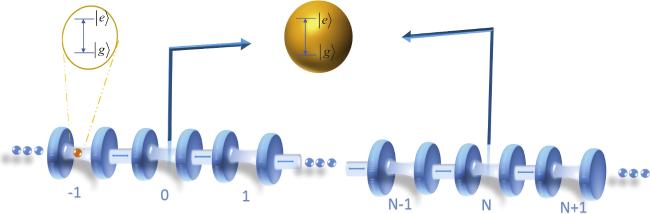
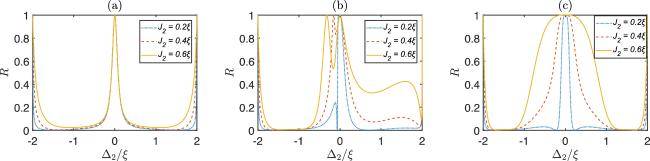
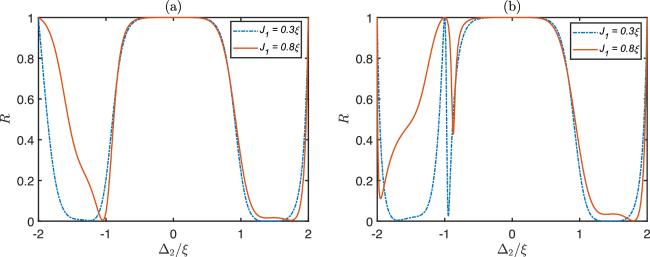
As shown in figure 2, we plot the photonic reflection rate for N = 2, 3, 4, respectively. For N = 2, the incident photon will be completely transmitted when it is resonant with the bare frequency of the resonators in the waveguide. However, we observe in figure 2(a) that it is reflected. Furthermore, the width of the reflection peak at Δ = 0 is independent of the coupling strength between the giant atom and the waveguide. In contrast, this coupling plays a significant role for N=3,4, in which case the small atom induces the complete reflection near the regime of Δ = 0. For the case of N = 3, the giant atom gives birth to a Lamb shift, which is verified by the reflection rate in the regime of Δ < 0 with a relatively larger J2, as shown in figure 2(b). On the other hand, when the small atom couples to the waveguide stronger than that of the giant atom (J1 = 0.4ξ, J2 = 0.2ξ), we find a deep valley, which is accompanied by an asymmetric Fano shape. Moving the case of N = 4, both the small and the giant atoms will reflect the resonant incident photon as shown in figure 2(c). Here, the giant atom coupling actually widens the reflection peak and is beneficial to construct the photon device.
5. Off-resonance scattering
In the previous section, we studied the controllable single-photon scattering in the CRW when the giant atom is resonant with the small atom. As a natural development, we now investigate the case when the small atom is detuned from the giant atom. Here, we regard the small atom as a dressed element in the giant atom–CRW (GACRW) coupled system. Therefore, it is beneficial to analyze the energy spectrum of the GACRW. As shown in figure 3, we plot the spectrum in the single excitation subspace for N = 4, the system supports a continual band in the regime of ωc − 2ξ < E < ωc + 2ξ. In addition, we can also observe a pair of the bound states, which are located below and above the continuum band, respectively.
Figure 3. The energy spectrum of the giant atom-waveguide coupled system in the single excitation space. The parameters are set as Ω2 = ωc = 20ξ, J1 = 0. |
We plot the single-photon reflection rate when the frequency of the small atom is resonant with the bound state (Ω1 = 17.91ξ) and is inside the continuum band (Ω1 = 19ξ) of the GACAW coupled system, respectively, in figure 4(a) and (b), respectively. In both cases, we observe a wide complete reflection window near the regime of Δ2 = 0 with a width being achieved by 1.5ξ − 2ξ. In our consideration, the frequency of the small atom is lower than that of the giant atom and the bare frequency of the resonator. Under the considered parameter, we can also find a transmission widow (R ≈ 0) near the upper boundary of the continuum band in the regime of Δ2 ≈ 1.5ξ with a width of 0.5ξ. Moreover, as shown in the figure, the width of the reflected and transmitted window is nearly independent of the coupling strength of the small atom. In the recent experiment setups, most of the giant atom models can be constructed by the superconducting transmon qubit. In such a physical platform, the photonic hopping strength in the waveguide can reach ξ ≈ 100 MHz [14–16], therefore, the width of the reflection and transmission windows can be achieved by 200 MHz and 50 MHz, respectively. In this sense, it is therefore beneficial to design the single-photon device, to realize a wide-band photonic reflection or transmission.
Figure 4. The single-photon reflection rate when the small atom is detuned from the giant atom. The parameters are set as Ω2 = Ωc = 20ξ, J2 = 0.7ξ and N = 4. In panel (a), we have set the small atom as resonant with the lower bound state of the giant atom-waveguide coupled system, that is Ω1 = 17.91ξ. In panel (b), we have set to small atom to be in the continuum band of the atom-waveguide coupled system, that is, Ω1 = 19ξ. |
It is more plausible to find the exotic behavior when the incident photon is red detuning from the giant atom (Δ2 < 0). Nearby, in the regime of Δ2 ≈ − 1.5ξ, we find that the incident photon will be transmitted (R ≈ 0) when the coupling is relatively small (for example J1 = 0.3ξ). However, for the stronger coupling case (J1 = 0.8ξ), we can only observe a narrow valley in figure 4(a), where the frequency of the small atom is outside the continual band. On the other hand, as the small atom is set to be inside the continual band, we interestingly find the Fano shape as shown by the red curve in figure 4(b) and the complete reflection occurs exactly at the frequency of E = Ω2 (Δ2 = − ξ). This phenomenon can be explained by the energy spectrum in figure 3. The GACAW coupled system provides a continuum band, and the small atom with Ω2 = 19ξ provides a discrete energy level. When the incident photon carries a frequency within the continual band and is resonant with the discrete level, it will be completely reflected and lead to a Fano scattering line shape.
6. Conclusions
In this paper, we have investigated single-photon scattering in a one-dimensional CRW which is dressed by a giant atom and a small atom. Within the current technology, the considered setup can be realized by superconducting circuits. Here, the giant atom can be implemented by the transmon to be coupled to the waveguide via two sites with the assistance of capacitance or inductance. The photonic hopping strength between the neighbor resonators in the waveguide can be achieved by hundreds of MHz [40, 41], and the atom-waveguide coupling strength is in the regime of tens to hundreds of MHz, and the intrinsic dissipation of the superconducting artificial atom can be two orders smaller than the above hopping or coupling strength and is neglected in our investigations.
In conclusion, we find that the scattering line shape and the reflection (transmission) can be manipulated on demand in a small atom-giant atom hybrid system. When the small atom is resonant with the giant atom, the small atom will induce the complete reflection for the arbitrary geometric configuration of the giant atom. In the off-resonance case, we find the discrete-continual energy level diagram-induced Fano line shape. We hope our results on the scattering are helpful to the designing of a coherent photonic device, to realize the wide band reflection or transmission.