1. Introduction
Entanglement is a remarkable phenomenon in quantum mechanics, serving as a vital resource for quantum information processing and communication [1–4]. Significant progresses have been achieved in understanding the roles played by the entanglement in quantum tasks such as quantum teleportation [5], quantum key distribution [6] and quantum computing [7].
The monogamy of entanglement (MoE) is a distinguishing feature of entanglement that sets it apart from classical correlations [8, 9]. A subsystem entangled with one party cannot freely share its entanglement with other parties of the whole system. Since MoE imposes limitations on the potential information accessible to an eavesdropper for extracting the secret key, it holds immense significance in securing various information-theoretic protocols like quantum key distribution [10–12]. MoE has also been widely studied in many areas of quantum physics such as quantum information theory [13], condensed-matter physics [14] and even black-hole physics [15].
MoE manifests itself quantitatively in the form of mathematical inequalities. Coffman, Kundu and Wootters (CKW) first characterized the monogamy of an entanglement measure ${ \mathcal E }$ for a three-qubit states ρABC [8], known as the CKW inequality,1 ) provides a lower bound for ‘one-to-group' entanglement, termed as quantum marginal entanglements [25].
$\begin{eqnarray}{ \mathcal E }({\rho }_{A| {BC}})\geqslant { \mathcal E }({\rho }_{{AB}})+{ \mathcal E }({\rho }_{{AC}}),\end{eqnarray}$
where ${\rho }_{{AB}}={\mathrm{tr}}_{C}({\rho }_{{ABC}})$, ${\rho }_{{AC}}={\mathrm{tr}}_{B}({\rho }_{{ABC}})$ are the reduced density matrices of ρABC, ${ \mathcal E }({\rho }_{A| {BC}})$ stands for the entanglement under the bipartition A and BC. Subsequently, Osborne and Verstraete further extend the monogamy inequality by incorporating the squared concurrence for any n-qubit systems [16]. Since then considerable research has been conducted on MoE by focusing on various entanglement measures such as the squared entanglement of formation (EoF) [17–19], the squared Rényi-α entropy [20], the squared Tsallis-q entropy [21] and the squared Unified-(r, s) entropy [22]. Studies on monogamy inequalities based on the αth power of entanglement measures for multiqubit systems have been given in [21, 23, 24]. The traditional monogamy inequality (Generally, the relation (1 ) may not hold for multi-qudit systems. In [19, 26, 27] the authors presented counter examples in higher-dimensional systems. There are even additive entanglement measures that do not satisfy any nontrivial monogamous relations in multipartite higher-dimensional systems [28]. Up to now, it appears that only one known entanglement measure, the squashed entanglement, is monogamous for arbitrary dimensional systems [29]. Due to the importance of the study on monogamy relations for higher-dimensional multipartite systems, it is natural to explore the monogamy inequalities for higher-dimensional multipartite states.
With respect to higher-dimensional quantum states, Kim and Sanders extended the GW state from n-qubit to n-qudit systems in 2008, demonstrating that the GW states adhere to the monogamy inequality in terms of squared concurrence [27]. In 2015, Choi and Kim showed that a superposition of the generalized W-class states and the vacuum states (GWV) satisfy the strong monogamy inequality in terms of the squared convex roof extended negativity [30]. In 2016, Kim showed that a partially coherent superposition of a GW state and the vacuum saturates the strong monogamy inequality [31]. In 2020, Shi and Chen presented the monogamy inequalities beyond qubits by using the Tsallis-q entanglement for the GW states [32]. Then, Liang et al adopted a similar methodology to extend the monogamy relations from Tsallis-q entanglement to Rényi-α entanglement for the GWV states [33]. Furthermore, Li et al have recently introduced monogamy relations for multi-qudit GW states by using the unified-(q, s) entanglement [34]. Motivated by these significant advancements, our research aims to further investigate MoE for GW states with arbitrary partitions in higher-dimensional quantum systems.
The unified-(q, s) entanglement is a two-parametric generalization of the entanglement of formation. For selective choices of the two parameters q and s, other entanglement measures such as concurrence, entanglement of formation, Tsallis-q entanglement and Rényi-α entanglement can be regarded as the special cases of the unified-(q, s) entanglement [35]. It has been proven that the unified-(q, s) entanglement satisfies the CKW inequality (1 ) and its dual inequality [35, 36]. Khan et al presented the monogamy relation based on the squared unified-(q, s) for arbitrary multi-qubit mixed states in the extended (q, s) region [22]. In [37], the authors provided universal entanglement distribution inequalities for multipartite higher-dimensional pure states by utilizing the unified-(q, s) entanglement.
In [38], the authors introduced two partition-dependent residual entanglements (PREs) based on the negativity for several typical multi-qubit states. Furthermore, the authors demonstrated the unique utility of PREs in analyzing the entanglement dynamics of multi-qubit systems, particularly in processing qubit blocks and sub-blocks. PREs can facilitate a comprehensive comprehension of the entanglement dynamics exhibited by GW states with different levels and formats of partitions.
There has been ample quantitative research and characterization of the restricted shareability for multi-qubit entanglement. However, the understanding of entanglement distribution in higher-dimensional systems is still limited and requires further investigation. In this paper, we consider the monogamy relations of the unified-(q, s) entanglement (UE) in higher-dimensional systems. This article is organized as follows. In section 2 , we briefly introduce a few definitions of entanglement measures, as well as an overview of the GW states. In section 3 , we first provide the extended (q, s) region of the generalized analytic formula of UE. By using the analytical formula, the monogamy relation based on the squared UE for qudit GW states is presented. In section 4 , in order to provide a more precise description of the entanglement distribution of GW states, we delve into tighter monogamy relations based on the αth (α ≥ 2) power of UE. In section 5 , for n-qudit systems ABC1...CN−2, generalized monogamy relation and upper bound satisfied by the βth (0 ≤ β ≤ 1) power of UE for the GW states under the partition AB and C1...CN−2 are established. Moreover, in section 6 , we explore the applications of our results in PREs, and offer valuable insights into the study of entanglement dynamics for GW states. Finally, a conclusion is made in section 7 .
2. Preliminaries
We recall some relevant entanglement measures and introduce the concept of GW states. Let HA and HB denote a finite dimensional complex inner product vector space associated with quantum subsystems A and B, respectively. For a bipartite pure state ∣ψ⟩AB ∈ HA ⨂ HB, the concurrence C(∣ψ⟩AB) is defined by [39]
$\begin{eqnarray}C(| \psi {\rangle }_{{AB}})=\sqrt{2[1-\mathrm{tr}({\rho }_{A}^{2})]},\end{eqnarray}$
where ${\rho }_{A}={\mathrm{tr}}_{B}(| \psi {\rangle }_{{AB}}\langle \psi | )$ is the reduced density matrix of subsystem A. For any mixed state ρAB ∈ HA ⨂ HB, the concurrence is given via the convex roof extension $\begin{eqnarray}C({\rho }_{{AB}})=\mathop{\min }\limits_{\{{p}_{i},| {\psi }_{i}\rangle \}}\displaystyle \sum _{i}{p}_{i}C(| {\psi }_{i}\rangle ),\end{eqnarray}$
where the minimum is taken over all possible pure decompositions of ρAB = ∑ipi∣ψi⟩AB⟨ψi∣.For a bipartite pure state ∣ψ⟩AB ∈ HA ⨂ HB, the unified-(q, s) entanglement is given by
$\begin{eqnarray}{U}_{q,s}\left(| \psi {\rangle }_{{AB}}\right)={U}_{q,s}({\rho }_{A})=\displaystyle \frac{1}{(1-q)s}\left[{\left(\mathrm{tr}{\rho }^{q}\right)}^{s}-1\right].\end{eqnarray}$
For a mixed state ρAB, the unified-(q,s) entanglement is given via the convex-roof extension [35], $\begin{eqnarray}{U}_{q,s}\left({\rho }_{{AB}}\right):= \min \displaystyle \sum _{i}{p}_{i}{U}_{q,s}({\left|{\psi }_{i}\right\rangle }_{{AB}}),\end{eqnarray}$
with the minimum taking over all possible pure state decompositions of ${\rho }_{{AB}}={\sum }_{i}{p}_{i}{\left|{\psi }_{i}\right\rangle }_{{AB}}\left\langle {\psi }_{i}\right|$.As the unified-(q,s) entropy converges to the Rényi-α and Tsallis-q entropies when s tends to 0 and 1, respectively, one has
$\begin{eqnarray}\mathop{\mathrm{lim}}\limits_{s\to 0}{U}_{q,s}\left({\rho }_{{AB}}\right)={{ \mathcal R }}_{\alpha }\left({\rho }_{{AB}}\right),\end{eqnarray}$
where ${{ \mathcal R }}_{\alpha }\left({\rho }_{{AB}}\right)$ is the Rényi-α (α = q) entanglement of ρAB, and $\begin{eqnarray}\mathop{\mathrm{lim}}\limits_{s\to 1}{U}_{q,s}\left({\rho }_{{AB}}\right)={{ \mathcal T }}_{q}\left({\rho }_{{AB}}\right),\end{eqnarray}$
where ${{ \mathcal T }}_{q}\left({\rho }_{{AB}}\right)$ is the Tsallis-q entanglement of ρAB. When q tends to 1, $\begin{eqnarray}\mathop{\mathrm{lim}}\limits_{q\to 1}{U}_{q,s}\left({\rho }_{{AB}}\right)={E}_{f}\left({\rho }_{{AB}}\right),\end{eqnarray}$
where Ef(ρAB) is the EoF of ρAB. Thus unified-(q,s) entanglement is a two-parameter generalization of EoF.Moreover, for a bipartite pure state ∣ψ⟩AB with Schmidt-rank 2, we have
$\begin{eqnarray}{U}_{\tfrac{1}{2},2}\left({\rho }_{{AB}}\right)=C\left({\rho }_{{AB}}\right),\end{eqnarray}$
for $q=\tfrac{1}{2}$ and s = 2, and $\begin{eqnarray}{U}_{\mathrm{2,1}}\left({\rho }_{{AB}}\right)=\displaystyle \frac{1}{2}{C}^{2}\left({\rho }_{{AB}}\right),\end{eqnarray}$
for q = 2 and s = 1.For any two-qubit mixed state and any bipartite pure state with Schmidt-rank 2, one has [36]
$\begin{eqnarray}{U}_{q,s}\left({\left|\psi \right\rangle }_{{AB}}\right)={f}_{q,s}\left(C({\left|\psi \right\rangle }_{{AB}})\right),\end{eqnarray}$
where fq,s(x) is a differential function, $\begin{eqnarray}{f}_{q,s}(x)=\displaystyle \frac{{\left({\left(1+\sqrt{1-{x}^{2}}\right)}^{q}+{\left(1-\sqrt{1-{x}^{2}}\right)}^{q}\right)}^{s}-{2}^{{qs}}}{(1-q)s{2}^{{qs}}},\end{eqnarray}$
with q ≥ 1, 0 ≤ s ≤ 1 and qs ≤ 3.Based on an extended (q, s)-region with $q\geqslant (\sqrt{9{s}^{2}-24s+28}-(2+3s))/(2(2-3s))$, 0 ≤ s ≤ 1, ${qs}\leqslant (5+\sqrt{13})/2$, the authors in [22] proved that the analytic formula (11 ) of the unified-(q, s) entanglement still holds in parameter region14 ) includes n-qubit W-class states in equation (13 ) as a special case of d = 2. The GW state can be viewed as a special case of the coherent superposition of a generalized W-class state and vacuum state (GWV),
$\begin{eqnarray*}{ \mathcal R }=\left\{(q,s)\left|\begin{array}{c}\displaystyle \frac{\sqrt{9{s}^{2}-24s+28}-(2+3s)}{2(2-3s)}\leqslant q,\\ q\leqslant (5+\sqrt{13})/2s,\,0\leqslant s\leqslant 1\end{array}\right.\right\}.\end{eqnarray*}$
The n-qubit W-class states and n-qudit GW states are given by [27] $\begin{eqnarray}\begin{array}{l}{\left|W\right\rangle }_{{A}_{1}{A}_{2}...{A}_{n}}\\ =\,{a}_{1}\left|10\cdots 0\right\rangle +{a}_{2}\left|01\cdots 0\right\rangle \,+...+\,{a}_{n}\left|00\cdots 1\right\rangle ,\end{array}\end{eqnarray}$
and $\begin{eqnarray}\begin{array}{l}{\left|{W}_{n}^{d}\right\rangle }_{{A}_{1}\cdots {A}_{n}}\\ =\,\displaystyle \sum _{i=1}^{d-1}({a}_{1i}\left|i0\cdots 0\right\rangle +{a}_{2i}\left|0i\cdots 0\right\rangle \,+\cdots +\,{a}_{{ni}}\left|00\cdots 0i\right\rangle ),\end{array}\end{eqnarray}$
with the normalization conditions ${\sum }_{i=1}^{n}| {a}_{i}{| }^{2}=1$ and ${\sum }_{s=1}^{n}{\sum }_{i=1}^{d-1}| {a}_{{si}}{| }^{2}=1$, respectively. Equation ( $\begin{eqnarray}\begin{array}{rcl}{\left|\varphi \right\rangle }_{{A}_{1}{A}_{2}...{A}_{n}} & = & \sqrt{p}{\left|{W}_{n}^{d}\right\rangle }_{{A}_{1}\cdots {A}_{n}}\\ & & +\sqrt{1-p}{\left|0\right\rangle }_{{A}_{1}\cdots {A}_{n}}^{\otimes n},\end{array}\end{eqnarray}$
where 0 ≤ p ≤ 1.3. Monogamy of the unified-(q, s) entanglement
Consider an n-qudit GW state ${\left|{W}_{n}^{d}\right\rangle }_{{A}_{1}\cdots {A}_{n}}$ given in (14 ). We first present a functional relation between UE and concurrence, from which we derive the related monogamy relations. We need the following lemmas.
[Lemma 1]. [22] The function fq,s(C) with $(q,s)\in { \mathcal R }$ is a monotonically increasing and convex function of concurrence C.
Set y2 = x and denote gq,s(y2) = fq,s(x). Then for any two-qubit mixed states and any bipartite pure states with Schmidt-rank 2, equations (11 ) and (12 ) can be rephrased as
$\begin{eqnarray}{U}_{q,s}\left({\left|\psi \right\rangle }_{{AB}}\right)={g}_{q,s}\left({C}^{2}({\left|\psi \right\rangle }_{{AB}})\right),\end{eqnarray}$
where $(q,s)\in { \mathcal R }$ and the function gq,s(y) has the form $\begin{eqnarray}{g}_{q,s}(y):= \displaystyle \frac{{\left({\left(1+\sqrt{1-y}\right)}^{q}+{\left(1-\sqrt{1-y}\right)}^{q}\right)}^{s}-{2}^{{qs}}}{(1-q)s{2}^{{qs}}}.\end{eqnarray}$
[Lemma 2]. [22] The function ${g}_{q,s}^{2}({C}^{2})$ with $(q,s)\in { \mathcal R }$ is a monotonically increasing and convex function of the squared concurrence C2.
[Lemma 3]. [30] Let ${\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ be an m-qudit reduced density matrix of the n-qudit GWV state (15 ) ${\left|\varphi \right\rangle }_{{A}_{1}\cdots {A}_{n}}$, 2 ≤ m ≤ n − 1. For any pure state decomposition of ${\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ such that
$\begin{eqnarray}{\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}=\displaystyle \sum _{k}{q}_{k}{\left|{\phi }_{k}\right\rangle }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}\left\langle {\phi }_{k}\right|,\end{eqnarray}$
${\left|{\phi }_{k}\right\rangle }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ is a superposition of an m-qudit generalized W-class state and vacuum.Since each GWV state is a Schmidt-rank 2 pure state under any partition, we see that for any pure state decomposition $\{{p}_{i},{\left|{\phi }_{i}\right\rangle }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{i}}| {A}_{{j}_{i+1}}\cdots {A}_{{j}_{m}}}\}$ of a reduced density matrix ${\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$, ${\left|{\phi }_{i}\right\rangle }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{i}}| {A}_{{j}_{i+1}}\cdots {A}_{{j}_{m}}}$ is a pure state with Schmidt-rank 2. We have the following theorem.
[Theorem 1]. Let ${\rho }_{{A}_{{j}_{1}}\cdots {A}_{{j}_{m}}}$ be a reduced density matrix of an n-qudit GW state given by (14 ). We have
$\begin{eqnarray}{U}_{q,s}^{2}({\rho }_{{A}_{{j}_{1}}| {A}_{{j}_{2}}\cdots {A}_{{j}_{m}}})={g}_{q,s}^{2}({C}^{2}({\rho }_{{A}_{{j}_{1}}| {A}_{{j}_{2}}\cdots {A}_{{j}_{m}}})),\end{eqnarray}$
for $(q,s)\in { \mathcal R }$.For convenience, we denote ${\rho }_{{A}_{{j}_{1}}| {A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ as ${\rho }_{{AB}}$. There exists a pure state decomposition $\{{q}_{i},\left|{\phi }_{i}\right\rangle \}$ such that
$\begin{eqnarray*}C({\rho }_{{AB}})=\displaystyle \sum _{i}{q}_{i}C({\left|{\phi }_{i}\right\rangle }_{{AB}}),\end{eqnarray*}$
in which all $C({\left|{\phi }_{i}\right\rangle }_{{AB}})$ are equal [32]. Hence, we have $\begin{eqnarray}\begin{array}{rcl}{g}_{q,s}^{2}({C}^{2}({\rho }_{{AB}})) & = & {f}_{q,s}^{2}(C({\rho }_{{AB}}))\\ & = & {f}_{q,s}^{2}\left(\displaystyle \sum _{i}{q}_{i}C({\left|{\phi }_{i}\right\rangle }_{{AB}})\right)\\ & = & \displaystyle \sum _{i}{q}_{i}{f}_{q,s}^{2}\left(C({\left|{\phi }_{i}\right\rangle }_{{AB}})\right)\\ & = & \displaystyle \sum _{i}{q}_{i}{U}_{q,s}^{2}\left(C({\left|{\phi }_{i}\right\rangle }_{{AB}})\right)\\ & \geqslant & {U}_{q,s}^{2}({\rho }_{{AB}}),\end{array}\end{eqnarray}$
where the third equality is due to that $C({\left|{\phi }_{i}\right\rangle }_{{AB}})$ are equal for all i, the fourth equality is due to (Next, we prove that ${g}_{q,s}^{2}({C}^{2}({\rho }_{{AB}}))\leqslant {U}_{q,s}^{2}({\rho }_{{AB}})$. Let $\{{p}_{i},\left|{\omega }_{i}\right\rangle \}$ be the optimal pure state decomposition of ${U}_{q,s}({\rho }_{{AB}})$. Then
$\begin{eqnarray}\begin{array}{rcl}{U}_{q,s}^{2}({\rho }_{{AB}}) & = & {\left[\displaystyle \sum _{i}{p}_{i}{U}_{q,s}({\left|{\omega }_{i}\right\rangle }_{{AB}})\right]}^{2}\\ & = & {\left[\displaystyle \sum _{i}{p}_{i}{f}_{q,s}\left(C({\left|{\omega }_{i}\right\rangle }_{{AB}})\right)\right]}^{2}\\ & \geqslant & {\left[{f}_{q,s}(\displaystyle \sum _{i}{p}_{i}C({\left|{\omega }_{i}\right\rangle }_{{AB}}))\right]}^{2}\\ & \geqslant & {f}_{q,s}^{2}(C({\rho }_{{AB}}))\\ & = & {g}_{q,s}^{2}({C}^{2}({\rho }_{{AB}})),\end{array}\end{eqnarray}$
where the second equality is due to (The following lemma will be used to derive the monogamy relation of UE.
[Lemma 4]. [27] For any n-qudit GW states (14 ) and a partition P = {P1,…,Pr} of the subsystems S = {A1, A2,…,An}, r ≤ n, ${C}^{2}({\rho }_{{P}_{s}| {P}_{1}\cdots {\widehat{P}}_{s}\cdots {P}_{r}})={\sum }_{k\ne s}{C}^{2}({\rho }_{{P}_{s}{P}_{k}})={\sum }_{k\ne s}{[{C}^{a}({\rho }_{{P}_{s}{P}_{k}})]}^{2}$ and $C({\rho }_{{P}_{s}{P}_{k}})={C}^{a}({\rho }_{{P}_{s}{P}_{k}})$ for all k ≠ s, where $({P}_{1}\cdots {\widehat{P}}_{s}\cdots {P}_{r})$ denotes that the partite Ps is removed from the partition, ${P}_{s}\cap {P}_{k}=\varnothing $ for s ≠ k and ⋃s Ps = S.
[Theorem 2]. Let ${\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ be the reduced density matrix of an n-qudit GW state (14 ) and {P1, P2, ⋯ ,Pr} a partition of $\{{A}_{{j}_{1}},{A}_{{j}_{2}},\cdots ,{A}_{{j}_{m}}\},$ r ≤ m ≤ n. We have the following monogamy inequality,
$\begin{eqnarray}{U}_{q,s}^{2}({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}})\geqslant \displaystyle \sum _{i=2}^{r}{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{i}}),\end{eqnarray}$
for $(q,s)\in { \mathcal R }$.For $(q,s)\in { \mathcal R }$, we have
$\begin{eqnarray}\begin{array}{rcl}{U}_{q,s}^{2}({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{k}}) & = & {g}_{q,s}^{2}({C}^{2}({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}}))\\ & = & {g}_{q,s}^{2}(\displaystyle \sum _{i=2}^{r}{C}^{2}({\rho }_{{P}_{1}{P}_{i}}))\\ & \geqslant & \displaystyle \sum _{i=2}^{r}{g}_{q,s}^{2}({C}^{2}({\rho }_{{P}_{1}{P}_{i}}))\\ & = & \displaystyle \sum _{i=2}^{r}{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{i}}),\end{array}\end{eqnarray}$
where the first equality is due to theorem 1, the second equality is by lemma 4, the inequality is due to that the function ${g}_{q,s}^{2}({{ \mathcal C }}^{2})$ is a convex function in lemma 2 for $(q,s)\in { \mathcal R }$, and the last equality is obtained by theorem 1.When s tends to 1, (22 ) is reduced to the monogamy inequality of Tsallis-q entanglement given in [32], ${{ \mathcal T }}_{q}^{2}({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}})\geqslant {\sum }_{i\,=\,2}^{r}{{ \mathcal T }}_{q}^{2}({\rho }_{{P}_{1}{P}_{i}})$. When s tends to 0, (22 ) reduces to the monogamy inequality of Rényi-α entanglement, ${{ \mathcal R }}_{\alpha }^{2}({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}})\geqslant {\sum }_{i\,=\,2}^{r}{{ \mathcal R }}_{\alpha }^{2}({\rho }_{{P}_{1}{P}_{i}})$. When q tends to 1, (22 ) reduces to the monogamy inequality of EoF, ${E}_{f}^{2}({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}})\geqslant {\sum }_{i\,=\,2}^{r}{E}_{f}^{2}({\rho }_{{P}_{1}{P}_{i}})$.
Next, we generalize theorem 2 to the α-th power of UE for GW states for α ≥ 2 and α ≤ 0. For r = 3, we can always have ${U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})\leqslant {U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})$ by relabeling the partition {P1, P2, P3}. Therefore, when α ≥ 2 we get
$\begin{eqnarray*}\begin{array}{rcl}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}}) & \geqslant & {\left({U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})+{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})\right)}^{\tfrac{\alpha }{2}}\\ & = & {U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}}){\left(1+\displaystyle \frac{{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})}{{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})}\right)}^{\tfrac{\alpha }{2}}\\ & \geqslant & {U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})+{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}}),\end{array}\end{eqnarray*}$
where we have used theorem 2 in the first inequality. The second inequality is obtained since (1 + t)x≥1 + tx for any real numbers x and t, 0 ≤ t ≤ 1 and x ∈ [1, ∞ ]. When α ≤ 0, we get $\begin{eqnarray*}\begin{array}{rcl}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}}) & \leqslant & {\left({U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})+{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})\right)}^{\tfrac{\alpha }{2}}\\ & = & {U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}}){\left(1+\displaystyle \frac{{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})}{{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})}\right)}^{\tfrac{\alpha }{2}}\\ & \lt & {U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})+{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}}),\end{array}\end{eqnarray*}$
where the first inequality is due to theorem 2. The second inequality is obtained as (1 + t)x<1 + tx for any real numbers x and t, t ≥ 0 and x ∈ [– ∞ , 0]. Therefore, we can have the following conclusion.[Theorem 3]. Let ${\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ be the reduced density matrix of an n-qudit GW state ${\left|\psi \right\rangle }_{{A}_{1}\cdots {A}_{n}}$, and {P1, P2, ⋯ ,Pr} a partition of $\{{A}_{{j}_{1}},{A}_{{j}_{2}},\cdots ,{A}_{{j}_{m}}\}$, r ≤ m ≤ n. For $(q,s)\in { \mathcal R }$ we have
$\begin{eqnarray}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}})\geqslant \displaystyle \sum _{i=2}^{r}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{i}}),\end{eqnarray}$
when α ≥ 2, and $\begin{eqnarray}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}})\lt \displaystyle \sum _{i=2}^{r}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{i}}),\end{eqnarray}$
when α ≤ 0.4. Tighter monogamy inequalities in terms of UE
The refined monogamy relations yield more precise characterizations of entanglement distributions, which are intimately connected to the security of quantum cryptographic protocols [10] based on entanglement. Therefore, gaining tighter entanglement monogamy relations is essential for a comprehensive grasp of quantum entanglement. Here, in terms of the αth power of UE, we provide a new class of tighter monogamy relations for n-qudit GW states. We need the lemma below.
[Lemma 5]. For any real numbers x ≥ h ≥ 0, $1\leqslant p\leqslant 1+\tfrac{1}{x}$ and m ≥ 1, we have
$\begin{eqnarray}{\left(1+x\right)}^{m}-{p}^{m-1}{x}^{m}\geqslant {\left(1+h\right)}^{m}-{p}^{m-1}{h}^{m}.\end{eqnarray}$
Consider the function $f(x,m)={\left(1+x\right)}^{m}-{p}^{m-1}{x}^{m}$ with $x\geqslant 0$, $1\leqslant p\leqslant 1+\tfrac{1}{x}$ and $m\geqslant 1$. Since $\tfrac{\partial f(x,m)}{\partial x}$ = $m{\left(1+x\right)}^{m-1}-{{mp}}^{m-1}{x}^{m-1}$ = $m[{\left(1+x\right)}^{m-1}-{\left({px}\right)}^{m-1}]\geqslant 0$, the function $f(x,m)$ increases with x. As $x\geqslant h\geqslant 0$, we have $f{(x,m)\geqslant f(h,m)=(1+h)}^{m}-{p}^{m-1}{h}^{m}$. Therefore, we get the inequality (
For any tripartite state ${\rho }_{{P}_{1}{P}_{2}{P}_{3}}$, from (22 ) we have ${U}_{q,s}^{2}({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\geqslant {U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})+{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})$. Therefore, there exists μ ≥ 1 such that24 ) for the αth power of UE.
$\begin{eqnarray}{U}_{q,s}^{2}({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\geqslant {U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})+\mu {U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}}).\end{eqnarray}$
By using lemma 5 we improve the monogamy inequality ([Theorem 4]. Let μ ≥ 1 and h ≥ 1 be any real numbers. Let ${\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ be the reduced density matrix of an n-qudit GW state ${\left|\psi \right\rangle }_{{A}_{1}\cdots {A}_{n}}$ and {P1, P2, P3} a partition of $\{{A}_{{j}_{1}},{A}_{{j}_{2}},\cdots ,{A}_{{j}_{m}}\},$ 3 ≤ m ≤ n. If ${U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})\geqslant {{hU}}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})$ and $1\leqslant p\leqslant 1+\tfrac{\mu {U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})}{{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})}$, we have
$\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\\ \geqslant \,{p}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})+({\left(\mu +h\right)}^{\displaystyle \frac{\alpha }{2}}-{p}^{\tfrac{\alpha }{2}-1}{h}^{\displaystyle \frac{\alpha }{2}}){U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}}),\end{array}\end{eqnarray}$
with $(q,s)\in { \mathcal R }$ and α ≥ 2.By straightforward calculation, we have
$\begin{eqnarray*}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\\ \quad =\,{\left({U}_{q,s}^{2}({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\right)}^{\tfrac{\alpha }{2}}\\ \quad \geqslant {\left({U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})+\mu {U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})\right)}^{\tfrac{\alpha }{2}}\\ \quad =\,{\mu }^{\displaystyle \frac{\alpha }{2}}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}}){\left(1+\displaystyle \frac{{U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{2}})}{\mu {U}_{q,s}^{2}({\rho }_{{P}_{1}{P}_{3}})}\right)}^{\tfrac{\alpha }{2}}\\ \quad \,\geqslant {\mu }^{\displaystyle \frac{\alpha }{2}}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}})\\ \quad \times \,(\displaystyle \frac{{p}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})}{{\mu }^{\tfrac{\alpha }{2}}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}})}+{\left(1+\displaystyle \frac{h}{\mu }\right)}^{\tfrac{\alpha }{2}}-{p}^{\tfrac{\alpha }{2}-1}{\left(\displaystyle \frac{h}{\mu }\right)}^{\tfrac{\alpha }{2}})\\ \quad =\,{p}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})+({\left(\mu +h\right)}^{\displaystyle \frac{\alpha }{2}}-{p}^{\tfrac{\alpha }{2}-1}{h}^{\displaystyle \frac{\alpha }{2}}){U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}}),\end{array}\end{eqnarray*}$
where the first inequality is due to ([Remark 1]. In [34], the authors provide the following monogamy relation for an n-qudit GW state based on UE,29 ) in [34] is just a special case of our theorem 3. Moreover, it can be seen that our lower bound of the αth power of UE becomes tighter when p increases,28 ) is tighter than the result (29 ) given in [34], see the example below.
$\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\\ \quad \geqslant \,{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})+({\left(\mu +h\right)}^{\displaystyle \frac{\alpha }{\gamma }}-{h}^{\displaystyle \frac{\alpha }{\gamma }}){U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}}),\end{array}\end{eqnarray}$
for α ≥ γ, γ ≥ 1, μ ≥ 1 and h ≥ 1, with q ≥ 2, 0 ≤ s ≤ 1 and qs ≤ 3. When p = 1 and γ = 2, it is obvious that inequality ( $\begin{eqnarray*}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\\ \quad \geqslant \,{p}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})+({\left(\mu +h\right)}^{\displaystyle \frac{\alpha }{2}}-{p}^{\tfrac{\alpha }{2}-1}{h}^{\displaystyle \frac{\alpha }{2}}){U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}})\\ \quad \geqslant \,{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{2}})+({\left(\mu +h\right)}^{\displaystyle \frac{\alpha }{2}}-{h}^{\displaystyle \frac{\alpha }{2}}){U}_{q,s}^{\alpha }({\rho }_{{P}_{1}{P}_{3}}),\end{array}\end{eqnarray*}$
for all α ≥ 2, q ≥ 2, 0 ≤ s ≤ 1 and qs ≤ 3, where the second equality holds when p = 1. Hence our result ([Example 1]. Consider the following 4-qubit generalized W-class state,28 ) in theorem 4, and29 ) given in [34]. Set μ = 4 and h = 1. Figure 1 shows that (31 ) is tighter than (32 ).
$\begin{eqnarray}\begin{array}{l}{\left|\psi \right\rangle }_{{A}_{1}{A}_{2}{A}_{3}{A}_{4}}\\ =\,0.3\left|0001\right\rangle +0.4\left|0010\right\rangle +0.5\left|0100\right\rangle +\sqrt{0.5}\left|1000\right\rangle .\end{array}\end{eqnarray}$
We choose ${\rho }_{{A}_{1}{A}_{2}{A}_{3}}$ to be the reduced density matrix of ${\left|\psi \right\rangle }_{{A}_{1}{A}_{2}{A}_{3}{A}_{4}}$, P1 = A1, P2 = A2, P3 = A3. Then we have ${\rho }_{{A}_{1}{A}_{2}{A}_{3}}=0.09\left|000\right\rangle \left\langle 000\right|+\left|\phi \right\rangle \left\langle \phi \right|$, where $\left|\phi \right\rangle =0.4\left|001\right\rangle \,+0.5\left|010\right\rangle +\sqrt{0.5}\left|100\right\rangle $. By direct calculation, we get $C({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})=\sqrt{\tfrac{41}{50}}$, $C({\rho }_{{P}_{1}{P}_{2}})=\tfrac{\sqrt{2}}{2}$, $C({\rho }_{{P}_{1}{P}_{3}})=\tfrac{2\sqrt{2}}{5}$. Set γ = 2, s = 2 and q = 1. We obtain ${U}_{\mathrm{2,1}}({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})=\tfrac{41}{100}$, ${U}_{\mathrm{2,1}}({\rho }_{{P}_{1}{P}_{2}})=\tfrac{1}{4}$ and ${U}_{\mathrm{2,1}}({\rho }_{{P}_{1}{P}_{3}})=\tfrac{4}{25}$. Then we can get $\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\\ \geqslant \,{p}^{\tfrac{\alpha }{2}-1}{\left(\displaystyle \frac{1}{4}\right)}^{\alpha }+({\left(\mu +h\right)}^{\displaystyle \frac{\alpha }{2}}-{p}^{\tfrac{\alpha }{2}-1}{h}^{\displaystyle \frac{\alpha }{2}}){\left(\displaystyle \frac{4}{25}\right)}^{\alpha },\end{array}\end{eqnarray}$
from our result ( $\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})\\ \geqslant \,{\left(\displaystyle \frac{1}{4}\right)}^{\alpha }+({\left(\mu +h\right)}^{\displaystyle \frac{\alpha }{2}}-{h}^{\displaystyle \frac{\alpha }{2}}){\left(\displaystyle \frac{4}{25}\right)}^{\alpha },\end{array}\end{eqnarray}$
from the result (
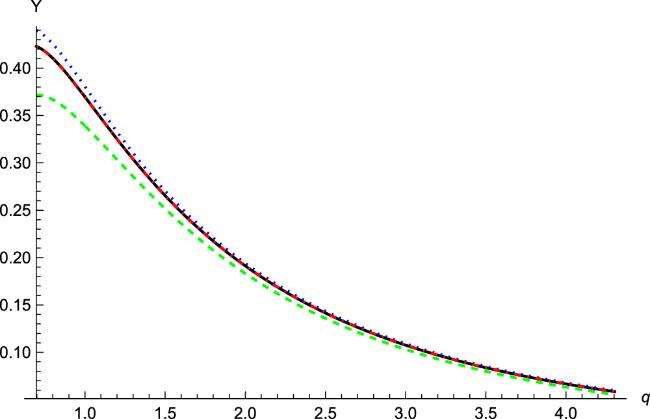
Figure 1. From top to bottom, the black line is the exact values of ${U}_{\mathrm{2,1}}({\rho }_{{P}_{1}| {P}_{2}{P}_{3}})$. The green dashed line (red dot-dashed line) represents the lower bound from our result ( |
Note that the third system P3 in theorem 3 can be divided into two subsystems. Consequently, by iterately using theorem 4 we can extend the monogamy inequality to multipartite qudit systems.
[Theorem 5]. Let μt ≥ 1 and ht ≥ 1 be real numbers, 1 ≤ t ≤ r − 2. Let ${\rho }_{{A}_{{j}_{1}}{A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}$ be the reduced density matrix of an n-qudit GW state ${\left|\psi \right\rangle }_{{A}_{1}\cdots {A}_{n}}$ and {A, B1, ⋯ ,Br−1} a partition of $\{{A}_{{j}_{1}},{A}_{{j}_{2}},\cdots ,{A}_{{j}_{m}}\},$ r ≤ m ≤ n. If ${U}_{q,s}^{2}({\rho }_{{{AB}}_{i}})\geqslant {h}_{i}{U}_{q,s}^{2}({\rho }_{A| {B}_{i+1}\cdots {B}_{r-1}})$, ${U}_{q,s}^{2}({\rho }_{A| {B}_{i}\cdots {B}_{r-1}})\,\geqslant {U}_{q,s}^{2}({\rho }_{{{AB}}_{i}})+{\mu }_{i}{U}_{q,s}^{2}({\rho }_{A| {B}_{i+1}\cdots {B}_{r-1}})$, $1\leqslant {p}_{i}\leqslant 1+\tfrac{{\mu }_{i}{U}_{q,s}^{2}({\rho }_{A| {B}_{i+1}\cdots {B}_{r-1}})}{{U}_{q,s}^{2}({\rho }_{{{AB}}_{i}})}$ for i = 1, 2, ⋯ ,k, and ${U}_{q,s}^{2}({\rho }_{A| {B}_{j+1}\cdots {B}_{r-1}})\geqslant {h}_{j}{U}_{q,s}^{2}({\rho }_{{{AB}}_{j}})$, ${U}_{q,s}^{2}({\rho }_{A| {B}_{j}\cdots {B}_{r-1}})\geqslant {\mu }_{j}{U}_{q,s}^{2}({\rho }_{{{AB}}_{j}})+{U}_{q,s}^{2}({\rho }_{A| {B}_{j+1}\cdots {B}_{r-1}})$, $1\leqslant {p}_{j}\,\leqslant \tfrac{{\mu }_{j}{U}_{q,s}^{2}({\rho }_{{{AB}}_{j}})}{{U}_{q,s}^{2}({\rho }_{A| {B}_{j+1}\cdots {B}_{r-1}})}$ for j = k + 1, ⋯ ,r − 2, 1 ≤ k ≤ r − 3 and r ≥ 4, then the UE satisfies
$\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{{P}_{1}| {P}_{2}\cdots {P}_{r}})\\ \geqslant \,{p}_{1}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{1}})+\displaystyle \sum _{i=2}^{k}\displaystyle \prod _{l=1}^{i-1}{{\rm{\Gamma }}}_{l}{p}_{i}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{i}})\\ +\,{{\rm{\Gamma }}}_{1}\cdots {{\rm{\Gamma }}}_{k+1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{k+1}})\\ +\,{{\rm{\Gamma }}}_{1}\cdots {{\rm{\Gamma }}}_{k}\displaystyle \sum _{j=k+2}^{r-2}\displaystyle \prod _{l=k+1}^{j-1}{p}_{l}^{\tfrac{\alpha }{2}-1}{{\rm{\Gamma }}}_{j}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{j}})\\ +\,{{\rm{\Gamma }}}_{1}\cdots {{\rm{\Gamma }}}_{k}{\left({p}_{k+1}\cdots {p}_{r-2}\right)}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{r-1}}),\end{array}\end{eqnarray}$
for all α ≥ 2, where ${{\rm{\Gamma }}}_{t}={({\mu }_{t}+{h}_{t})}^{\tfrac{\alpha }{2}}-{p}_{t}^{\tfrac{\alpha }{2}-1}{h}_{t}^{\tfrac{\alpha }{2}}$ with $(q,s)\in { \mathcal R }$.From theorem 4, ${U}_{q,s}^{2}({\rho }_{{{AB}}_{i}})\geqslant {h}_{i}{U}_{q,s}^{2}({\rho }_{A| {B}_{i+1}\cdots {B}_{r-1}})$, ${U}_{q,s}^{2}({\rho }_{A| {B}_{i}\cdots {B}_{r-1}})\geqslant {U}_{q,s}^{2}({\rho }_{{{AB}}_{i}})+{\mu }_{i}{U}_{q,s}^{2}({\rho }_{A| {B}_{i+1}\cdots {B}_{r-1}})$, $1\leqslant {p}_{i}\leqslant 1+\tfrac{{\mu }_{i}{U}_{q,s}^{2}({\rho }_{A| {B}_{i+1}\cdots {B}_{r-1}})}{{U}_{q,s}^{2}({\rho }_{{{AB}}_{i}})}$ for $i=1,2,\cdots ,k$. We have
$\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{A| {B}_{1}\cdots {B}_{r-1}})\\ \geqslant {p}_{1}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{1}})+{{\rm{\Gamma }}}_{1}{U}_{q,s}^{\alpha }({\rho }_{A| {B}_{2}\cdots {B}_{r-1}})\\ \geqslant {p}_{1}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{1}})+{{\rm{\Gamma }}}_{1}{p}_{2}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{2}})\\ \quad +{{\rm{\Gamma }}}_{1}{{\rm{\Gamma }}}_{2}{U}_{q,s}^{\alpha }({\rho }_{A| {B}_{3}\cdots {B}_{r-1}})\\ \geqslant \cdots \\ \geqslant {p}_{1}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{1}})+{{\rm{\Gamma }}}_{1}{p}_{2}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{2}})\\ \quad +\cdots +{{\rm{\Gamma }}}_{1}\cdots {{\rm{\Gamma }}}_{k-1}{p}_{k}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{k}})\\ \quad +{{\rm{\Gamma }}}_{1}\cdots {{\rm{\Gamma }}}_{k}{U}_{q,s}^{\alpha }({\rho }_{A| {B}_{k+1}\cdots {B}_{r-1}}).\end{array}\end{eqnarray}$
If ${U}_{q,s}^{2}({\rho }_{A| {B}_{j+1}\cdots {B}_{r-1}})\geqslant {h}_{j}{U}_{q,s}^{2}({\rho }_{{{AB}}_{j}})$, ${U}_{q,s}^{2}({\rho }_{A| {B}_{j}\cdots {B}_{r-1}})\geqslant {\mu }_{j}{U}_{q,s}^{2}({\rho }_{{{AB}}_{j}})\,+{U}_{q,s}^{2}({\rho }_{A| {B}_{j+1}\cdots {B}_{r-1}})$, $1\leqslant {p}_{j}\leqslant \tfrac{{\mu }_{j}{U}_{q,s}^{2}({\rho }_{{{AB}}_{j}})}{{U}_{q,s}^{2}({\rho }_{A| {B}_{j+1}\cdots {B}_{r-1}})}$ for $j=k+1,\cdots ,r-2$, we get $\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\alpha }({\rho }_{A| {B}_{k+1}\cdots {B}_{r-1}})\\ \geqslant {{\rm{\Gamma }}}_{k+1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{k+1}})+{p}_{k+1}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{A| {B}_{k+2}\cdots {B}_{r-1}})\\ \geqslant {{\rm{\Gamma }}}_{k+1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{k+1}})+{p}_{k+1}^{\tfrac{\alpha }{2}-1}{{\rm{\Gamma }}}_{k+2}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{k+2}})\\ \quad +{\left({p}_{k+1}{p}_{k+2}\right)}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{A| {B}_{k+3}\cdots {B}_{r-1}})\\ \geqslant \,\cdots \\ \geqslant \,{{\rm{\Gamma }}}_{k+1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{k+1}})+{p}_{k+1}^{\tfrac{\alpha }{2}-1}{{\rm{\Gamma }}}_{k+2}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{k+2}})\\ \quad +\cdots +\,{\left({p}_{k+1}\cdots {p}_{r-3}\right)}^{\tfrac{\alpha }{2}-1}{{\rm{\Gamma }}}_{r-2}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{r-2}})\\ \quad +{\left({p}_{k+1}\cdots {p}_{r-2}\right)}^{\tfrac{\alpha }{2}-1}{U}_{q,s}^{\alpha }({\rho }_{{{AB}}_{r-1}}).\end{array}\end{eqnarray}$
Combining (5. Generalized monogamy relation and upper bound for n-qudit systems
In this section, for n-qudit systems ABC1...Cn−2, we consider the generalized monogamy relation and upper bound satisfied by the βth (0 ≤ β ≤ 1) power of UE of an n-qudit GW state under the partition AB and C1...CN−2. Before showing the results, we need the following lemmas.
[Lemma 7]. [42] The function fq,s(x) given in equation (11 ) satisfies ${f}_{q,s}(\sqrt{{x}^{2}+{y}^{2}})={f}_{q,s}(x)+{f}_{q,s}(y)$ for q = 2 and $\tfrac{1}{2}\leqslant s\leqslant 1$.
[Lemma 8]. [34] Let ${\rho }_{{A}_{{j}_{1}}\cdots {A}_{{j}_{m}}}$ be a reduced density matrix of an n-qudit GW state (14 ). Then ${U}_{q,s}({\rho }_{{A}_{{j}_{1}}| {A}_{{j}_{2}}\cdots {A}_{{j}_{m}}})={f}_{q,s}(C({\rho }_{{A}_{{j}_{1}}| {A}_{{j}_{2}}\cdots {A}_{{j}_{m}}}))$ with q ≥ 1, 0 ≤ s ≤ 1 and qs ≤ 3.
[Theorem 6]. For an n-qudit GW state ${\left|\psi \right\rangle }_{{{ABC}}_{1}{C}_{2}\cdots {C}_{n-2}}$, the following inequality holds:
$\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\beta }(| \psi {\rangle }_{{AB}| {C}_{1}{C}_{2}\cdots {C}_{n-2}})\\ \geqslant \,\left|{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{AC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta }\right.\\ \left.-{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{BC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta }\right|,\end{array}\end{eqnarray}$
where q = 2 and $\tfrac{1}{2}\leqslant s\leqslant 1$.For q = 2 and $\tfrac{1}{2}\leqslant s\leqslant 1$ we have
$\begin{eqnarray}\begin{array}{l}{U}_{q,s}(| \psi {\rangle }_{A| {{BC}}_{1}{C}_{2}\cdots {C}_{n-2}})\\ =\,{f}_{q,s}(C(| \psi {\rangle }_{A| {{BC}}_{1}{C}_{2}\cdots {C}_{n-2}}))\\ =\,{f}_{q,s}(\sqrt{{C}^{2}({\rho }_{{AB}})+{C}^{2}({\rho }_{{{AC}}_{1}})+\cdots +{C}^{2}({\rho }_{{{AC}}_{n-2}})})\\ =\,\displaystyle \sum _{i=1}^{n-2}{f}_{q,s}(C({\rho }_{{{AC}}_{i}}))+{f}_{q,s}(C({\rho }_{{AB}}))\\ =\,\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{AC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}})),\end{array}\end{eqnarray}$
where the first and fourth equalities are due to lemma 8, the second and third equalities are due to lemma 4 and lemma 7, respectively. Similarly, we have $\begin{eqnarray}\begin{array}{l}{U}_{q,s}(| \psi {\rangle }_{B| {{AC}}_{1}{C}_{2}\cdots {C}_{n-2}})\\ =\,\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{BC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}})).\end{array}\end{eqnarray}$
From the subadditivity of the unified-($q,s$) entropy for a quantum state ${\rho }_{{AB}}$ [43], $| {U}_{q,s}({\rho }_{A})-{U}_{q,s}({\rho }_{B})| \leqslant {U}_{q,s}({\rho }_{{AB}})\leqslant {U}_{q,s}({\rho }_{A})+{U}_{q,s}({\rho }_{B})$, we have $\begin{eqnarray*}\begin{array}{l}{U}_{q,s}^{\beta }(| \psi {\rangle }_{{AB}| {C}_{1}{C}_{2}\cdots {C}_{n-2}})={U}_{q,s}^{\beta }({\rho }_{{AB}})\\ \geqslant \,| {U}_{q,s}({\rho }_{A})-{U}_{q,s}({\rho }_{B}){| }^{\beta }\\ \geqslant \,| {U}_{q,s}^{\beta }({\rho }_{A})-{U}_{q,s}^{\beta }({\rho }_{B})| \\ =\,\left|{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{AC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta }\right.\\ \left.-{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{BC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta }\right|,\end{array}\end{eqnarray*}$
where the second inequality is due to the subadditivity of UE, the third inequality is by lemma 6, the last equality is obtained from equations ([Remark 2]. In [34], the authors give the following generalized monogamy relation,
$\begin{eqnarray*}\begin{array}{l}{U}_{q,s}(| \psi {\rangle }_{{AB}| {C}_{1}{C}_{2}\cdots {C}_{n-2}})\\ \geqslant \,\left|\displaystyle \sum _{i=1}^{n-2}[{U}_{q,s}(C({\rho }_{{{AC}}_{i}}))-{U}_{q,s}(C({\rho }_{{{BC}}_{i}})]\right|,\end{array}\end{eqnarray*}$
which is obviously a special case of our theorem 6 when β = 1. Moreover, when β = 1 and s = 1, theorem 5 reduces to the generalized monogamy relation in terms of the Tsallis-2 entanglement given in [32].According to the subadditivity of the unified-(q, s) entropy, we also have the following upper bound of UE.
[Theorem 7]. For an n-qudit GW state ${\left|\psi \right\rangle }_{{{ABC}}_{1}{C}_{2}\cdots {C}_{n-2}}$, the following inequality holds,
$\begin{eqnarray}\begin{array}{l}{U}_{q,s}^{\beta }(| \psi {\rangle }_{{AB}| {C}_{1}{C}_{2}\cdots {C}_{n-2}})\\ \leqslant \,{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{AC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta }\\ \quad +\,{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{BC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta },\end{array}\end{eqnarray}$
where q = 2 and $\tfrac{1}{2}\leqslant s\leqslant 1$.Using the subadditivity of unified-($q,s$) entropy, we have the following inequality,
$\begin{eqnarray*}\begin{array}{l}{U}_{q,s}^{\beta }(| \psi {\rangle }_{{AB}| {C}_{1}{C}_{2}\cdots {C}_{n-2}})={U}_{q,s}^{\beta }({\rho }_{{AB}})\\ \leqslant \,({U}_{q,s}({\rho }_{A})+{U}_{q,s}{\left({\rho }_{B})\right)}^{\beta }\\ \leqslant \,{U}_{q,s}^{\beta }({\rho }_{A})+{U}_{q,s}^{\beta }({\rho }_{B})\\ =\,{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{AC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta }\\ +\,{\left(\displaystyle \sum _{i=1}^{n-2}{U}_{q,s}(C({\rho }_{{{BC}}_{i}}))+{U}_{q,s}(C({\rho }_{{AB}}))\right)}^{\beta },\end{array}\end{eqnarray*}$
where the second inequality is due to the subadditivity of UE, the third inequality is by lemma 6, the last equality is obtained by using equations (6. Applications
To investigate the entanglement properties of multi-qubit W-class states, in this section we first present two monogamy-like inequalities of PREs for GW states by utilizing theorem 2. For an n-qubit GW state ${\left|\varphi \right\rangle }_{{A}_{1}{A}_{2}\cdots {A}_{n}}$, we can always divide the whole system into two subsystems under any partition P = {P1, P2} of {A1, ⋯ ,An}, such that P1 = {A1, A2, ⋯ ,Am} and P2 = {Am+1, Am+2, ⋯ ,An}. Each subsystem can be further partitioned as P1 = {P11, P12} and P2 = {P21, P22}, where P11 = {A1, ⋯ ,Aa}, P12 = {Aa, ⋯ ,Am} and P21 = {Am+1, ⋯ ,Ab}, P22 = {Ab+1, ⋯ ,An}. Since the partition P = {P1, P2, ⋯ ,Pr} in theorem 2 is arbitrary, if we take r = 3 and P = {P11P12, P21, P22}, according to the monogamy relation in theorem 2 we obtain
$\begin{eqnarray}\begin{array}{rcl} & & {U}_{q,s}^{2}({\rho }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}})\\ & \geqslant & {U}_{q,s}^{2}({\rho }_{{P}_{11}{P}_{12}| {P}_{21}})+{U}_{q,s}^{2}({\rho }_{{P}_{11}{P}_{12}| {P}_{22}})\\ & \geqslant & {U}_{q,s}^{2}({\rho }_{{P}_{11}| {P}_{21}})+{U}_{q,s}^{2}({\rho }_{{P}_{12}| {P}_{21}})\\ & & +\,{U}_{q,s}^{2}({\rho }_{{P}_{11}| {P}_{22}})+{U}_{q,s}^{2}({\rho }_{{P}_{12}| {P}_{22}})\\ & \geqslant & \displaystyle \sum _{i=1}^{m}\displaystyle \sum _{j=m+1}^{n}{U}_{q,s}^{2}({\rho }_{{A}_{i}{A}_{j}}),\end{array}\end{eqnarray}$
by repeatedly applying the second inequality. Clearly, the above inequality relations hold for any partition given by a, m and b with 1 ≤ a ≤ m < b ≤ n.From inequality (40 ), we have the following PREs in terms of the unified-(q, s) entanglement,
$\begin{eqnarray}\begin{array}{rcl}{{\rm{\Upsilon }}}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}} & = & {U}_{q,s}^{2}({\rho }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}})-{U}_{q,s}^{2}({\rho }_{{P}_{11}| {P}_{21}})\\ & & -{U}_{q,s}^{2}({\rho }_{{P}_{12}| {P}_{21}})-{U}_{q,s}^{2}({\rho }_{{P}_{11}| {P}_{22}})\\ & & -{U}_{q,s}^{2}({\rho }_{{P}_{12}| {P}_{22}}),\end{array}\end{eqnarray}$
and $\begin{eqnarray}\begin{array}{rcl}{\rm{\Upsilon }}{{\prime} }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}} & = & {U}_{q,s}^{2}({\rho }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}})\\ & & -\displaystyle \sum _{i=1}^{m}\displaystyle \sum _{j=m+1}^{n}{U}_{q,s}^{2}({\rho }_{{A}_{i}{A}_{j}}).\end{array}\end{eqnarray}$
The monogamy inequality (40 ) and the PREs (41 ) and (42 ) contain all possible bipartitions for n-qubit systems. The PRE captures entanglement properties under arbitrary partitions, elucidating various multi-partitioned entanglements with respect to a, m and b. Let us take the n-qubit W state ${\left|W\right\rangle }_{{A}_{1}{A}_{2}\cdots {A}_{n}}$ to illustrate our inequalities and PREs,
$\begin{eqnarray*}{\left|W\right\rangle }_{{A}_{1}{A}_{2}\cdots {A}_{n}}=\displaystyle \frac{1}{\sqrt{N}}(| 10\cdots 0\rangle +| 01\cdots 0\rangle +| 0\cdots 01\rangle ).\end{eqnarray*}$
For $(q,s)\in { \mathcal R }$, using theorem 1 we obtain $\begin{eqnarray}\begin{array}{rcl}{{\rm{\Upsilon }}}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}} & = & {g}_{q,s}^{2}({C}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}})-{g}_{q,s}^{2}({C}_{{P}_{11}| {P}_{21}})\\ & & -{g}_{q,s}^{2}({C}_{{P}_{12}| {P}_{21}})-{g}_{q,s}^{2}({C}_{{P}_{11}| {P}_{22}})\\ & & -{g}_{q,s}^{2}({C}_{{P}_{12}| {P}_{22}}),\end{array}\end{eqnarray}$
and $\begin{eqnarray}\begin{array}{rcl}{\rm{\Upsilon }}{{\prime} }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}} & = & {g}_{q,s}^{2}({C}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}})\\ & & -\displaystyle \sum _{i=1}^{m}\displaystyle \sum _{j=m+1}^{n}{g}_{q,s}^{2}({C}_{{A}_{i}{A}_{j}}).\end{array}\end{eqnarray}$
By direct calculation we have ${C}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}^{2}=\tfrac{4m(n-m)}{{n}^{2}}$, ${C}_{{P}_{11}{P}_{21}}^{2}=\tfrac{1}{{n}^{2}}{[\sqrt{{(n-m)}^{2}+4a(b-m)}-(n-m)]}^{2}$, ${C}_{{P}_{12}{P}_{21}}^{2}=\tfrac{1}{{n}^{2}}{[\sqrt{{(n-m)}^{2}+4(m-a)(b-m)}-(n-m)]}^{2}$, ${C}_{{P}_{11}{P}_{22}}^{2}=\tfrac{1}{{n}^{2}}{[\sqrt{{(n-m)}^{2}+4a(n-b)}-(n-m)]}^{2}$, ${C}_{{P}_{12}{P}_{22}}^{2}=\tfrac{1}{{n}^{2}}{[\sqrt{{(n-m)}^{2}+4(m-a)(n-b)}-(n-m)]}^{2}$ and ${C}_{{A}_{i}{A}_{j}}^{2}=\tfrac{1}{{n}^{2}}{[\sqrt{4+{(n-2)}^{2}}-(n-2)]}^{2}$ [33, 38].When s tends to 1, the unified-(q, s) entropy converges to Tsallis-q entropy. In this case the PRE ${{\rm{\Upsilon }}}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ (41 ) relies on the two partitions in terms of a, m and b. Let n = 6 and m = 4. Then a can be 1, 2, 3 and 4, and b be 5 or 6. For all the possible values of a and b the value of the PRE ${{\rm{\Upsilon }}}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ for a 6-qubit W-class state is shown in tables 1 and 2.
Table 1. The values of PRE ${{\rm{\Upsilon }}}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ for different q and all the possible values of a, denoted by ϒ(q, a, b), when s = 1, m = 4, b = 5, n = 6. |
| q | ϒ(q, 1, 5) | ϒ(q, 2, 5) | ϒ(q, 3, 5) | ϒ(q, 4, 5) |
|---|---|---|---|---|
| 2.0 | 0.191 172 | 0.193 981 | 0.191 172 | 0.183 117 |
| | ||||
| 2.1 | 0.179 591 | 0.182 176 | 0.179 591 | 0.172876 |
| | ||||
| 2.2 | 0.168 899 | 0.171 295 | 0.168 899 | 0.162006 |
| | ||||
| 2.3 | 0.159 022 | 0.161 259 | 0.159 022 | 0.152585 |
| | ||||
| 2.4 | 0.149 893 | 0.151 993 | 0.149 893 | 0.143847 |
Table 2. The values of PRE ${{\rm{\Upsilon }}}_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ for different q and all the possible values of a, denoted by ϒ(q, a, b), when s = 1, m = 4, b = 6, n = 6. |
| q | ϒ(q, 1, 6) | ϒ(q, 2, 6) | ϒ(q, 3, 6) | ϒ(q, 4, 6) |
|---|---|---|---|---|
| 2.0 | 0.173 999 | 0.183 117 | 0.173 999 | 0.148 145 |
| | ||||
| 2.1 | 0.163 680 | 0.172 876 | 0.163 680 | 0.139568 |
| | ||||
| 2.2 | 0.154 082 | 0.162 006 | 0.154 082 | 0.131526 |
| | ||||
| 2.3 | 0.145 158 | 0.152 585 | 0.145 158 | 0.123996 |
| | ||||
| 2.4 | 0.136 863 | 0.143 847 | 0.136 863 | 0.116952 |
We observe that the values in table 1 with b = 5 are greater than those in table 2 with b = 6, and the values of ϒ(q, 4, 5) and ϒ(q, 2, 6) are equal. In table 1 (table 2), the PRE has the same value when a = 1 and a = 3, and the PRE gets the maximum value when a = 2 and the minimum when a = 4. If a, m, b are fixed for $\tfrac{5-\sqrt{13}}{2}\leqslant q\leqslant \tfrac{5+\sqrt{13}}{2}$, the value of PRE decreases with the increase of q, as shown in figure 2 and figure 3, corresponding to tables 1 and 2, respectively.
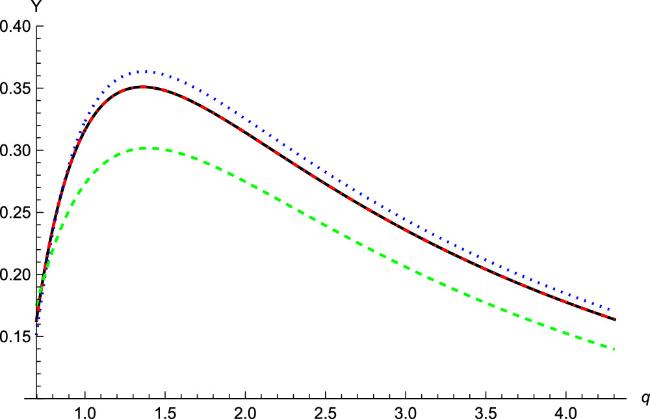
Figure 2. s = 1, m = 4, b = 5, n = 6. From top to bottom, the blue dotted line represents a = 2, the black line represents a = 1, the red dot-dashed line represents a = 3, and the green dashed line represents a = 4. The curves coincide when a = 1 and a = 3. |
Figure 3. s = 1, m = 4, b = 6, n = 6. From top to bottom, the blue dotted line represents a = 2, the black line represents a = 1, the red dot-dashed line represents a = 3, and the green dashed line represents a = 4. The curves coincide when a = 1 and a = 3. |
On the other hand, the PRE ${\rm{\Upsilon }}{{\prime} }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ in equation (42 ) is only related to the first partition in terms of m. Set n = 6. Then, the value of m can be 1, 2, 3, 4, 5. The values of PRE ${\rm{\Upsilon }}{{\prime} }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ are shown in table 3 when s = 1.
Table 3. The values of PRE ${\rm{\Upsilon }}{{\prime} }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ for different q and all the possible values of m, denoted by ${\rm{\Upsilon }}^{\prime} (q,m)$, when s = 1 and n = 6. |
| q | ${\rm{\Upsilon }}^{\prime} (q,1)$ | ${\rm{\Upsilon }}^{\prime} (q,2)$ | ${\rm{\Upsilon }}^{\prime} (q,3)$ | ${\rm{\Upsilon }}^{\prime} (q,4)$ | ${\rm{\Upsilon }}^{\prime} (q,5)$ |
|---|---|---|---|---|---|
| 2.0 | 0.077 113 | 0.197 450 | 0.249 914 | 0.197 450 | 0.077113 |
| | |||||
| 2.1 | 0.071 820 | 0.185 350 | 0.235 131 | 0.185350 | 0.071820 |
| | |||||
| 2.2 | 0.067 131 | 0.174 229 | 0.221 395 | 0.174229 | 0.067131 |
| | |||||
| 2.3 | 0.062 961 | 0.163 993 | 0.208 622 | 0.163993 | 0.062961 |
| | |||||
| 2.4 | 0.059 234 | 0.154 560 | 0.196 737 | 0.154560 | 0.059234 |
We see that the value of PRE ${\rm{\Upsilon }}{{\prime} }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ is the same when m = 1 (m = 2) and m = 5 (m = 4), and the value is maximum when m = 3. The above results are also due to the structural particularity of the W-class state. If m and n are fixed for $\tfrac{5-\sqrt{13}}{2}\leqslant q\leqslant \tfrac{5+\sqrt{13}}{2}$, the value of PRE ${\rm{\Upsilon }}{{\prime} }_{{P}_{11}{P}_{12}| {P}_{21}{P}_{22}}$ decreases with the increase of q, as shown in figure 4, corresponding to the case in table 3. These results of PREs show the entanglement structures of the six-qubit W state.
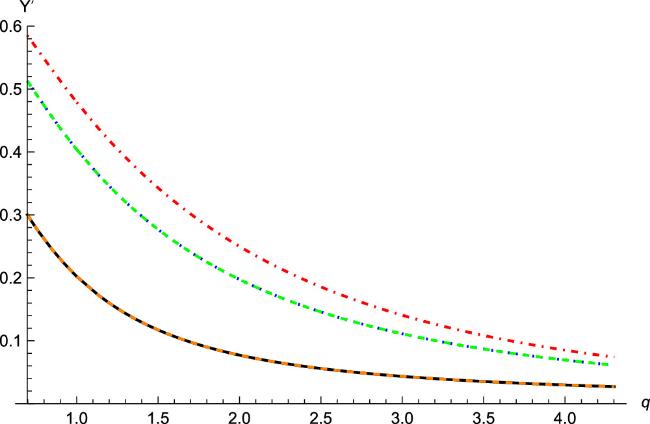
Figure 4. s = 1, n = 6. From top to bottom, the red dot-dashed line represents m = 3, the blue dotted line represents m = 2, the green dashed line represents m = 4, the black line represents m = 1, and the orange dashed line represents m = 5. The curves coincide when m = 1 (m = 2) and m = 5 (m = 4). |
7. Conclusion
The monogamy relations of quantum entanglement are the essential characteristics displayed by multiqudit entangled states. We have investigated monogamy properties related to the unified-(q, s) entropy for n-qudit GW states under any partition. We have provided an analytical formula of the unified-(q, s) entanglement with extended (q,s) region for $(q,s)\in { \mathcal R }$. By using the analytical formula, the monogamy relation based on the squared UE for a qudit GW state has been presented. Since the distribution of entanglement in multi-qudit systems can be better understood by employing stricter monogamy inequalities, we have also investigated tighter monogamy relations based on the αth (α ≥ 2) power of the UE. Furthermore, for n-qudit systems ABC1...Cn−2, generalized monogamy relation and upper bound satisfied by the βth (0 ≤ β ≤ 1) power of UE for the GW states have been established under the partition AB and C1...Cn−2. To demonstrate the significance of our conclusions, we have presented the two partition-dependent residual entanglements to give a comprehensive analysis of the entanglement structure of the GW states. Our results indicate that the UE serves as an effective measure of entanglement in multi-qudit systems in the MoE framework. When the parameters q and s of the unified-(q, s) entanglement converge to some values, our results turn to be the ones for other entanglement measures. Our results may shed new light on further investigations on comprehending the distribution of entanglement in other multipartite systems. A proper entanglement measure should satisfy three basic conditions [44], including the monotonicity [45], namely, the measure does not increase on average under local operations and classical communication. It remains unclear whether the unified entanglement constitutes an entanglement monotone. In our future work, we hope to be able to answer this question.