1. Introduction
Recent astrophysical data obtained from a variety of sources, such as high red-shift type Ia supernovae, observations from the cosmic microwave background radiations, matter power spectra analysis, observed Hubble parameter data and the investigation of the large-scale structure of the Universe has provided compelling evidence supporting the notion that our mysterious cosmos is currently expanding at an accelerated rate [1–8]. To address these discoveries, scientists proposed the presence of a mysterious dark constituent of our Universe, i.e., dark matter (DM) and dark energy (DE) in which the latter is considered one of the contenders for the accelerated expansion of the cosmos, which fills all of space and assumed to have a negative pressure that opposes the gravitational attraction of matter and causes the expansion to accelerate. One possible explanation for DE is the cosmological constant, which Einstein introduced to explain the observed acceleration of cosmic expansion. It faces several theoretical challenges and is denoted as Λ. The most notable among these are the problems posed by its observed value with present cosmological frameworks and also due to issues stemming from having a fixed equation of state (EoS) over time.
On the other hand, DM is a hypothetical form of matter that does not interact with light or other electromagnetic radiation. It detects its gravitational effects on luminous structures and is postulated to explain various observations that cannot be detected by visible matter alone. The rotational velocities of galaxies and the motion of stars within galaxy clusters indicate the presence of an additional mass that is not detected by visible matter. The gravitational effects of this unseen mass, believed to be DM, help to explain the observed motions and dynamics of these relativistic structures. Several theoretical candidates for DM have been proposed, including weakly interacting massive particles, axions, and sterile neutrinos, among others. According to the Λ-CDM model, the Universe is believed to consist of approximately 71% DE, around 24% DM and 5% ordinary matter (the stuff that makes up stars, planets, and everything that we can see).
General Relativity (GR) is one of the best theories of individual intellect, but it has certain limitations. For example, without taking DE into account, GR is unable to account for the reported acceleration of the growth of the Universe. To address concerns about fine-tuning and exploring time-evolving dynamics more thoroughly, other approaches may be explored. Consequently, in order to account for some scientific findings and cosmic mysteries, adjustments to GR are required [9–23]. One approach to addressing the mysterious nature of these hypothetical components of our Universe is to explore modified theories of gravity. These theories go beyond Einstein’s GR and introduce modifications to the gravitational equations. The goal is to account for the impacts of DE while also providing a theoretical framework to explain the observed accelerated growth. The extended gravity theories provide alternate explanations for gravity’s behavior on cosmic scales. The investigation of extended theories of gravity includes theoretical computations, numerical simulations, and comparisons with empirical facts. The scientists analyze predictions regarding these theories and put them to the test against existing data and future experiments.
The D-dimensional extension of GR is given by the Lovelock action containing several extra terms, which is named after a mathematician and physicist David Lovelock, who introduced it in 1971, in which he studied the conservation nature of second-order equation of motion in ${\mathbb{D}}$-dimensional space-time. The Lovelock action includes higher-order curvature terms in addition to the standard Einstein–Hilbert term [24]. In three and four dimensions $({\mathbb{D}}=3,4)$, Lovelock’s theory aligns with Einstein’s, but in dimensions beyond four, distinctions emerge. Consequently, it essentially serves as the natural expansion of Einstein’s GR into higher dimensions, with Einstein gravity seen as a specific case within Lovelock gravity for ${\mathbb{D}}\gt 4$. When generalized Euler density becomes a topological object, it is studied in a ${\mathbb{D}}=2n$ dimensional space-time, see [25, 26] for further details. Glavan and Lin [27] introduced $4{\mathbb{D}}$ EGB theory of gravity to discuss the propagation of massless gravitons and criteria of generic covariance in a $4{\mathbb{D}}$ space-time. This gravity contains a cosmological constant and Gauss–Bonnet (GB) term multiplied by the factor $1/({\mathbb{D}}-4)$, which helps to obtain more understanding of the dynamic behavior of relativistic structures and resolve singularities in spherically symmetric solutions in $4{\mathbb{D}}$ spacetime (for further details one may see [28–31]). Recently, Zubair and Mushayydha [32] studied bouncing cosmology under the influence of EGB gravity theory with four different models, such as (i) matter bounce, (ii) oscillatory bounce, (iii) super bounce, and (iv) symmetric bounce. They computed expressions in a general form for energy density, surface pressure, and the EoS parameter with EGB gravity theory to investigate isotropic, homogeneous, and FLRW cosmology. They also explored the physical interpretation of the Hubble and deceleration parameters for each bouncing model with the help of scale factors. The approach they used in their analysis also explores how energy criteria are violated in bouncing models. They developed analytical formulas for the jerk and snap parameters, which, concerning cosmic time and red-shift, respectively, represent the rate of acceleration change and higher derivatives of the expansion. Through certain cosmographic testing, the veracity of bouncing models is also determined. They worked for different bouncing models and their implications on energy conditions, stability, and performs parameter fitting, using observational Hubble data sets.
Recent studies have addressed theoretical challenges by rescaling the GB coupling constant, demonstrating different fluid configurations in $4{\mathbb{D}}$. Hassan and Sahoo [33] examined DM profiles and wormhole solutions in galactic halos for spherically symmetric space-time, focusing on energy conditions and the impact of the GB coefficient. However, the justification for dimensional-regularization prescriptions is still limited. Yousaf and collaborators [34] investigated how $4{\mathbb{D}}$ EGB gravity affects the inhomogeneity of initially non-uniform relativistic spheres. They analyzed kinematical variables and derived the equations of motion for a spherically symmetric, self-gravitating matter distribution. By using the Weyl tensor, they studied the evolution equations to gain insights into inhomogeneity in shear-free matter distributions, concluding that GB terms play a role in maintaining regularity in collapsing fluids. Sergey and Ekaterina [35] investigated de Sitter solutions in EGB gravity models, which are vital for understanding inflation and late-time cosmic acceleration. They discovered that stable de Sitter solutions, corresponding to the minima of effective potentials, facilitate the identification and analysis of inflationary and dark energy scenarios. The static compact hyperbolically symmetric structure studied in [36] with two unequal primary stresses and negative energy density are relevant in extreme cosmological using two generating functions. Brassel et al [37] examined the essential conditions for developing a model of a charged, anisotropic compact star in higher dimensions using a generic form of EGB gravity, considering a non-zero cosmological constant in which they found that when the star’s boundary is modeled as a time-like hypersurface of negligible thickness, the generalized matching criteria across this boundary are satisfied. Also, their study highlighted that the Darmois–Israel junction conditions are sufficient for meeting these matching requirements, facilitating the creation of a complete stellar model in considered gravity which effectively connects the star’s interior to the exterior higher-dimensional spacetime, while the effects of complexity on anisotropic charged compact structure studied in [38], in which complexity factor derived from the Riemann curvature tensor.
The static and dynamic spherical solutions in the context of some modified gravity models are investigated to study thermodynamics and the dynamical instability constraints, also the behavior of some compact fluid configurations with and without electromagnetic effects studied in [39–47], Oikonomou [48] studied the synergistic effects of f(R) theory on the gravitational waves for post-inflationary epoch with two different cases of EoS, one with EoS parameter Φ = − 1/3 and other one is Φ = 0. Mustafa et al [49] conceived a traversable wormhole in modified gravity which satisfied the energy conditions.
Bhatti et al [50, 51] studied dynamical behavior of compact structures in the scenario of modified gravities. Their findings showed that the structural coefficients and extra curvature factors appeared due to considered modified gravity theories affecting the dynamical behavior of the system. Yousaf et al [52, 53] studied and provided insights into the properties and behavior of a particular class of self-gravitating compact structure, (i.e., gravastar) with and without the influence of electromagnetic fields under the non-minimally coupled theory of gravity by considering both analytical and regular solutions.
In order to analyze self-gravitating structures employing either N or generalized relativistic models, it is essential to comprehend their behavior. Fluid spheres that are prone to dynamic instability collapse as a result of slight changes in their distribution based on gravitational pull. The strong gravitational pull produced by the fluid mass under consideration gives rise to this problem. Consequently, a self-gravitational force is the main factor that plays a vital role to control behavior of astrophysical systems, core-collapse supernovae and formations of different compact objects, like stars, galaxies, and even phenomena like solar flares or magneto-spheric sub-storms. The mass function, the density profile, and the fluid’s EoS are some of the variables that affect how spherically symmetric fluid distributions behave. Understanding of the dynamical instability of these sorts of distribution models, the formation and evolution of stars, as well as knowledge of other structures like galaxies, have all been revealed through research in the literature [54–56].
Chandrasekhar studied the dynamical stability of compact systems undergoing the collapsing phase and discussed the mass limit that leads to the formation of such systems [57]. These findings showed significant influence on astrophysics and related fields, which provided the foundations for further study to discuss the dynamics and evolution of celestial objects. Astashenok et al [58] presented modification related to the Chandrasekhar mass limit for white dwarfs under the influence of a specific form of modified gravity with simple relativistic polytropic EoS and the realistic Chandrasekhar EoS. To analyze the white dwarfs, they over-sighted the factors associated with the relativistic effects of GR. Herrera et al [59, 60] investigated the gravitational collapse and the dynamical instability of relativistic structures. They demonstrated how different relativistic systems’ stability thresholds can be from the Chandrasekhar limit by extending their research to a variety of fluid types, including ideal fluids and anisotropic fluids with dissipative effects like viscosity and heat conduction [60–63]. Herrera and his collaborators [64] delved into an idea initially advanced by Zeldovich and Novikov many years back, concerning the potential existence of compact entities characterized by extremely minute mass. This class of objects, known as ghost stars, has areas in their fluid distribution where the energy density becomes negative, resulting in an asymptotically low total mass. As a result, the interior seamlessly crosses over to Minkowski space-time at the boundary. A variety of accurate analytical solutions presented and their qualities thoroughly examined. Additionally, they debated observational evidence that may support or refute the existence of these celestial bodies. Certain behaviors of different compact objects under various backgrounds was studied in [65–74].
The adiabatic index Γ approach, which describes the relationship between pressure and density changes in fluid formations, is used to evaluate the range of the instability. It can be demonstrated that relativistic systems become unstable when Γ is less than 4/3, since this causes gravitational collapse, whereas values higher than 4/3 specify stable behavior (the system resists against collapsing scenario). Therefore, it is crucial to study how variations in Γ affect the astrophysical evolution processes involved in the birth of stars and galaxies and how they affect the evolution of cosmic systems. The findings of this study provide a notable advancement in our understanding of the behavior of fluid spheres when subjected to expansion scalar and how such conditions affect their dynamical instability [75–84]. We use a radial perturbative approach for our examination in which adiabatic parameter Γ has an impact on the dynamical instability spectrum across the N and PN approaches. A semi-numerical method, initially developed for post-quasi-static gravitational collapse, has been adjusted to bypass direct integration of underlying equations by imposing constraints on fluid distribution. Herrera et al [85] adopted the vanishing complexity factor condition, enabling analytical integration and the creation of physically meaningful models for post-quasi-static gravitational collapse. However, they studied the homologous and quasi-homologous evolutions, which proved unsuitable for post-quasi-static approximation, leading to incompatible geodesic fluids. Adiabatic evolution also results in such fluids, necessitating exclusive consideration of dissipative systems. Comprehensive model descriptions require additional information, accessible through observable quantities or heuristic mathematical assumptions. They illustrated this modified approach and studied two models inspired by the Schwarzschild interior and Tolman VI solutions showcase the practical application of the adapted methodology. Bhatti et al [83, 86], by using a radial perturbation approach, investigated the instability under modified gravity and the structural coefficients are what determine the overall dynamics of the entire structure. One may check out the whole study for more information and other references [87–90]. The article is planned to be formatted as follows.
References: A list of the sources used throughout the study is included in the body of the paper as a final section.
| 1. Introduction: This section presents the idea of fluid spheres with an expansion scalar and addresses modified gravity. It also contains prior information and emphasizes the significance of the study. | |
| 2. Mathematical framework: This section provides the fundamental mathematical foundation for the study. It contains the junction conditions, field equations, and energy-momentum tensor that serve as the study’s foundation. | |
| 3. Perturbation scheme and collapse equation: This section describes the perturbation scheme used in the analysis. We separate the static and non-static parts of modified field equations, mass functions, kinematical quantities, and conservation equations. Also, the dynamical collapse equation is derived in the same section, which helps to explain the behavior of fluid spheres. | |
| 4. Instability domains: In this section, we outline the methodology employed and examine the stability criteria for relativistic spheres at the N and PN epochs along with ${\mathbb{D}}$-dimensional modified correction terms via theoretical and pictorial representations. | |
| 5. Summary of work: The concluding part of the written work is found in this section along with some final observations on the significance and potential uses of the findings. | |
| 6. Intermediate mathematical terms (Appendix): It contains the comprehensive intermediate mathematics used in the deductions and evaluation procedures described in the text. This makes it possible for those who are interested to examine the computations while also ensuring that the technique is transparent. |
2. Mathematical framework
In the following section, we examine anisotropic symmetric fluid spheres with D-dimensional modified gravity. We also establish the modified field equations, kinematic quantities, mass function and non-zero components of the conserved equation of motion, and specific matching constraints along with ${\mathbb{D}}$-dimensional modified correction terms.
2.1. Fluid spheres, anisotropic matter tensor and some kinematic quantities
Considering ${\mathbb{D}}$-dimensions, the most general interior spherically symmetric metric can be defined as
$\begin{eqnarray}\begin{array}{rcl}{{\rm{d}}{s}}_{-}^{2} & = & -{{\mathbb{E}}}^{2}(t,r){{\rm{d}}{t}}^{2}+{{\mathbb{F}}}^{2}(t,r){{\rm{d}}{r}}^{2}+{r}^{2}\\ & & \times \,\left[{\rm{d}}{\theta }_{1}^{2}+\displaystyle \sum _{i=2}^{{\mathbb{D}}}\displaystyle \prod _{j=1}^{i-1}{\sin }^{2}{\theta }_{j}{\rm{d}}{\theta }_{i}^{2}\right]\end{array}\end{eqnarray}$
with ${\mathbb{D}}$ being the dimension and ${\theta }_{1},{\theta }_{2},\,\ldots ,\,{\theta }_{{\mathbb{D}}-1},{\theta }_{{\mathbb{D}}}$ the angular coordinates. In our considered scenario the ${\mathbb{D}}$-2 sphere is defined as a relativistic non-static fluid distribution. It is thought to have local anisotropy, and the line element inside boundary Σ(e) in terms of co-moving coordinates is supplied by: $\begin{eqnarray}{{\rm{d}}{s}}_{-}^{2}=-{{\mathbb{E}}}^{2}{{\rm{d}}{t}}^{2}+{{\mathbb{F}}}^{2}{{\rm{d}}{r}}^{2}+{{\mathbb{G}}}^{2}{\rm{d}}{{\rm{\Phi }}}_{{\mathbb{D}}-2}^{2},\end{eqnarray}$
as ${\rm{d}}{{\rm{\Phi }}}_{{\mathbb{D}}-2}^{2}={\rm{d}}{\theta }^{2}+{\sin }^{2}\theta {\rm{d}}{\phi }^{2}$, and the metric functions ${\mathbb{E}}$, ${\mathbb{F}}$, and ${\mathbb{G}}$ are functions of t and r, which are coefficients of considered metrics and assumed to be positive. The mathematical representation for matter tensor ${T}_{\aleph \upsilon }^{-}$ which is a source of an adiabatic and locally anisotropic distribution of matter and energy given as $\begin{eqnarray}{T}_{\aleph \upsilon }^{-}=\left(\mu +{{\mathbb{P}}}_{\perp }\right){V}_{\aleph }{V}_{\upsilon }+{{\mathbb{P}}}_{\perp }{g}_{\aleph \upsilon }+\left({{\mathbb{P}}}_{r}-{{\mathbb{P}}}_{\perp }\right){\chi }_{\aleph }{\chi }_{\upsilon }.\end{eqnarray}$
Here, surface pressure components in respective directions are ${{\mathbb{P}}}_{r}$, ${{\mathbb{P}}}_{\perp }$ and energy density is denoted by μ. Also, Vℵ is four-velocity and χℵ denotes unit four-vector which satisfies the relationship $\begin{eqnarray*}{V}^{\aleph }{V}_{\aleph }=-1,\quad {\chi }^{\aleph }{\chi }_{\aleph }=1,\quad {\chi }^{\aleph }{V}_{\aleph }=0.\end{eqnarray*}$
For this system, four-acceleration and expansion of fluid are $\begin{eqnarray*}{\rm{\Theta }}={V}_{;\aleph }^{\aleph },\,{a}_{\aleph }={V}_{\aleph ;\upsilon }{V}^{\upsilon }.\end{eqnarray*}$
Additionally, we may represent the shear of the fluid in tensorial form as $\begin{eqnarray*}{\sigma }_{\aleph \upsilon }={V}_{(\aleph ;\upsilon )}+{a}_{(\aleph }{V}_{\upsilon )}-\displaystyle \frac{1}{3}{\rm{\Theta }}\left({g}_{\aleph \upsilon }+{V}_{\aleph }{V}_{\upsilon }\right).\end{eqnarray*}$
We define $\begin{eqnarray*}{V}^{\aleph }={{\mathbb{E}}}^{-1}{\delta }_{0}^{\aleph },\,{\chi }^{\aleph }={{\mathbb{F}}}^{-1}{\delta }_{1}^{\aleph },\end{eqnarray*}$
and expressions for scalar values of the expansion and shear tensors of sphere-shaped distribution turn out $\begin{eqnarray}{\rm{\Theta }}=\displaystyle \frac{2}{{\mathbb{EFG}}}\left(\displaystyle \frac{\dot{{\mathbb{F}}}}{2}+\dot{{\mathbb{G}}}\right),\quad \sigma =\displaystyle \frac{1}{{\mathbb{EFG}}}\left(\dot{{\mathbb{F}}}-\dot{{\mathbb{G}}}\right).\end{eqnarray}$
2.2. Theory and modified field equations
One can find the action for ${\mathbb{D}}$-dimensional EGB gravity which includes the Gauss–Bonnet (GB) term in the introductory work of Glavan and his collaborator [27]. In $4{\mathbb{D}}$ spacetime, this factor is a topological invariant, contributing to the Euler characteristic ${\mathfrak{I}}({M}_{4})$ through the integral
$\begin{eqnarray}{\mathfrak{I}}({M}_{4})=\displaystyle \frac{1}{32}{\int }_{{M}_{4}}\displaystyle \frac{\sqrt{-g}}{{\pi }^{2}}{ \mathcal G }{{\rm{d}}}^{4}x,\end{eqnarray}$
where ${ \mathcal G }$ is the GB invariant, given by ${ \mathcal G }={R}^{\aleph \upsilon }{}_{\rho \sigma }{R}^{\rho \sigma }{}_{\aleph \upsilon }\,-4{R}^{\aleph \upsilon }{R}_{\aleph \upsilon }+{R}^{2}.$ In $4{\mathbb{D}}$ spacetime, this term is purely topological and does not affect local dynamics, as it is invariant under metric variations with fixed boundary conditions, which means that this factor does not contribute to local dynamics in $4{\mathbb{D}}$ gravity. However, in higher-dimensional spacetimes, the GB term transitions from being a topological invariant to a local term that impacts local dynamics. To account for this transition and manage the term’s influence in higher dimensions, a dimensional regularization approach may be introduced. The following updated action results from rescaling the correlation factor α of the GB component by a factor of $1/({\mathbb{D}}-4)$ as: $\begin{eqnarray}{S}_{\mathrm{EGB}}=\int \left(\displaystyle \frac{{M}_{{\rm{P}}}^{2}\sqrt{-g}}{2}R-\sqrt{-g}{\rm{\Lambda }}+\displaystyle \frac{\sqrt{-g}\alpha }{{\mathbb{D}}-4}{ \mathcal G }\right){{\rm{d}}}^{{\mathbb{D}}}x.\end{eqnarray}$
This rescaling helps extract finite contributions when taking the limit ${\mathbb{D}}\to 4$. In particular, for certain highly symmetric spacetimes, this method effectively cancels out the $({\mathbb{D}}-4)$ factors present in the Einstein equations, leading to finite results in $4{\mathbb{D}}$.If this dimensional regularization technique is valid more generally, it could be applied to other Lovelock terms in ${\mathbb{D}}$-dimensional spacetimes as Lovelock terms are generalized invariants that include the GB factor as a special case, e.g., the Lovelock Lagrangian consists of terms L(n), which are topological in 2n-dimensional spacetimes: $L={\sum }_{n=0}^{t}{L}_{(n)}=\sqrt{-g}{\sum }_{n\,=\,0}^{t}{\alpha }_{n}{R}_{(n)},$ where R(n) are the generalized Euler densities given by ${R}_{(n)}=\tfrac{1}{{2}^{n}}{\delta }_{{\alpha }_{1}{\aleph }_{1}\ldots {\alpha }_{n}{\aleph }_{n}}^{{\aleph }_{1}{\upsilon }_{1}\ldots {\aleph }_{n}{\upsilon }_{n}}{\prod }_{r=1}^{n}{R}^{{\alpha }_{r}{\aleph }_{{\aleph }_{r}}{\upsilon }_{r}}.$ In 2n-dimensional spacetimes, each term L(n) is topological, while in higher dimensions (${\mathbb{D}}\gt 2n$), these terms become local. The contributions of these terms in the equations of motion for ${\mathbb{D}}\gt 2n$ are expected to be proportional to ${\mathbb{D}}-2n$. By rescaling αn accordingly, one can obtain finite local dynamics from terms that would otherwise vanish in lower dimensions.
This approach may also extend to gauge theories where certain terms are topological in specific dimensions but become local in higher dimensions, which is significant in quantum chromo-dynamics. The potential of this dimensional-regularization technique is substantial, but it requires rigorous validation. While Glavan and Lin [27] assume ${\mathbb{D}}\to 4$ limit is the case, explicit proof is still needed. One may discuss the application of this dimensional-regularization approach in the simpler context of $2{\mathbb{D}}$ Einstein gravity which is noted that in $2{\mathbb{D}}$ space-time, and its action contains the term $\sqrt{-g}R$ is a total derivative, similar to the GB term in $4{\mathbb{D}}$ space-time, making the theory trivial unless there is a non-minimal coupling to other fields. When varying the action with respect to the metric, one gets: Λgℵ$v$ = Tℵ$v$, where Tℵ$v$ is the energy-momentum tensor. Extracting the Einstein–Hilbert component in two dimensions yields local dynamics, one can rescale the coupling and take the limit as ${\mathbb{D}}\to 2$. This method avoids reliance on dimensional-regularization prescriptions and offers a more robust theoretical foundation. Let us, now we extend the discussion to special generalization of Einstein gravity with a cosmological constant and anisotropic matter in ${\mathbb{D}}$-dimensions [91] and its action integral described in the following form:7 ) also contains g as the magnitude of metric tensor matter and Lagrangian density (${{ \mathcal L }}_{m}$). Here, coupling constant $\alpha /({\mathbb{D}}-2)$, which is proportional to the scalar curvature R and energy density of the vacuum represented by Λ, which also aids in the Universe’s expansion. Meanwhile α specifies as a finite non-vanishing dimensionless constant that directly links to the coupling strength of the gravitational features. Although its influence is relevant to gravitational dynamics in higher dimensions, this particular factor demonstrates topological invariance in a framework of four dimensions. One may be conceived as modified in the field equations for considered gravitational theory by taking variation of equation (7 ) with respect to the metric tensor which contains Einstein’s cosmological constant, and an additional terms due to ${\mathbb{D}}$-dimensions. To continue our systematic investigation, we consider field equations from [91] that describe Einstein’s field for this modified gravity theory in ${\mathbb{D}}$-dimensions are given as follows:
$\begin{eqnarray}{\mathbb{S}}=\int \left(\displaystyle \frac{\alpha }{{\mathbb{D}}-2}R-{\rm{\Lambda }}+{{ \mathcal L }}_{m}\right)\sqrt{| g| }{{\rm{d}}}^{{\mathbb{D}}}x.\end{eqnarray}$
The action ${\mathbb{S}}$ given in equation ( $\begin{eqnarray}\displaystyle \frac{2\alpha }{{\mathbb{D}}-2}\left({R}_{\aleph \upsilon }+\displaystyle \frac{1}{2}{{Rg}}_{\aleph \upsilon }\right)+{\rm{\Lambda }}{g}_{\aleph \upsilon }={T}_{\aleph \upsilon }.\end{eqnarray}$
The theory under consideration is a special generalization of Einstein gravity with a cosmological constant and anisotropic matter in ${\mathbb{D}}$-dimensions which may be called special case ${\mathbb{D}}$-dimensional modified gravity or ${\mathbb{D}}$-dimensional Einstein gravity, where the gravitational coupling constant κ(−1) is replaced by $\alpha /({\mathbb{D}}-2)$. Taking the limit ${\mathbb{D}}\to 2$ from ${\mathbb{D}}\gt 2$ is subtle and potentially ill-defined because the number of independent components changes discretely (from ${\mathbb{D}}({\mathbb{D}}-1)/2$ to just one in $2{\mathbb{D}}$). The index problem arises since indices cannot take continuous values, making it unclear how to interpret intermediate dimensions like ${\mathbb{D}}=2.1$.It is not crucial whether or not one can extract a factor of ${\mathbb{D}}-2$ from the Einstein tensor. The definition of a tensor Hℵ$v$ for ${\mathbb{D}}\geqslant 3$ is trivial because Hℵ$v$ keeps a similar composition as the Einstein tensor. However, if Gℵ$v$ vanishes while Hℵ$v$ does not in the limit ${\mathbb{D}}=2$, it is puzzling due to their identical tensor structures [91]. Index problems do not exist for scalar formulations, for example the trace of the Einstein equations. Hence, taking the limit ${\mathbb{D}}\to 2$ is straightforward for scalar components. While, for general tensor equations, the situation is more complex. To address this, a $2{\mathbb{D}}$ spacetime is embedded into a higher-dimensional ${\mathbb{D}}$-dimensional space-time, establishing a clear mapping between metric tensor components and Einstein equations in different dimensions. Higher-dimensional models consider the $4{\mathbb{D}}$ space-time to be incorporated in the $5{\mathbb{D}}$ space-time, e.g., building a black hole solution in $4{\mathbb{D}}$ EGB gravity from a $5{\mathbb{D}}$ solution. This raises questions about whether the obtained $4{\mathbb{D}}$ solution accurately describes a black hole in $4{\mathbb{D}}$ or if it is an effective representation of a higher-dimensional solution. For ${\mathbb{D}}\gt 2$, the trace of the modified field equation is given by: $-\alpha R+{\mathbb{D}}{\rm{\Lambda }}=T.$ Taking the limit ${\mathbb{D}}\to 2$, this simplifies to: −αR + 2Λ = T. This simplified equation can describe $2{\mathbb{D}}$ local dynamics if we interpret Λ as an effective cosmological constant derived from higher-dimensional dynamics. In a $3{\mathbb{D}}$ world, the trace equation becomes: −αR + 3Λ(3) = T. Taking the limit ${\mathbb{D}}=3\to 2$ redefines the cosmological constant as: ${\rm{\Lambda }}=\tfrac{3}{2}{{\rm{\Lambda }}}^{(3)}.$ The $R=\tfrac{2{\rm{\Lambda }}}{\alpha }$ is the result of the vacuum solution for a maximally symmetrical geometry in ${\mathbb{D}}$ dimensions. The relation between the cosmological constants in different dimensions depends on the dimensional context.
The non-zero components of field equations describe the gravitational influence of the matter distribution, incorporating the effects of non-static behavior and the anisotropic nature of the matter distribution, considering the directional variations within the ${\mathbb{D}}$-dimensional Einstein gravity framework. Thus, the non-zero components of field equations for the considered sphere system are given as10 ) can be simplified and expressed in an alternative form as shown below
$\begin{eqnarray}\begin{array}{rcl}(\mu +{\rm{\Lambda }}){{\mathbb{E}}}^{2} & = & \displaystyle \frac{2\alpha }{{\mathbb{D}}-2}\left\{\displaystyle \frac{1}{{\mathbb{E}}}\left(\displaystyle \frac{{\mathbb{F}}\dot{{\mathbb{F}}}}{{\mathbb{E}}}+\displaystyle \frac{{{\mathbb{F}}}^{2}\dot{{\mathbb{G}}}}{{\mathbb{EG}}}\right)\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}+\displaystyle \frac{1}{{{\mathbb{G}}}^{2}}{\left(\displaystyle \frac{{\mathbb{F}}}{{\mathbb{G}}}\right)}^{2}\right.\\ & & -\,\left.\left(\displaystyle \frac{{{\mathbb{G}}}^{{\prime} 2}}{{\mathbb{G}}}+2{\mathbb{G}}^{\prime\prime} -\displaystyle \frac{2{{\mathbb{F}}}^{{\prime} }{{\mathbb{G}}}^{{\prime} }}{{\mathbb{F}}}\right)\right\}{\left(\displaystyle \frac{{\mathbb{E}}}{{\mathbb{F}}}\right)}^{2},\end{array}\end{eqnarray}$
$\begin{eqnarray}-2\alpha \left({\dot{{\mathbb{G}}}}^{{\prime} }-\displaystyle \frac{\dot{{\mathbb{F}}}}{{\mathbb{F}}}{{\mathbb{G}}}^{{\prime} }-\dot{{\mathbb{G}}}\displaystyle \frac{{{\mathbb{E}}}^{{\prime} }}{{\mathbb{E}}}\right)\displaystyle \frac{1}{{\mathbb{G}}}=0,\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}({{\mathbb{P}}}_{r}-{\rm{\Lambda }}){{\mathbb{F}}}^{2} & = & -\displaystyle \frac{2\alpha }{{\mathbb{D}}-2}{\left(\displaystyle \frac{{\mathbb{F}}}{{\mathbb{E}}}\right)}^{2}\left\{\displaystyle \frac{2\ddot{{\mathbb{G}}}}{{\mathbb{G}}}+\left\{\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}-\displaystyle \frac{2\dot{{\mathbb{E}}}}{{\mathbb{E}}}\right\}\right.\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}\\ & & -\left.\,{\left(\displaystyle \frac{{\mathbb{E}}}{{\mathbb{F}}}\right)}^{2}\left(\displaystyle \frac{{{\mathbb{G}}}^{{\prime} }}{{\mathbb{G}}}+2\displaystyle \frac{{{\mathbb{E}}}^{{\prime} }}{{\mathbb{E}}}\right)\displaystyle \frac{{{\mathbb{G}}}^{{\prime} }}{{\mathbb{G}}}+{\left(\displaystyle \frac{{\mathbb{E}}}{{\mathbb{G}}}\right)}^{2}\right\},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}({{\mathbb{P}}}_{\perp }-{\rm{\Lambda }}){{\mathbb{G}}}^{2} & = & -\displaystyle \frac{2\alpha }{{\mathbb{D}}-2}\left\{{{\mathbb{EE}}}^{{\prime} }\left(\displaystyle \frac{{{\mathbb{F}}}^{{\prime} }}{{\mathbb{F}}}-\displaystyle \frac{{{\mathbb{G}}}^{{\prime} }}{{\mathbb{G}}}\right)\right.\\ & & -\,{{\mathbb{E}}}^{2}\left(\displaystyle \frac{{\mathbb{E}}^{\prime\prime} }{{\mathbb{E}}}+\displaystyle \frac{{\mathbb{G}}^{\prime\prime} }{{\mathbb{G}}}-\displaystyle \frac{{{\mathbb{F}}}^{{\prime} }}{{\mathbb{F}}}\displaystyle \frac{{{\mathbb{G}}}^{{\prime} }}{{\mathbb{G}}}\right)\\ & & +\,\left.({{\mathbb{F}}}^{2}\dot{{\mathbb{F}}}\dot{{\mathbb{G}}+{{\mathbb{E}}}^{2}{\mathbb{F}}^{\prime} {\mathbb{G}}^{\prime} })\displaystyle \frac{1}{{\mathbb{G}}}\right\}\\ & & \times \,{\left(\displaystyle \frac{{\mathbb{G}}}{{\mathbb{EF}}}\right)}^{2}-\displaystyle \frac{2\alpha }{{\mathbb{D}}-2}{{\mathbb{F}}}^{2}\left(\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}-\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}\displaystyle \frac{\dot{{\mathbb{E}}}}{{\mathbb{E}}}\right.\\ & & -\,\left.\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{F}}}\displaystyle \frac{\dot{{\mathbb{E}}}}{{\mathbb{E}}}+\displaystyle \frac{\ddot{{\mathbb{F}}}}{{\mathbb{F}}}\right){\left(\displaystyle \frac{{\mathbb{G}}}{{\mathbb{EF}}}\right)}^{2}.\end{array}\end{eqnarray}$
After utilizing the expression of the expansion scalar (Θ) and the scalar value of the shear tensor (σ), equation ( $\begin{eqnarray}\displaystyle \frac{2\alpha ({\mathbb{D}}-2)({\mathbb{D}}-3)}{\sigma ({\mathbb{D}}-1)}\left(\displaystyle \frac{{\left({\rm{\Theta }}-\sigma \right)}^{{\prime} }}{\sigma ({\mathbb{D}}-1)}-\displaystyle \frac{{{\mathbb{G}}}^{{\prime} }}{{\mathbb{G}}}\right)=0.\end{eqnarray}$
2.3. Mass function, Bianchi identities and matching conditions
The mass function is presented by Misner and Sharp in [92], which helps to understand the dynamics of compact structures. We compute the mass function for considered relativistic spheres as
$\begin{eqnarray}m={g}^{33}{g}^{44}\displaystyle \frac{{R}^{3}}{2}{R}_{2323}=\displaystyle \frac{{\mathbb{G}}}{2{\mathbb{EF}}}\left[\displaystyle \frac{{\mathbb{F}}}{{\mathbb{E}}}{\dot{{\mathbb{G}}}}^{2}-\displaystyle \frac{{\mathbb{E}}}{{\mathbb{F}}}{{\mathbb{G}}}^{{\prime} 2}+{\mathbb{EF}}\right].\end{eqnarray}$
We get ${m}^{{\prime} }$ as $\begin{eqnarray}{m}^{{\prime} }=\displaystyle \frac{1}{2\alpha }(\mu +{\rm{\Lambda }}){{\mathbb{G}}}^{{\prime} }{{\mathbb{G}}}^{2}.\end{eqnarray}$
Let us now calculate the Bianchi identities, which express the conservation of energy-momentum, i.e., ${T}_{;\upsilon }^{-\aleph \upsilon }{V}_{\aleph }=0$ and ${T}_{;\upsilon }^{-\aleph \upsilon }{\nu }_{\aleph }=0$. Consequently, the non-zero components of these equations are $\begin{eqnarray}-\left\{\dot{\mu }+2\left(\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}+\displaystyle \frac{\dot{{\mathbb{F}}}}{2{\mathbb{F}}}\right)\mu +\displaystyle \frac{\dot{{\mathbb{F}}}{P}_{r}}{{\mathbb{F}}}+2\displaystyle \frac{\dot{{\mathbb{G}}}{{\mathbb{P}}}_{\perp }}{{\mathbb{G}}}\right\}\displaystyle \frac{1}{{\mathbb{E}}}=0,\end{eqnarray}$
$\begin{eqnarray}\left\{{{\mathbb{P}}}_{r}^{{\prime} }+\displaystyle \frac{{{\mathbb{E}}}^{{\prime} }\mu }{{\mathbb{E}}}+2\left(\displaystyle \frac{{{\mathbb{E}}}^{{\prime} }}{2{\mathbb{E}}}+\displaystyle \frac{{{\mathbb{G}}}^{{\prime} }}{{\mathbb{G}}}\right){{\mathbb{P}}}_{r}-2{{\mathbb{P}}}_{\perp }\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}\right\}\displaystyle \frac{1}{{\mathbb{F}}}=0.\end{eqnarray}$
The analysis of junction conditions at discontinuous surfaces plays a fundamental role in gravitational theories. The challenges associated with boundary surfaces are prominently featured in the Schwarzschild and Oppenheimer–Snyder problems, which involve linking the internal gravitational field of a static or collapsing star to the vacuum field outside while junction conditions are critical for ensuring consistent solutions across two distinct space-time regions separated by a hypersurface, denoted by Σ.
The study of discontinuous surfaces is a prominent topic in scientific research. The junction conditions for singular hypersurfaces in GR were first explored by Lanczos [93, 94], while Sen also investigated the connection between the internal and external regions described by the Minkowski and Schwarzschild spacetimes, respectively [95]. His research delved into the significance of the Buchdahl radius in thin-shell configurations and referenced Darmois’ work [96], which aimed to establish junction conditions based on extrinsic and intrinsic curvature to facilitate a smooth connection between the extrinsic and intrinsic regions at Σ.
We will now review the matching conditions with a focus on achieving a smooth transition between two geometries, as emphasized by Mars and Senovilla [97], while some conditions are essential for ensuring proper connections across Σ, which enables the analysis of smooth or thin-shell matches between different spacetimes which is important to note that each modified gravitational theory introduces its own set of matching conditions, whether for smooth transitions or thin-shell cases [98–100]. Our study is concerned with fluid distributions in spherically symmetric systems, where the external boundary is defined by a spherical surface adhering to the smooth matching conditions is essential to discuss gravitational collapse around the fluid configuration.
In this paper, the hypersurface Σ is described as a boundary dividing space-time into two distinct regions and we consider separate metric tensors for the interior and exterior regions, corresponding to the coordinate systems ${x}_{+}^{\aleph }$ and ${x}_{-}^{\aleph }$, respectively. These space-time regions, represented by $({{ds}}_{+}^{2},{g}_{\aleph \upsilon }^{+})$ and $({{ds}}_{-}^{2},{g}_{\aleph \upsilon }^{-})$, each have their own metric ${g}_{\aleph \upsilon }^{\pm }$, where Greek indices take values 0, 1, 2, or 3 (e.g., ℵ, $v$, etc.). It is assumed that coordinates yi are defined on both sides of Σ and Latin indices, such as i and j, ranging over the set {0, 2, 3}, with projection vectors ${e}_{i}^{\aleph }=\partial {x}^{\aleph }/\partial {y}^{i}$. The unit normal vector nℵ is defined across Σ, pointing from the interior to the exterior space-time.
The jump or discontinuity of a physical quantity ${\mathfrak{U}}$ across the surface Σ is represented as follows:
$\begin{eqnarray*}{[{\mathfrak{U}}]={[{{\mathfrak{U}}}^{+}]}_{{\rm{\Sigma }}}-[{{\mathfrak{U}}}^{-}]}_{{\rm{\Sigma }}}.\end{eqnarray*}$
In this scenario, Σ functions as the boundary that separates the interior and exterior regions of space-time, as shown in figure 1. Generally, for a spacetime with nℵ can be expressed as: $\begin{eqnarray*}{n}^{\aleph }\cdot {n}_{\aleph }=\epsilon ({n}^{\aleph })=\left\{\begin{array}{cl}-1; & \mathrm{for}\ {\rm{a}}\ \mathrm{time}-\mathrm{like}\ \mathrm{vector}\ {n}^{\aleph },\\ +1; & \mathrm{for}\ {\rm{a}}\ \mathrm{space}-\mathrm{like}\ \mathrm{vector}\ {n}^{\aleph },\\ 0; & \mathrm{for}\ {\rm{a}}\ \mathrm{null}-\mathrm{like}\ \mathrm{vector}\ {n}^{\aleph }.\end{array}\right.\end{eqnarray*}$
In this expression, ε remains constant across Σ, while we are examining the collapse of a spherical fluid distribution, where the spherical surface Σ(e) represents the boundary of the fluid. Outside a boundary surface Σ(e), we examine the Schwarzschild space-time, where, v, r, θ, and φ represent the coordinates of the metric, which is given as: $\begin{eqnarray}{{\rm{d}}{s}}_{+}^{2}=-\left(1-\displaystyle \frac{2M(\nu )}{r(\nu )}\right){\rm{d}}{\nu }^{2}-2{\rm{d}}{rd}\nu +{r}^{2}{\rm{d}}{{\rm{\Phi }}}_{{\mathbb{D}}-2}^{2}.\end{eqnarray}$
In this instance the delayed time is indicated by ν and the entire mass is represented by M(ν). We analyze a spherically aligned surface which is described by a time-like separating hypersurface in three dimensions. This hypersurface serves as an interface between two four-dimensional manifolds, separating the interior from exterior space-time. Our approach looks at the induced metric of Σ around the throat, which is as follows: $\begin{eqnarray}{{\rm{d}}{s}}_{{\rm{\Sigma }}}^{2}=-{\rm{d}}{\unicode{x000DF}}^{2}+{a}^{2}(\unicode{x000DF})\left({\rm{d}}{\theta }^{2}+{\sin }^{2}\theta \,{\rm{d}}{\phi }^{2}\right)\end{eqnarray}$
The coefficient a(ß) is determined by the appropriate time ß on the throat.
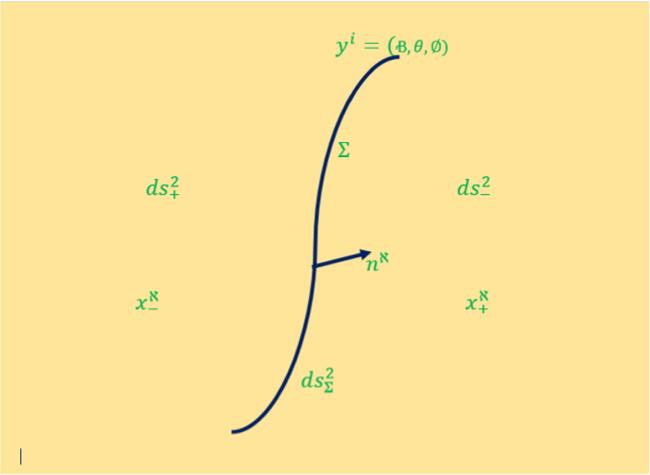
Figure 1. Pictorial representation hypersurface $({{ds}}_{{\rm{\Sigma }}}^{2})$ serves as the boundary separating the interior and exterior regions, denoted by ${{ds}}_{\pm }^{2}$, while normal to this hypersurface is a space-like unit vector nℵ and coordinates on the hypersurface and within the regions ${{ds}}_{\pm }^{2}$ are represented by yi and ${x}_{\pm }^{\aleph }$, respectively [22, 98, 101]. |
With the use of (19 ) and equation (1), the result is18 ) alongside (19 ), we can gain18 ) and equation (1), we obtain the constraint as19 )–(22 ) and (27 ), and inserting the formula $\tfrac{{\rm{d}}{r}}{{\rm{d}}\unicode{x000DF}}=(\tfrac{{\rm{d}}{r}}{{\rm{d}}{t}})(\tfrac{{\rm{d}}{t}}{{\rm{d}}\unicode{x000DF}})$, one receives29 ), we arrive at the mass function M(ν) equation as32 )–(33 ), (19 )–(22 ), as well as (27 ), the result that follows is obtained:29 ), we multiply $\tfrac{-2}{{\mathbb{G}}}$ on both sides of equation (34 ). Rearranging results in the matching constraint that follows as31 ), (35 ), (36 ), and (37 ) by guaranteeing the continuity of the first and second fundamental forms, as described in [96]. It is necessary to assume that the appropriate boundary surface is surrounded by a thin shell if none of these matching requirements are met.
$\begin{eqnarray}{\rm{d}}\unicode{x000DF}\mathop{=}\limits^{{\rm{\Sigma }}}{\mathbb{E}}{dt}\quad \Longrightarrow \quad \displaystyle \frac{{\rm{d}}{t}}{{\rm{d}}\unicode{x000DF}}\mathop{=}\limits^{{\rm{\Sigma }}}{{\mathbb{E}}}^{-1}.\end{eqnarray}$
By combining equation ( $\begin{eqnarray}\left.\begin{array}{c}{\rm{d}}\unicode{x000DF}\mathop{=}\limits^{{\rm{\Sigma }}}\sqrt{\left(1-\displaystyle \frac{2M(\nu )}{r(\nu )}+\displaystyle \frac{2{\rm{d}}{r}}{{\rm{d}}\nu }\right)}{\rm{d}}\nu ,\\ \Longrightarrow \,\displaystyle \frac{{\rm{d}}\nu }{d\unicode{x000DF}}\mathop{=}\limits^{{\rm{\Sigma }}}\displaystyle \frac{1}{\sqrt{\left(1-\tfrac{2M(\nu )}{r(\nu )}+\tfrac{2{dr}}{d\nu }\right)}}.\end{array}\right\}\end{eqnarray}$
By using ( $\begin{eqnarray}{\mathbb{G}}(t,r)\mathop{=}\limits^{{\rm{\Sigma }}}{r}_{{\rm{\Sigma }}}(\nu ).\end{eqnarray}$
With the parametric formulation h(xℵ(yi)), we describe unit normal vector nℵ across the Σ. That being said, the unit normal vector equation follows $\begin{eqnarray}{n}_{\aleph }^{\pm }=\pm \displaystyle \frac{h{,}_{\aleph }}{\sqrt{{g}^{\aleph \upsilon }h{,}_{\aleph }h{,}_{\upsilon }}}=\pm \displaystyle \frac{\partial h}{\partial {x}^{\aleph }}{\left|{g}^{\aleph \upsilon }\displaystyle \frac{\partial h}{\partial {x}^{\aleph }}\displaystyle \frac{\partial h}{\partial {x}^{\upsilon }}\right|}^{\tfrac{-1}{2}},\end{eqnarray}$
In this case, the unit normal is represented in covariant form by nℵ. The components of our geometry are computed using the hypersurface equations, which are as follows: h− = r − rΣ = 0, respectively, h+ = r − rΣ(ν) = 0, leading to $\begin{eqnarray}{n}_{\aleph }^{-}\mathop{=}\limits^{{\rm{\Sigma }}}{\mathbb{F}}(t,r){\delta }_{\aleph }^{1},\end{eqnarray}$
$\begin{eqnarray}{n}_{\aleph }^{+}\mathop{=}\limits^{{\rm{\Sigma }}}\displaystyle \frac{1}{\sqrt{\left(1-\tfrac{2M}{r}+\tfrac{2{\rm{d}}{r}}{{\rm{d}}\nu }\right)}}\left({\delta }_{\aleph }^{1}-\displaystyle \frac{{\rm{d}}{r}}{{\rm{d}}\nu }{\delta }_{\aleph }^{0}\right).\end{eqnarray}$
Consequently, the following definition can be applied to the formula of second basic forms (extrinsic curvature) for interior and exterior manifolds at the hypersurface: $\begin{eqnarray}{{\mathbb{K}}}_{{ij}}^{\pm }=-{n}_{\aleph }^{\pm }\left(\displaystyle \frac{{\partial }^{2}{x}_{\pm }^{\aleph }}{\partial {y}^{i}\partial {y}^{j}}+{{\rm{\Gamma }}}_{\aleph \upsilon }^{\aleph }\displaystyle \frac{\partial {x}_{\pm }^{\aleph }}{\partial {y}^{i}}\displaystyle \frac{\partial {x}_{\pm }^{\upsilon }}{\partial {y}^{j}}\right).\end{eqnarray}$
The Christoffel symbols are indicated in this context by xℵ = (t, r, θ, φ) and ${{\rm{\Gamma }}}_{\aleph \upsilon }^{\aleph }$, while the second fundamental form’s (extrinsic curvature) non-zero constituents are given as: $\begin{eqnarray}\left.\begin{array}{r}{{\mathbb{K}}}_{00}^{-}={\left.-\displaystyle \frac{{\mathbb{E}}^{\prime} }{{\mathbb{EF}}}\right|}_{{\rm{\Sigma }}},\\ {{\mathbb{K}}}_{00}^{+}={\left.-\displaystyle \frac{M}{{r}^{2}}\left(\displaystyle \frac{{\rm{d}}\nu }{{\rm{d}}\unicode{x000DF}}\right)+{\left(\displaystyle \frac{{\rm{d}}\nu }{{\rm{d}}\unicode{x000DF}}\right)}^{-1}\displaystyle \frac{{{\rm{d}}}^{2}\nu }{{\rm{d}}{\unicode{x000DF}}^{2}}\right|}_{{\rm{\Sigma }}},\\ {{\mathbb{K}}}_{22}^{-}={{\mathbb{K}}}_{33}^{-}{\sin }^{-2}\theta ={\left.\displaystyle \frac{{\mathbb{GG}}^{\prime} }{{\mathbb{F}}}\right|}_{{\rm{\Sigma }}},\\ {{\mathbb{K}}}_{22}^{+}={{\mathbb{K}}}_{33}^{+}{\sin }^{-2}\theta ={\left.r\displaystyle \frac{{\rm{d}}\nu }{{\rm{d}}\unicode{x000DF}}\left(1-\displaystyle \frac{2M}{r}\right)+r\left(\displaystyle \frac{{\rm{d}}{r}}{{\rm{d}}\unicode{x000DF}}\right)\right|}_{{\rm{\Sigma }}}.\end{array}\right\}\end{eqnarray}$
In order to determine the mass function constraint, the condition can be thought of as $\begin{eqnarray}{{\mathbb{K}}}_{22}^{+}\mathop{=}\limits^{{\rm{\Sigma }}}{{\mathbb{K}}}_{22}^{-}.\end{eqnarray}$
After applying equations ( $\begin{eqnarray}\displaystyle \frac{1}{{\mathbb{EF}}}\left({\mathbb{G}}^{\prime} -\dot{{\mathbb{G}}}\right)\mathop{=}\limits^{{\rm{\Sigma }}}-{\left(\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{E}}}+\displaystyle \frac{{\mathbb{G}}^{\prime} }{{\mathbb{F}}}\right)}^{-1}\left(\displaystyle \frac{2M}{{\mathbb{G}}}-1\right).\end{eqnarray}$
After resolving equation ( $\begin{eqnarray}M(\nu )\mathop{=}\limits^{{\rm{\Sigma }}}\left(\displaystyle \frac{{\dot{{\mathbb{G}}}}^{2}}{{{\mathbb{E}}}^{2}}+1-\displaystyle \frac{{\mathbb{G}}{{\prime} }^{2}}{{{\mathbb{F}}}^{2}}\right)\displaystyle \frac{{\mathbb{G}}}{2}\mathop{=}\limits^{{\rm{\Sigma }}}\displaystyle \frac{{\mathbb{G}}}{2}\left(1-\displaystyle \frac{{\mathbb{G}}{{\prime} }^{2}}{{{\mathbb{F}}}^{2}}+\displaystyle \frac{{\dot{{\mathbb{G}}}}^{2}}{{{\mathbb{E}}}^{2}}\right).\end{eqnarray}$
So, one may obtain the following constraint as: $\begin{eqnarray}M(\nu )\mathop{=}\limits^{{\rm{\Sigma }}}m(t,r).\end{eqnarray}$
One can use the formula as follows to determine the subsequent junction condition: $\begin{eqnarray}{{\mathbb{K}}}_{00}^{+}={{\mathbb{K}}}_{00}^{-}.\end{eqnarray}$
In this instance, we apply the chain rule to obtain the subsequent constraint, that is to say $\begin{eqnarray}\displaystyle \frac{{{\rm{d}}}^{2}\nu }{{\rm{d}}{\unicode{x000DF}}^{2}}=\displaystyle \frac{{\rm{d}}}{{\rm{d}}{t}}\left(\displaystyle \frac{{\rm{d}}\nu }{{\rm{d}}\unicode{x000DF}}\right)\displaystyle \frac{{\rm{d}}{t}}{{\rm{d}}\unicode{x000DF}}.\end{eqnarray}$
In conjunction with the previously mentioned criterion and the chain rule in equations ( $\begin{eqnarray}\begin{array}{l}{\left(\displaystyle \frac{{\mathbb{G}}^{\prime} }{{\mathbb{F}}}+\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{E}}}\right)}^{-1}\left\{-\displaystyle \frac{M}{{r}^{2}}-\displaystyle \frac{\ddot{{\mathbb{G}}}}{{{\mathbb{E}}}^{2}}-\left(\displaystyle \frac{\dot{{\mathbb{G}}}^{\prime} }{{\mathbb{F}}}-\displaystyle \frac{{\mathbb{G}}^{\prime} \dot{{\mathbb{F}}}}{{{\mathbb{F}}}^{2}}-\displaystyle \frac{\dot{{\mathbb{G}}}\dot{{\mathbb{E}}}}{{{\mathbb{E}}}^{2}}\right)\displaystyle \frac{1}{{\mathbb{E}}}\right\}\\ \qquad \mathop{=}\limits^{{\rm{\Sigma }}}-\displaystyle \frac{{\mathbb{E}}^{\prime} }{{\mathbb{EF}}}.\end{array}\end{eqnarray}$
Once M(ν) has been removed from equation ( $\begin{eqnarray}\displaystyle \frac{{\mathbb{D}}-2}{2\alpha }\left({{\mathbb{P}}}_{r}-{\rm{\Lambda }}\right)\mathop{=}\limits^{{\rm{\Sigma }}}0.\end{eqnarray}$
Therefore, when matching the adiabatic fluid sphere and Schwarzschild space-time, the smooth matching criteria must be satisfied to avoid energy-momentum tensor breakdowns. Additionally, in the coordinates of the external metric, one can obtain the matching constraint on the surface r = rΣ = constant or r = rΣ(ν), and these requirements are given as: $\begin{eqnarray}{\rm{d}}\nu \left(1-\displaystyle \frac{2M(\nu )}{r(\nu )}\right)\mathop{=}\limits^{{\rm{\Sigma }}}{\mathbb{E}}{\rm{d}}{t},\,\,\,{\mathbb{G}}\mathop{=}\limits^{{\rm{\Sigma }}}r(\nu ).\end{eqnarray}$
In order to properly fit the adiabatic fluid sphere to the Minkowski geometry inside the interior empty cavity, the surface separation hypersurface Σ must satisfy certain criteria: $\begin{eqnarray}{{\mathbb{P}}}_{r}\mathop{=}\limits^{{{\rm{\Sigma }}}^{(i)}}0\mathop{=}\limits^{{{\rm{\Sigma }}}^{(i)}}m(t,r).\end{eqnarray}$
The aforementioned circumstances provide a seamless transition between the two zones and show that there is neither pressure nor mass at the border. We were able to meet the matching requirements given in equations (3. Perturbation method
Let us now consider the perturbation technique which is valuable for nonlinear systems of equations to analyze the stable or unstable behavior of the relativistic spheres in our case study. Small perturbations from the equilibrium state of matter distribution are examined, along with the effects of surface pressures, density, and ${\mathbb{D}}$-dimensional modified variables on this compact system’s dynamic behavior. We begin by assuming the fluid is in a static equilibrium state, described in terms of the radial coordinate. It is noticed that the static part of physical entities is denoted by the subscript ‘0’. This assumption allows us to study the metric and material functions with introduced perturbations, expressed as follows:
$\begin{eqnarray}\left\{\begin{array}{l}{X}_{j}(t,r)={X}_{j0}(r)+\epsilon {{\rm{\Phi }}}_{j}(t){x}_{j}(r),\\ \quad m(t,r)={m}_{0}(r)+\epsilon \bar{m}(t,r),\\ {{\mathbb{P}}}_{\perp }(t,r)={{\mathbb{P}}}_{\perp 0}(r)+\epsilon {\bar{{\mathbb{P}}}}_{\perp }(t,r),\,\sigma (t,r)=\epsilon \bar{\sigma }(t,r),\\ \quad \mu (t,r)={\mu }_{0}(r)+\epsilon \bar{\mu }(t,r),\,{\rm{\Theta }}(t,r)=\epsilon \bar{{\rm{\Theta }}}(t,r),\\ {{\mathbb{P}}}_{r}(t,r)={{\mathbb{P}}}_{r0}(r)+\epsilon {\bar{{\mathbb{P}}}}_{r}(t,r).\end{array}\right.\end{eqnarray}$
where, j = 1, 2, 3 also ${X}_{1}={\mathbb{E}}$, ${X}_{2}={\mathbb{F}}$, ${X}_{3}={\mathbb{G}}$, x1 = ψ1, x2 = ψ2, x3 = ψ3, and Φ1 = Φ2 = Φ3 = Φ. To continue our analysis, we consider ${{\mathbb{G}}}_{0}(r)=r$ and 0 < ε ≪ 1. We compute the static parts by using abovementioned perturbation scheme and these parts are given in the appendix section.3.1. Non-static configuration
In this section, we compute the perturbed quantities by utilizing the perturbation scheme defined in (38 ). Consequently, one obtains the non-static parts of modified field equations:16 ) and (17 ) are taken as44 ) yields39 ) and (41 ), along with ${\bar{{\mathbb{P}}}}_{r}\mathop{=}\limits^{{{\rm{\Sigma }}}^{(e)}}0$, as48 ) is given by49 ) represents two separate responses oscillating and non-oscillating functions, which correspond to stable and unstable configurations, respectively. We are particularly interested in studying the unstable aspect of the collapsing spherically symmetric compact fluid system. To do this, we assume that this system initially passes through the static phase and it begins to collapse at t = − ∞, when Φ( − ∞ ) = 0. This behavior can only be described by setting C1 = − 1 and C2 = 0 that meets our requirements, representing the diminishing nature of the solution as time progresses. If ${{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}\lt 0$, oscillations occur, indicating that the system collapses at one point but expands at another. This kind of dynamic pattern, with expansion and contraction induced by oscillations when ${{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}\lt 0$, is not observed in stars throughout their entire lifespan. Thus, our focus is on determining the range of instability, so, we consider the non-oscillating solutions only, to fulfil this condition, we assume ψ1(r), ψ2(r), and ψ3(r) satisfy ${{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}\gt 0$ at the boundary point ${r}_{{{\rm{\Sigma }}}^{(e)}}$. Stars undergo progressive collapse during their later stages to reach their ultimate fate, such as becoming a white dwarf, neutron star, or black hole, which requires ${{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}\gt 0$. To find a real solution to Eq. (48 ) that characterizes collapse, we limit our perturbations to positive definite values, ensuring ${{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}\gt 0$. To analyze the instability of the system, we consider the specific form58 ) as
$\begin{eqnarray}\begin{array}{rcl}\bar{\mu } & = & \displaystyle \frac{4{\rm{\Phi }}\alpha }{{{\mathbb{F}}}_{0}^{2}({\mathbb{D}}-2)r}\left[{\left(\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\right)}^{{\prime} }+r\left(\displaystyle \frac{{{\mathbb{F}}}_{0}^{{\prime} }}{{{\mathbb{F}}}_{0}}-\displaystyle \frac{3}{r}\right){\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime} }\right.\\ & & \left.-\,r{\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime\prime} }+\left(\displaystyle \frac{{\psi }_{2}}{r{{\mathbb{F}}}_{0}}-\displaystyle \frac{{\psi }_{3}}{{r}^{2}}\right){{\mathbb{F}}}_{0}^{2}\right]-2\displaystyle \frac{{\rm{\Phi }}{\psi }_{3}}{{{\mathbb{F}}}_{0}}({\mu }_{0}+{\rm{\Lambda }}),\end{array}\end{eqnarray}$
$\begin{eqnarray}\displaystyle \frac{2\alpha \dot{{\rm{\Phi }}}}{{{\mathbb{E}}}_{0}{{\mathbb{F}}}_{0}}\left[{\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime} }-\displaystyle \frac{{\psi }_{2}}{r{{\mathbb{F}}}_{0}}-\displaystyle \frac{1}{r}-\left(\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}\right)\displaystyle \frac{{\psi }_{3}}{r}\right]=0,\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{\bar{{\mathbb{P}}}}_{r} & = & \displaystyle \frac{2\alpha }{({\mathbb{D}}-2)}\left[-\displaystyle \frac{2\ddot{{\rm{\Phi }}}}{{{\mathbb{E}}}_{0}^{2}}\displaystyle \frac{{\psi }_{3}}{r}+\displaystyle \frac{2{\rm{\Phi }}}{r{{\mathbb{F}}}_{0}^{2}}\left[{\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime} }\left(r\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}+1\right)\right.\right.\\ & & \left.\left.-{{\mathbb{F}}}_{0}^{2}\left(\displaystyle \frac{{\psi }_{2}}{r{{\mathbb{F}}}_{0}}-\displaystyle \frac{{\psi }_{3}}{{r}^{2}}\right)+{\left(\displaystyle \frac{{\psi }_{1}}{{{\mathbb{E}}}_{0}}\right)}^{{\prime} }\right]\right]-\displaystyle \frac{2{\rm{\Phi }}{\psi }_{2}}{{{\mathbb{F}}}_{0}}({{\mathbb{P}}}_{r0}-{\rm{\Lambda }}),\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{\bar{{\mathbb{P}}}}_{\perp } & = & \displaystyle \frac{2\alpha }{({\mathbb{D}}-2)}\left[-\displaystyle \frac{\ddot{{\rm{\Phi }}}}{{{\mathbb{E}}}_{0}^{2}}\left(\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}+\displaystyle \frac{{\psi }_{3}}{r}\right)+\displaystyle \frac{{\rm{\Phi }}}{{{\mathbb{F}}}_{0}^{2}}\left[{\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime\prime} }\right.\right.\\ & & +\,\left(2\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}+\displaystyle \frac{1}{r}-\displaystyle \frac{{{\mathbb{F}}}_{0}^{{\prime} }}{{{\mathbb{F}}}_{0}}\right){\left(\displaystyle \frac{{\psi }_{1}}{{{\mathbb{E}}}_{0}}\right)}^{{\prime} }+{\left(\displaystyle \frac{{\psi }_{1}}{{{\mathbb{E}}}_{0}}\right)}^{{\prime\prime} }-{\left(\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\right)}^{{\prime} }\\ & & \left.\left.\times \,\left(\displaystyle \frac{r{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}+1\right)\displaystyle \frac{1}{r}+\left(\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}-{\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime} }\displaystyle \frac{{{\mathbb{F}}}_{0}^{{\prime} }}{{{\mathbb{F}}}_{0}}+\displaystyle \frac{2}{r}\right)\right]\right]\\ & & -\displaystyle \frac{2{\rm{\Phi }}{\psi }_{2}}{{{\mathbb{F}}}_{0}}({{\mathbb{P}}}_{\perp }-{\rm{\Lambda }}).\end{array}\end{eqnarray}$
The non-static components of Θ and σ are calculated as follows $\begin{eqnarray}\bar{{\rm{\Theta }}}=\left(\displaystyle \frac{2{\psi }_{3}}{r}+\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\right)\displaystyle \frac{\dot{{\rm{\Phi }}}}{{{\mathbb{E}}}_{0}},\,\bar{\sigma }=-\left(\displaystyle \frac{{\psi }_{3}}{r}-\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\right)\displaystyle \frac{\dot{{\rm{\Phi }}}}{{{\mathbb{E}}}_{0}}.\end{eqnarray}$
The non-static configuration of conservation equations, i.e., equations ( $\begin{eqnarray}\displaystyle \frac{\dot{{\rm{\Phi }}}}{{{\mathbb{E}}}_{0}}\left[\dot{\bar{\mu }}+\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\left({{\mathbb{P}}}_{r0}+{\mu }_{0}\right)+2{\psi }_{3}\left(\displaystyle \frac{{\mu }_{0}}{r}+{{\mathbb{P}}}_{\perp 0}\displaystyle \frac{1}{r}\right)\right]=0,\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}\displaystyle \frac{1}{{{\mathbb{F}}}_{0}}\left\{{\left(\displaystyle \frac{{\psi }_{1}}{{{\mathbb{E}}}_{0}}\right)}^{{\prime} }\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right){\rm{\Phi }}+\left({\bar{{\mathbb{P}}}}_{r}+\bar{\mu }\right)\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}+2{\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime} }\right.\\ \quad \left.\times \,\left\{{{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}\right\}{\rm{\Phi }}+{\bar{{\mathbb{P}}}}_{r}^{{\prime} }+\displaystyle \frac{2}{r}\left\{{\bar{{\mathbb{P}}}}_{r}-{\bar{{\mathbb{P}}}}_{\perp }\right\}\right\}=0.\end{array}\end{eqnarray}$
Integration of equation ( $\begin{eqnarray}\bar{\mu }=-\left[\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\left({{\mathbb{P}}}_{r0}+{\mu }_{0}\right)+2{\psi }_{3}\left(\displaystyle \frac{{\mu }_{0}}{r}+{{\mathbb{P}}}_{\perp 0}\displaystyle \frac{1}{r}\right)\right]{\rm{\Phi }}.\end{eqnarray}$
We obtain non-static configuration for mass function as $\begin{eqnarray}\bar{m}=-\displaystyle \frac{{\rm{\Phi }}}{{{\mathbb{F}}}_{0}^{2}}\left[r\left({\psi }_{3}^{{\prime} }-\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\right)+\left(1-{{\mathbb{F}}}_{0}^{2}\right)\displaystyle \frac{{\psi }_{3}}{2}\right].\end{eqnarray}$
To discuss the dynamic behavior of a considered spherically symmetric relativistic system, we obtain the following expression by utilizing equations ( $\begin{eqnarray}\ddot{{\rm{\Phi }}}-{{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}{\rm{\Phi }}\mathop{=}\limits^{{{\rm{\Sigma }}}^{(e)}}0,\end{eqnarray}$
We choose ${{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}(r)$ to be a positive value to make our calculations easier which is given in the appendix. The general solution to equation ( $\begin{eqnarray}{\rm{\Phi }}(t)={C}_{1}\left(\sqrt{{{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}}t\right)+{C}_{2}\left(\sqrt{-{{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}}t\right),\end{eqnarray}$
where C1 and C2 are arbitrary constants. One can observe that the general solution of equation ( $\begin{eqnarray}{\rm{\Phi }}(t)=-\exp \left(\sqrt{{{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}}t\right).\end{eqnarray}$
This shows that as time passes the areal radius reduces and the system continues to collapse. Harrison et al [102] presented the relationship between energy density and source pressures which is given as $\begin{eqnarray}{\bar{{\mathbb{P}}}}_{r}=\bar{\mu }\displaystyle \frac{{{\mathbb{P}}}_{r0}}{{{\mathbb{P}}}_{r0}+{\mu }_{0}}{\rm{\Gamma }}.\end{eqnarray}$
In this context, the adiabatic index Γ is used to measure the change in pressure for a given change in the density of the compact system. It provides information about the stiffness of the fluid. It is important to note that in our discussion the Γ plays a vital role in determining the constraints for instability across the entire fluid distribution. We can obtain the value $\tfrac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}$ from equation ( $\begin{eqnarray}\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}=\displaystyle \frac{1}{2r}\left\{\displaystyle \frac{({\mathbb{D}}-2){{\mathbb{F}}}_{0}^{2}{r}^{2}}{2\alpha }\left({{\mathbb{P}}}_{r0}-{\rm{\Lambda }}\right)+{{\mathbb{F}}}_{0}^{2}-1\right\}.\end{eqnarray}$
3.2. Collapse equation
We compute the collapse equation with the help of non-static parts of the conservation equations and $\tfrac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}$. Additionally, the perturbed components of surface pressures in respective directions are taken into account. One obtains the collapse equation by combining equations (52 ) to (64 ) with equation (45 ), as
$\begin{eqnarray}\begin{array}{l}{\left[\displaystyle \frac{{\rm{\Gamma }}{{\mathbb{P}}}_{r0}}{{\mu }_{0}+{{\mathbb{P}}}_{r0}}\left\{\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right)\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}+2\left({\mu }_{0}+{{\mathbb{P}}}_{\perp 0}\right)\displaystyle \frac{{\psi }_{3}}{r}\right\}\right]}^{{\prime} }\\ \quad -\,\displaystyle \frac{1}{2r}\left(1+\displaystyle \frac{{\rm{\Gamma }}}{{\mu }_{0}+{{\mathbb{P}}}_{r0}}{{\mathbb{P}}}_{r0}\right)\\ \quad \times \,\left\{\displaystyle \frac{({\mathbb{D}}-2){{\mathbb{F}}}_{0}^{2}{r}^{2}}{2\alpha }\left({{\mathbb{P}}}_{r0}-{\rm{\Lambda }}\right)+{{\mathbb{F}}}_{0}^{2}-1\right\}\\ \quad \times \,\left\{\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right)\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}+2\left({\mu }_{0}+{{\mathbb{P}}}_{\perp 0}\right)\displaystyle \frac{{\psi }_{3}}{r}\right\}\\ \qquad +\,\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right){\left(\displaystyle \frac{{\psi }_{1}}{{{\mathbb{E}}}_{0}}\right)}^{{\prime} }\\ \quad -\displaystyle \frac{2{\rm{\Gamma }}}{r}\left(\displaystyle \frac{1}{{\mu }_{0}+{{\mathbb{P}}}_{r0}}{{\mathbb{P}}}_{r0}-\displaystyle \frac{1}{{\mu }_{0}+{{\mathbb{P}}}_{\perp 0}}{{\mathbb{P}}}_{\perp 0}\right)\\ \quad \times \,\left\{\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right)+2\left({\mu }_{0}+{{\mathbb{P}}}_{\perp 0}\right)\displaystyle \frac{{\psi }_{3}}{r}\right\}\\ \quad +\,2\left({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}\right){\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime} }=0.\end{array}\end{eqnarray}$
The significance of the collapse equation lies in its ability to analyze the stable or unstable behavior of relativistic fluid systems at two specific epochs, i.e., N and PN eras. These epochs represent different stages of evolution of considered spherically symmetric systems and are characterized by specific conditions and properties. Via the study of the collapse equation, one can gain insights into the behavior and dynamics of the system at these epochs, specifically in terms of their dynamical stability or instability. This analysis is significant for understanding the overall behavior and fate of the cosmic structures.4. Instability domains
We employed the Chandrasekhar criterion, which is traditionally used to assess the stability of spherically symmetric matter distributions, by evaluating whether the adiabatic index Γ exceeds the critical value of 4/3 in the context of GR and is often used to analyze the stability of compact distribution like neutron stars and white dwarfs. In the context of ${\mathbb{D}}$-dimensional modified gravity, its validity requires careful consideration while fundamental principles underlying his criterion rely on the balance between internal pressure and gravitational forces. In higher-dimensional theories, such as those considered in ${\mathbb{D}}$-dimensional modified gravity, the additional spatial dimensions introduce new curvature terms and modify the gravitational interactions which can affect both the form of the field equations and the resulting stability conditions.
To address this, we have analyzed the stability of spherically symmetric matter distributions within the ${\mathbb{D}}$-dimensional modified gravity framework, where our approach involves extending this usual criterion to account for the additional curvature effects introduced by the higher-dimensional gravity. Specifically, we have incorporated the modifications to the field equations and the resulting changes in the effective pressure and density terms due to which new conditions appear for stability that reflect the impact of ${\mathbb{D}}$-dimensional curvature terms. While Γ remains a crucial factor, its role is adjusted by the additional components introduced by the modified gravity theory thus, the criterion still provides a meaningful measure of stability, but with considerations for the higher-dimensional effects that could alter the critical value or stability conditions and we discussed these aspects more comprehensively.
The structural evolution of stellar systems and many such compact systems are currently in a non-linear state due to their higher densities compared to the Universe’s average densities. To fully understand their evolution, it is important to examine their linear or quasi-linear phases while numerous mathematical methods exist to explore the dynamics of non-linear celestial systems, and these methods do not solve all issues but offer valuable insights. In modified gravities, the complex gravitational field equations can be simplified by applying linear perturbations, which help determine the stability of these compact formations and one may use co-moving coordinates for analysis, which align with the near-homogeneity of large-scale cosmic structures. These challenges arise due to the nonlinearity of dynamical equations and the absence of a background geometry to consider certain physical quantities. To overcome these challenges and obtain reliable results, approximation techniques are utilized. One such technique is linearized gravity, which approximates the nonlinear aspects of space-time metrics, leading to acceptable conclusions. This approach facilitates the handling of linearized field equations that describe weak gravitational fields. Consequently, the N and PN constraints in gravitational theories are commonly considered approximations applicable to weak field conditions. In the following sub-sections, we examine the stability criteria of celestial geometry in both the N and PN eras under the influence of ${\mathbb{D}}$-dimensional modified gravity theory via theoretical and graphical approaches.
4.1. N and PN approximations
In situations where relativistic effects are minimal, the N approximation is used to simplify the problem by assuming weak gravitational fields and low velocities relative to the speed of light. This approximation is also applicable in regions with weak gravitational fields, such as those far from massive objects, where there are little differences between the relativistic and N predictions. Although the PN framework is utilized when velocities are closer to the speed of light or gravitational fields are stronger, it also takes into consideration higher-order effects and extends the N framework to include relativity corrections. It is also applicable to higher-dimensional gravities. Thus, the transition from the N to the PN framework usually happens when the system’s velocity or the strength of the gravitational field reaches relativistic scales, and certain thresholds or criteria can be established depending on the parameters of the system. The N framework does not account for the generation and propagation of gravitational waves, which are important in relativistic contexts while PN theory includes these effects, making it necessary for a complete description in certain scenarios.
In this particular subsection, we consider our established collapse equation to evaluate the system effectively, while confining our focus to the N domain in the background of ${\mathbb{D}}$-dimensional modified gravity. In this domain, we consider the collapse equation against a flat background characterized by the metric coefficients, i.e., ${{\mathbb{E}}}_{0}=1$ and ${{\mathbb{F}}}_{0}=1$. The stability of a gravitating stellar fluid configuration is influenced by an inequality that is established for Γ. This inequality plays a critical role in comprehending the system’s dynamical instability. Furthermore, we discuss the criteria for instability by applying significant constraints to this derived inequality for the adiabatic index, and to the static components of the energy density (μ0) and surface pressures (${{\mathbb{P}}}_{r0}$ and ${{\mathbb{P}}}_{\perp 0}$). The constraints we impose are as follows ${{\mathbb{P}}}_{r0}\ll {\mu }_{0}$ and ${{\mathbb{P}}}_{\perp 0}\ll {\mu }_{0}$, indicating that the radial pressure and tangential pressure are considerably smaller than the energy density. Additionally, we observe that $\tfrac{{{\mathbb{P}}}_{r0}}{{\mu }_{0}}\to 0$ and $\tfrac{{{\mathbb{P}}}_{\perp 0}}{{\mu }_{0}}\to 0$. By considering the collapse equation at the N epoch while adhering to the aforementioned constraints, we can gain further insights into the behavior exhibited by the system. So the collapse equation becomes54 ). The study concludes that the spherically compact system remains stable if it does not satisfy the conditions outlined in (54 ). The instability range, as defined by the adiabatic index, depends on pressure components, anti-gravitational forces, and the radial features of energy density and anisotropy within the context of D-dimensional modified gravity. One can observe as follows:
$\begin{eqnarray}{\rm{\Gamma }}\lt \displaystyle \frac{\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right){\psi }_{1}^{{\prime} }-\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)({{\mathbb{P}}}_{r0}-{\rm{\Lambda }})+2({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}){\left(\tfrac{{\psi }_{3}}{r}\right)}^{{\prime} }}{{\left({{\mathbb{P}}}_{r0}\left({\psi }_{2}-\tfrac{2{\psi }_{3}}{r}\right)\right)}^{{\prime} }-\left(\tfrac{2}{r}({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0})+\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }{\rm{\Lambda }}\right)\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)}.\end{eqnarray}$
In this study, a flat background metric was used to analyze the dynamical instability conditions for spherically symmetric fluid configurations with locally anisotropic interiors at N era. It was found that for instability, the energy density of the compact matter must be significantly greater than the pressure components in respective directions, leading to constraints where pressure components are negligible compared to density. To determine stability, each term in the collapse equation must be positive, and the hydrodynamic equation must match the form specified by equation (| • | The system will be in hydrostatic equilibrium if the gravitational forces $| \left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right){\psi }_{1}^{{\prime} }\,-\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)({{\mathbb{P}}}_{r0}-{\rm{\Lambda }})+2({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}){\left(\tfrac{{\psi }_{3}}{r}\right)}^{{\prime} }| $ are balanced by the anti-gravitational and effective pressure forces $| {\left({{\mathbb{P}}}_{r0}\left({\psi }_{2}-\tfrac{2{\psi }_{3}}{r}\right)\right)}^{{\prime} }-\left(\tfrac{2}{r}({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0})+\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }{\rm{\Lambda }}\right)\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)| .$ |
| • | If the forces generated by $| \left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right){\psi }_{1}^{{\prime} }\,-\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)({{\mathbb{P}}}_{r0}-{\rm{\Lambda }})+2({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}){\left(\tfrac{{\psi }_{3}}{r}\right)}^{{\prime} }| $ exceed those from $| {\left({{\mathbb{P}}}_{r0}\left({\psi }_{2}\,-\tfrac{2{\psi }_{3}}{r}\right)\right)}^{{\prime} }-\left(\tfrac{2}{r}({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0})+\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }{\rm{\Lambda }}\right)\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)| $, the system will achieve a stable state rather than collapsing, indicating that counter-gravitational forces and effective pressures satisfy the stability condition Γ > 1. |
| • | Conversely, if the contribution from $| \left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right){\psi }_{1}^{{\prime} }\,-\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)({{\mathbb{P}}}_{r0}-{\rm{\Lambda }})+2({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}){\left(\tfrac{{\psi }_{3}}{r}\right)}^{{\prime} }| $ is less than the contribution from $| {\left({{\mathbb{P}}}_{r0}\left({\psi }_{2}-\tfrac{2{\psi }_{3}}{r}\right)\right)}^{{\prime} }-\left(\tfrac{2}{r}({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0})+\tfrac{({\mathbb{D}}-2){\mu }_{0}r}{4{\psi }_{1}\alpha }{\rm{\Lambda }}\right)\left({\psi }_{2}+\tfrac{2{\psi }_{3}}{r}\right)| $, the system will become unstable, with the adiabatic index Γ may fall within the open interval (0, 1). |
Let us now discuss our systematic investigation focuses to examine the dynamical instability exhibited by spherically symmetric fluid structures in the PN domain with ${\mathbb{D}}$-dimensional modified gravity. In the PN domain the metric coefficients ${{\mathbb{E}}}_{0}$ and ${{\mathbb{F}}}_{0}$ are taken as ${{\mathbb{E}}}_{0}=1-\tfrac{{m}_{0}}{r}$ and ${{\mathbb{F}}}_{0}=1+\tfrac{{m}_{0}}{r}$. By employing PN approximation, we can investigate the relativistic consequences up to an order of $O\left(\tfrac{{m}_{0}}{r}\right)$. Under these assumptions regarding the metric coefficients, our established collapse equation undergoes modification, enabling the computation of the inequality for adiabatic index Γ. Thus, under these conditions, the collapse equation turns out to be
$\begin{eqnarray}{\rm{\Gamma }}\lt \displaystyle \frac{\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right){\left({\psi }_{1}{\mathbb{X}}\right)}^{{\prime} }-\tfrac{1}{2r}\left[\tfrac{({\mathbb{D}}-2){r}^{2}}{2\alpha }{\mathbb{X}}({{\mathbb{P}}}_{r0}-{\rm{\Lambda }})+\tfrac{2{m}_{0}}{r}\right]{\mathbb{Y}}+2({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}){\left(\tfrac{{\psi }_{3}}{r}\right)}^{{\prime} }}{{\left(\tfrac{{{\mathbb{P}}}_{r0}{\mathbb{Y}}}{{\mu }_{0}+{{\mathbb{P}}}_{r0}}\right)}^{{\prime} }+\tfrac{{{\mathbb{P}}}_{r0}{\mathbb{Y}}}{2r({\mu }_{0}+{{\mathbb{P}}}_{r0})}\left(\tfrac{({\mathbb{D}}-2){r}^{2}}{2\alpha }{\mathbb{X}}({{\mathbb{P}}}_{r0}-{\rm{\Lambda }})+\tfrac{2{m}_{0}}{r}\right)+\tfrac{2{\mathbb{Y}}}{r}{\mathbb{Z}}},\end{eqnarray}$
where, the full form of ${\mathbb{X}},\,{\mathbb{Y}}$ and ${\mathbb{Z}}$ are given in the appendix section.The study assumes specific conditions on metric coefficients to analyze the instability of an spherically symmetric compact fluid configuration in the PN domain. The role of extra curvature terms arising from ${\mathbb{D}}$-dimensional modified gravity, along with material and metric functions, is emphasized in maintaining the stability or instability of the compact formation. We applied specific conditions to the metric coefficients to examine the instability of an considered compact sphere symmetric fluid configuration in the PN domain. We reorganized the collapse equation for this scenario. The study also derives an inequality for the adiabatic index that is crucial for instability in the PN era with ${\mathbb{D}}$-dimensional modified gravity.
Finally, the text notes that the dynamical instability of compact matter configurations is linked to phases of hydrostatic equilibrium. The ${\mathbb{D}}$-dimensional modified gravitational field equations, which couple matter with gravitational interactions, play a key role in these equilibrium frameworks. The additional curvature features introduced by the modified gravity help mitigate instability, and standard GR solutions can be retrieved by excluding these additional factors under specific limits. We present the figures to include comparative plots that clearly show the stability results from both approximations which will help illustrate the regions where the N approximation is valid and where deviations occur.
4.2. Graphical interpretation
We study the dynamical instability of relativistic spherically symmetric structures in which the matter sector is supported by anisotropic distribution under the formalism of ${\mathbb{D}}$-dimensional modified gravity. It is worth noting that in this paper, we compute the collapse equation from the non-static parts of conservation equations via the Harrison et al [102] EoS at N and PN epochs. In our systematic investigation, we start by considering the hydrostatic profile, which enters into the non-static phase with linear perturbation parameters. To investigate the collapsing phase of anisotropic sphere configuration, certain constraints for stability must be considered. The adiabatic index determines the stability criteria for the study of symmetric collapsing formations.
We use pictorial illustrations to figure out the un/stable behavior of the evaluated spherically symmetric structure across the N and PN periods. We summarized all pertinent findings regarding both eras that proved to be noteworthy for particular values of Λ and various values of parameter α. This demonstrates the importance of the stiffness parameter and supports the conclusions made by Chandrasekhar [57]. Additionally, we investigate the effects of matter and ${\mathbb{D}}$-dimensional modified gravitation factors on the dynamical unstable criteria. Examining Chandrasekhar’s findings demonstrates the importance of the adiabatic index in establishing the instability. Specifically, it established that for a system to remain stable, the value of Γ should be greater than $\tfrac{4}{3}$, and if Γ is less than $\tfrac{4}{3}$, then the system becomes unstable. This observation underscores the importance of understanding and accurately calculating the adiabatic index in various physical systems. The schematic diagrams in figures 2 and 3 show pictorial illustrations of our considered ${\mathbb{D}}$-dimensional modified gravitational model for stable and unstable behavior at N and PN eras, respectively.
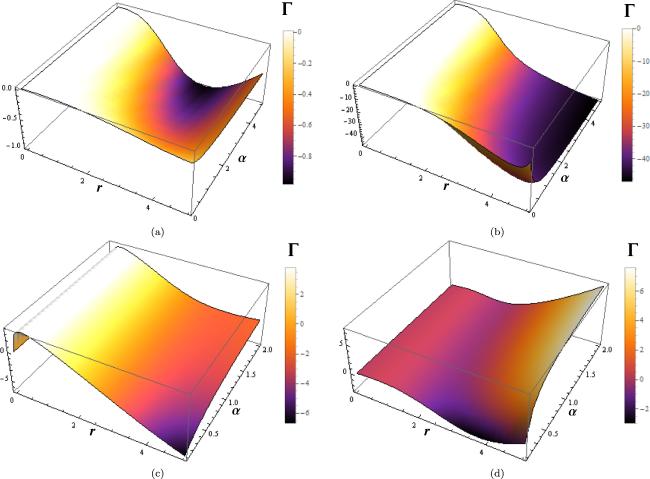
Figure 2. Pictorial representation for the dynamical behavior of non-static relativistic sphere models under the influence of ${\mathbb{D}}$-dimensional modified gravity at N epoch. |
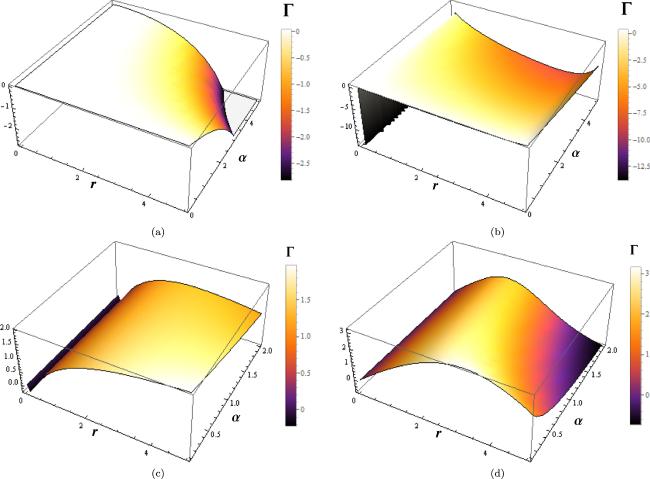
Figure 3. Diagrammatic representations of the spherically aligned relativistic sphere’s unstable and stable behavior over a range of values for different parameters at the PN era. |
Each subfigure represents under specific parameter settings and we agree that a more thorough comprehension of our findings requires a clarified explanation of these features. To represent our results graphically, we shall concentrate on the N and PN approximations. It is important to acknowledge that identifying the ranges of dynamical instability becomes challenging in the absence of a singular parameter like Γ. The presence of various physical attributes of the fluid, including pressure anisotropy and the energy density radial profile, has a considerable impact on the scope of instability. One may examine that in this situation, it is not possible to fully capture the behavior of spherically symmetric fluid with just a single parameter. Instead, multiple factors come into play and interact with each other to determine the overall instability range. These factors are intrinsic properties of the fluid and are intimately connected to its internal structure. Therefore, analyzing the instability range requires a detailed understanding of the fluid’s structural properties. To initiate instability, it is necessary to fulfill the conditions established in the equations (54 )–(55 ). To determine whether instabilities occur, we must consider the positivity of the all terms of these constraints. If these terms are positive, it can lead to instabilities. For this condition to hold the range of instability depends upon the positive values of Pr0 − P⊥0, 5Pr0 − 2P⊥0. In other words, the system approaches the instability ranges for Pr0 > P⊥0, Pr0 > 2/5P⊥0 and the other term in equations (54 )–(55 ) must also be positive. Let us delve deeper into this possibility graphically.
For graphical analysis, we should consider an energy density distribution that follows the pattern of μ0 = λrn and ${\psi }_{i}^{,s}={\eta }_{i}^{,s}r$, where λ and ${\eta }_{i}^{,s}$ are a positive constants and n is also a constant that can have any value from negative infinity to positive infinity. When we substitute this expression into equations (54 )–(55 ), the one of the terms in the equation will take a specific form, but only if N is not equal to negative three. When this energy density profile is plugged into equations (54 )–(55 ), a term in the equation will be affected by the value of N and the statement clarifies that this effect only applies if N is not equal to negative three. In other words, the value of N affects the equation in a specific way, but only if it does not equal negative three.
We summarize our findings here:
| • | In figures 2(a) and (b), we used the Newtonian (N) framework. For figure 2(a), the parameters are ${\eta }_{i}^{,s}$, with values η1 = 0.4, η2 = 0.6, and η3 = 0.8, along with λ = 1.2 and Λ = 0.5. For figure 1(b), the parameters are ${\eta }_{i}^{,s}$, where η1 = 0.5, η2 = 0.8, and η3 = 1.1, with λ = 1.5 and Λ = 1.1. While some parameters remain consistent between figures 2(a) and (b), such as ${\mathbb{D}}=3$, n = 1.5, and the fixed range of α ∈ (0, 5) shown in both figures, the ranges of the adiabatic index Γ differ due to the varying parameter values used in each case. |
| • | In figures 3(a) and (b), we applied the PN framework. For figure 3(a), the parameters used are: ${\eta }_{i}^{,s}$, with specific values η1 = 0.5, η2 = 0.6, and η3 = 0.7, along with λ = 1.3, and Λ = 0.7. In figure 3(b), the parameters are ${\eta }_{i}^{,s}$, where η1 = 0.3, η2 = 0.8, and η3 = 1.1, with λ = 2.5, and Λ = 1.5. Although some parameters are consistent between figures 3(a) and (b), such as ${\mathbb{D}}=3$, n = 1.5, and the fixed range of α ∈ (0, 5) shown in both panels, the PN regime introduces additional parameters or corrections, like ${\mathbb{X}}$, ${\mathbb{Y}}$, and ${\mathbb{Z}}$, due to relativistic effects. This leads to variations in the range of the adiabatic index Γ, which differs as Γ ∈ (0, − 3) in figure 3(a) and Γ ∈ (0, − 12) in figure 3(b). |
| • | Next in the N domain, one observes from figure 2 stable and unstable regions for the specific sets of parameters, i.e., n = 3.5, λ = 1.35 Λ = 1.3, ${\mathbb{D}}=4$ and different values ${\eta }_{i}^{,s}$ for (c) and also different values ${\eta }_{i}^{,s}$, n = 5.5, λ = 1.45, Λ = 1.6 and ${\mathbb{D}}=5$ in (d) and the range of α ∈ (0, 2) in both panels (c) and (d) of figures 2. |
| • | We observe from figure 2 in the PN era, some stable and unstable regions for the specific sets of parameters, i.e., m0 = 1.5, n = 2.5, λ = 2.55, Λ = 1.2 ${\mathbb{D}}=4$ and different values ${\eta }_{i}^{,s}$ for (c) and also different values ${\eta }_{i}^{,s}$, with m0 = 2.0, n = 4.5, λ = 4.5, Λ = 1.4 and ${\mathbb{D}}=5$ in (d) and the range α is α ∈ (0, 2) in both panels (c) and (d) of figures 3. |
| • | Additionally, it is noted that in both scenarios, the adiabatic index ranges are marginally different. In these Figs, we find a relatively small stable zone in contrast to the unstable graphical representations. By taking into account the some specific choice of parametric values at N and PN eras, the figures 2 and 3 are obtained, which show the systematic graphical behavior of spherically symmetric compact system with ${\mathbb{D}}$-dimensional modified gravity theory. |
5. Summary of work
In this work, we investigated the significant dynamical conditions for maintaining the instability of spherically symmetric fluid configuration that undergoes adiabatic collapse with ${\mathbb{D}}$-dimensional modified gravity. This non-static spheres system assumed to be supported with the anisotropic matter. We developed a systematic approach in which conservation equations and modified field equations under the influence of ${\mathbb{D}}$-dimensional modified gravity model are established. In the considered framework, α is a coupling non-vanishing dimensionless constant in ${\mathbb{D}}$-dimensional modified gravity and considered as a correction to GR. We also computed the expression for Misner and Sharp mass function, important kinematical variables, expansion scalar, and junction conditions with the framework considered gravity theory.
The field equations in ${\mathbb{D}}$-dimensional modified gravity are very complex and finding out their exact or general solutions is still a challenging question. To avoid these discrepancies, one may use the linear perturbation method. For such stellar structures, this technique is useful in estimating their evolution and dynamic instabilities. A linear perturbation methodology to the metric as well as matter parameters was employed to study the dynamical unstable behavior. In the beginning, we assumed our considered compact system is stationary, but eventually, it shifted into a dynamic phase where the metric coefficients show time dependency. By varying field equations up to the first order in the perturbation parameter and perturbing portions of conservation equations, we were able to derive the collapse equation. These consequences are achieved through the underlying assumption that all metric functions present within the static background exhibit positive values.
In order to carry out our systematic study, we examine that certain conditions are applied to the collapse equation, which yields significant physical effects. The study of dynamical instability in the N and PN realms with ${\mathbb{D}}$-dimensional modified gravity and an expanding requirement revealed that the adiabatic index Γ determines the degree of instability. This index characterizes the fluid’s stiffness in general and, in our case study, it performs an important role in defining the instability ranges. In both the N and PN regimes, we went into considerable detail about the dynamical instability criterion for anisotropic sphere structures under a few key physical assumptions related to the mathematical expression of Γ. Our observations show that our considered compact object’s stability changes over its evolution depending on several material variables, including anisotropic pressure, ${\mathbb{D}}$-dimensional modified gravity parameters, and energy density profiles.
We explore the instability of spherically symmetric fluid structures with anisotropic matter in a D-dimensional modified gravity framework, considering both flat and curved backgrounds across N and PN regimes. Our findings indicate that instability arises when the energy density of the matter exceeds the surface pressure components along their respective axes, under specific constraints applied to the metric coefficients and physical variables. The analysis reveals that the anisotropic stellar system remains unstable if certain inequalities hold true. Key factors influencing this instability include the radial distribution of energy density, anisotropy, and other curvature components due to the gravitational effects considered. The following is a short recap of our findings:
These constraints incorporate the positive energy density to ensure energy conservation. We illustrated the stable and unstable behavior of the sphere system via schematic representation at the N and PN eras. A range for the adiabatic index less than the typical value of stiffness parameter for an unstable sphere structure, i.e., $\tfrac{4}{3}\gt {\rm{\Gamma }}$, was the sole feature that was seen in panels (a) and (b) of figures 2 and 3. Panels (c) and (d) of both figures represent the stable and unstable behavior for specific values of different parameters. We investigated the ranges of the adiabatic index appearing slightly different in both cases. Additionally, all of the instability constraints computed by the study are compatible with the findings presented by GR under the standard constraints.
| • | It is important to note that the results in equations ( |
| • | Many of the additional curvature components introduced by ${\mathbb{D}}$-dimensional modified gravity in equations ( |
| • | We identified two key relations for the adiabatic index in equations ( |
| • | We established that when the system’s stiffness parameter equals the right-hand sides of relations ( |
| • | Consequently, the inequalities in equations ( |
Acknowledgments
This research is supported by Researchers Supporting Project number: RSPD2024R650, King Saud University, Riyadh, Saudi Arabia (BA).
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix
This section contains the necessary intermediate computations needed to perform the methods of deduction and evaluations that are presented in the main body of the paper. Applying the condition from equation (4 ) as follows will readily yield an alternative form of Bianchi identity defined in equation (16 ) as38 ). Thus, we obtain a static section of field equations as16 ) and (17 ), which provides the following expressions46 ) in (51 ) as55 ), are written as
$\begin{eqnarray}\dot{\mu }+{\rm{\Theta }}({{\mathbb{P}}}_{r}+\mu ){\mathbb{E}}+\displaystyle \frac{\dot{{\mathbb{G}}}}{{\mathbb{G}}}(2{{\mathbb{P}}}_{\perp }-2{{\mathbb{P}}}_{r})=0.\end{eqnarray}$
We compute static parts of modified field equations, the Bianchi identities, and mass functions by using the perturbative approach defined in equation ( $\begin{eqnarray}{\mu }_{0}+{\rm{\Lambda }}=\displaystyle \frac{2\alpha }{({\mathbb{D}}-2){\left({{\mathbb{F}}}_{0}r\right)}^{2}}\left(2r\displaystyle \frac{{{\mathbb{F}}}_{0}^{{\prime} }}{{{\mathbb{F}}}_{0}}+{{\mathbb{F}}}_{0}^{2}-1\right),\end{eqnarray}$
$\begin{eqnarray}{{\mathbb{P}}}_{r0}-{\rm{\Lambda }}=\displaystyle \frac{2\alpha }{({\mathbb{D}}-2){\left({{\mathbb{F}}}_{0}r\right)}^{2}}\left(2r\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}-{{\mathbb{F}}}_{0}^{2}+1\right),\end{eqnarray}$
$\begin{eqnarray}{{\mathbb{P}}}_{\perp 0}-{\rm{\Lambda }}=\displaystyle \frac{2\alpha }{({\mathbb{D}}-2){{\mathbb{F}}}_{0}^{2}}\left[\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime\prime} }}{{{\mathbb{E}}}_{0}}-\displaystyle \frac{{{\mathbb{F}}}_{0}^{{\prime} }}{r{{\mathbb{F}}}_{0}}-\displaystyle \frac{{{\mathbb{F}}}_{0}^{{\prime} }}{{{\mathbb{F}}}_{0}}\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}\right.\left.+\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{r{{\mathbb{E}}}_{0}}\right].\end{eqnarray}$
We investigate the static structure of the Bianchi identities as equations ( $\begin{eqnarray}{{\mathbb{P}}}_{r0}^{{\prime} }+\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right)\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}+\displaystyle \frac{2}{r}\left({{\mathbb{P}}}_{r0}-{{\mathbb{P}}}_{\perp 0}\right)=0.\end{eqnarray}$
The static configuration for mass function may be written as $\begin{eqnarray}{m}_{0}=\displaystyle \frac{r}{2}\left(1-\displaystyle \frac{1}{{{\mathbb{F}}}_{0}^{2}}\right).\end{eqnarray}$
Consequently, the value of ${{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}}$ is given as $\begin{eqnarray}\begin{array}{rcl}{{\rm{\Psi }}}_{{{\rm{\Sigma }}}^{(e)}} & = & \displaystyle \frac{1}{{\psi }_{3}}\left[{\left(\displaystyle \frac{{{\mathbb{E}}}_{0}}{{{\mathbb{F}}}_{0}}\right)}^{2}\left[{\left(\displaystyle \frac{{\psi }_{1}}{{{\mathbb{E}}}_{0}}\right)}^{{\prime} }+\left(r\displaystyle \frac{{{\mathbb{E}}}_{0}^{{\prime} }}{{{\mathbb{E}}}_{0}}+1\right){\left(\displaystyle \frac{{\psi }_{3}}{r}\right)}^{{\prime} }\right.\right.\\ & & \left.\left.-\,\displaystyle \frac{{{\mathbb{F}}}_{0}^{2}}{r}\left(\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}-\displaystyle \frac{{\psi }_{3}}{r}\right)\right]-\displaystyle \frac{({\mathbb{D}}-2)}{2\alpha }\displaystyle \frac{{{\mathbb{E}}}_{0}r{\psi }_{2}{\rm{\Lambda }}}{{{\mathbb{F}}}_{0}}\right].\end{array}\end{eqnarray}$
One easily computes the non-static parts of the surface in respective directions, by using equations ( $\begin{eqnarray}{{\mathbb{P}}}_{r0}=\displaystyle \frac{{\rm{\Gamma }}{\rm{\Phi }}}{{\mu }_{0}+{{\mathbb{P}}}_{r0}}{{\mathbb{P}}}_{r0}\left\{\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right)\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}+2\left({\mu }_{0}+{{\mathbb{P}}}_{\perp 0}\right)\displaystyle \frac{{\psi }_{3}}{r}\right\},\end{eqnarray}$
$\begin{eqnarray}{{\mathbb{P}}}_{\perp 0}=\displaystyle \frac{{\rm{\Gamma }}{\rm{\Phi }}}{{\mu }_{0}+{{\mathbb{P}}}_{\perp 0}}{{\mathbb{P}}}_{\perp 0}\left\{\left({\mu }_{0}+{{\mathbb{P}}}_{r0}\right)\displaystyle \frac{{\psi }_{2}}{{{\mathbb{F}}}_{0}}+2\left({\mu }_{0}+{{\mathbb{P}}}_{\perp 0}\right)\displaystyle \frac{{\psi }_{3}}{r}\right\}.\end{eqnarray}$
The value of ${\mathbb{X}},\,{\mathbb{Y}}$ and ${\mathbb{Z}}$, which appear in ( $\begin{eqnarray*}\begin{array}{rcl}{\mathbb{X}} & = & 1+\displaystyle \frac{2{m}_{0}}{r},\\ {\mathbb{Y}} & = & {\psi }_{2}({\mu }_{0}+{{\mathbb{P}}}_{r0})\left(1-\displaystyle \frac{{m}_{0}}{r}\right)+2({\mu }_{0}+{{\mathbb{P}}}_{\perp 0})\displaystyle \frac{{\psi }_{1}}{r},\\ {\mathbb{Z}} & = & \displaystyle \frac{{{\mathbb{P}}}_{r0}}{{\mu }_{0}+{{\mathbb{P}}}_{r0}}-\displaystyle \frac{{{\mathbb{P}}}_{\perp 0}}{{\mu }_{0}+{{\mathbb{P}}}_{\perp 0}}.\end{array}\end{eqnarray*}$