1. Introduction
Bose–Einstein condensate (BEC) is an interesting and important phenomenon that occurs in a certain system of most atoms at ultra-low temperatures. It is a unique state of matter that was first predicted by Bose and Einstein [1]. Wieman and Cornell observed BEC in 87Rb atomic gases using laser cooling and evaporative cooling techniques in magnetic traps [2]. Later, Ketterle’s group also achieved BEC of 23Na in an experiment [3]. A team led by Jin realized the condensation of 40K in 2004 [4]. Then BEC provides an ideal platform for studying superfluid phenomena [5–7].
A Kármán vortex street is a well-known phenomenon in classical fluid systems. When the fluid flows past an obstacle, vortex pairs with opposite rotating directions and regular arrangement are formed, and this wake is called a Kármán vortex street [8–11]. As a long-lived topological excitation, it has a vital effect on understanding the properties of superfluids [12]. The phenomenon of Kármán vortex streets has also been found in quantum fluids [13]. In 2010, Sasaki et al studied a Kármán vortex street formed by moving obstacle potential in the scalar BEC [14]. Saito et al found that the vibration of the obstacle potential plays a modulating role in the formation of vortex streets in 2013 [15]. In the experiment, Kwon et al observed different wake patterns in oblate atomic BEC under various velocities of the obstacle [16]. Furthermore, the Kármán vortex street in a two-component and spin-orbit coupled BEC is investigated as well [17, 18].
Parity-time (PT) symmetry was initially proposed by Bender and Boettcher in 1998, and it has garnered significant attention [19]. Their result shows that the energy spectrum associated with non-Hermitian operators maintains a fully real character [20–22]. Usually, an open quantum system takes into account the the imaginary part of the external potential to contribute a gain and loss model [23]. The atoms loss can be induced by a focused electron beam [24] while atoms are added by letting them fall into the condensate from a second condensate [25]. For satisfying the necessary but not sufficient condition of a PT symmetric potential. Its real part exhibits even symmetry, whereas the imaginary part is an odd one [26]. In addition, the similarity between the Schr $\ddot{{\rm{o}}}$ dinger equation in quantum mechanics and the mean-field Gross–Pitaevskii (GP) equation sparked study into BEC under the influence of PT symmetric potentials [27, 28]. In 2017, Lukas Schwarz et al investigated vortex excitations in a dilute BEC with the complex PT symmetric potential [29]. Haag et al studied nonlinear quantum dynamics in a double well potential satisfying PT-symmetry, where particles are injected into one well and removed from the other [30, 31]. Recently, researchers have delved deeply into the study of vortex and solitons excitations caused by PT symmetric potentials in BEC systems [32–34]. However, the Kármán vortex street is rarely studied in a system with PT symmetric potential. Thus, it is worth investigating the generation of the Kármán vortex street and exploring the impact of gain-loss strength on its stability in system.
In this paper, we numerically found that the Kármán vortex street can be generated when the width and moving velocity of the obstacle potential are appropriate. The numerical simulation results also include typical combined modes. When the Kármán vortex street is generated, the amplitude of the drag force acting on the obstacle potential increases first and then decreases. By analyzing the influence of the imaginary part of the PT symmetric potential on the motion trajectory of vortex pairs behind the obstacle potential, it is found that the motion trajectory of the vortex pairs gradually changes from V-shaped to the Kármán vortex street. Consequently, it is worth investigating the generation of the Kármán vortex street and exploring the impact of gain-loss strength.
2. Theoretical method
The Hamiltonian of the BEC with PT symmetric potential can be written as [35–37]
$\begin{eqnarray}H=\int {\rm{d}}{\boldsymbol{r}}{\psi }^{\dagger }\left(-\displaystyle \frac{{{\hslash }}^{2}}{2m}{{\rm{\nabla }}}^{2}+V+\displaystyle \frac{1}{2}g{\psi }^{\dagger }\psi \right)\psi ,\end{eqnarray}$
where ψ = ψ(r, t) denotes the wave function of the condensate. r = (x, y, z) represents the Cartesian coordinate, t indicates time. ∇2 is a three-dimensional Laplacian operator. The PT symmetric potential V = VR + iVI, where VR and VI are the real and imaginary parts of the external potential. VI can influence the atomic distribution in the BEC. Total particles are N = ∫∣ψ∣2dr. g = 4πℏ2as/m is the interaction strength between atoms, as stands for the s-wave scattering length [38–40].In the experiments, BEC is usually confined within a harmonic potential ${V}_{\mathrm{har}}=\tfrac{1}{2}m\left({\omega }_{x}^{2}{x}^{2}+{\omega }_{y}^{2}{y}^{2}+{\omega }_{z}^{2}{z}^{2}\right)$, here ωx, ωy and ωz denote the respective frequencies of the potential along x, y and z directions. When confinement is stronger in the z-direction than in the other two directions, the energy scale of ℏωz is much larger than ℏωx and ℏωy [41–45]. Thus the ‘disk-shaped’ condensate is formed in the xy plane. Under which, the wave function is reasonably represented as $\psi ({\boldsymbol{r}},t)=\varphi (x,y,t){\phi }_{0}(z){{\rm{e}}}^{-{\rm{i}}{\omega }_{z}t/2}$, indicating that the motion of atoms along the z-direction is confined to the ground state which is expressed as ${\phi }_{0}{(z)=(m{\omega }_{z}/\pi {\hslash })}^{1/4}{{\rm{e}}}^{-m{\omega }_{z}{z}^{2}/2{\hslash }}$.
In the following, we introduce the characteristic time ${t}_{0}={\omega }_{0}^{-1}$ and characteristic length ah0 to facilitate the research. The corresponding variables in equation (1 ) are normalized by $\tilde{t}={\omega }_{0}t$, $\tilde{x}=x/{a}_{{\rm{h}}0}$, $\tilde{y}=y/{a}_{{\rm{h}}0}$, $\tilde{\psi }\,=\psi /\sqrt{{n}_{0}/{a}_{{\rm{h}}0}^{2}}$, $\tilde{g}=4\pi {n}_{0}{a}_{s}/\sqrt{2\pi }{l}_{z}$, $\tilde{V}=V/{\hslash }{\omega }_{0}$ with ${\omega }_{0}\,=\min ({\omega }_{x},{\omega }_{y})$, ${l}_{z}=\sqrt{{\hslash }/m{\omega }_{z}}$ and ${a}_{{\rm{h}}0}=\sqrt{{\hslash }/m{\omega }_{0}}$. n0 represents the characteristic particle number density. For simplicity, The tilde ‘∼’ has been omitted from all the variables. Therefore, the dimensionless quasi-two-dimensional GP equation is derived as
$\begin{eqnarray}{\rm{i}}\displaystyle \frac{\partial \psi }{\partial t}=\left[-\displaystyle \frac{1}{2}{{\rm{\nabla }}}^{2}+V+g| \psi {| }^{2}\right]\psi .\end{eqnarray}$
The ground state is obtained by adopting the initial state through the use of the imaginary-time propagation method. The initial guess is assumed to be ψ = 1 and Γ is set to be zero. Without loss of generality, we take g = 1. Otherwise, it can be reduced to 1 by appropriate mathematical transformation. The symmetry of the system is intentionally disturbed by introducing a small stochastic perturbation. The time-splitting Fourier pseudo-spectral method is employed to numerically solve equation (2 ) under periodic boundary conditions [46]. The spatial domain is truncated to [−256, 256] ⨂[−64, 64] and discretized uniformly into 2048 × 512 grids.
3. Numerical results
To satisfy the condition that the real part of the PT symmetric potential is an even function and the imaginary part is an odd one, we choose the real part to be the Gaussian obstacle potential, which is given by [14]
$\begin{eqnarray}{V}_{{\rm{R}}}={V}_{0}\left[{{\rm{e}}}^{-\tfrac{{\left(x-{x}_{0r}+\upsilon t\right)}^{2}+{\left(y+{y}_{0r}\right)}^{2}}{{d}^{2}}}+{{\rm{e}}}^{-\tfrac{{\left(x+{x}_{0r}-\upsilon t\right)}^{2}+{\left(y-{y}_{0r}\right)}^{2}}{{d}^{2}}}\right],\end{eqnarray}$
where V0 is the peak strength. (x0r, y0r) represents the center position of VR at t = 0. The imaginary part of the PT symmetric potential is adopted as [29] $\begin{eqnarray}{V}_{{\rm{I}}}={\rm{\Gamma }}\left[{{\rm{e}}}^{-\tfrac{{\left(x-{x}_{0i}\right)}^{2}+{\left(y+{y}_{0i}\right)}^{2}}{{d}^{2}}}-{{\rm{e}}}^{-\tfrac{{\left(x+{x}_{0i}\right)}^{2}+{\left(y-{y}_{0i}\right)}^{2}}{{d}^{2}}}\right].\end{eqnarray}$
Here, Γ is the gain-loss strength. (±x0i, ± y0i) expresses the center position that remains stationary during the dynamical evolution. d denotes the width of VI and VR. The harmonic potential is no longer considered here.In practice, the Gaussian obstacle potential VR centered at (x0r, y0r) = (204.8, 25) begins to move along −x direction with $v$, while another obstacle moves along the x direction. We investigate various wake patterns by adjusting d and $v$ of the obstacle potential. Figure 1 denotes the wake pattern of the drifting vortex dipoles and V-shaped vortex pairs. The direction of the moving obstacle potential is indicated by the black arrows. Vortex pairs will periodically shed behind the obstacle when $v$ exceeds a critical value [47]. The width of the obstacle and the interaction between atoms affects the critical velocity. Vortex pair shedding reduces the primary velocity to below the critical velocity. After a brief period, the primary velocity field is larger than the critical velocity again, causing a new vortex pair to be shed. When d = 0.5 and $v$ = 0.56, the drifting vortex dipoles are generated behind the obstacle potential (see in figure 1(a)). This is a new wake pattern in the system. It is specified that + represents the clockwise rotation and − symbolizes the counterclockwise rotation. Two vortices exhibit opposite circulation ±2πℏ/m, which is consistent with dimensionless circulation ±2π. The vortex dipoles undergo drift and it is evident that their centers are not distributed along a single line. This indicates that the vortex pairs are not stable and the local density distribution of the particle is unequal in the system. In figure 1(b), vortex-antivortex pairs are emitted alternately behind the obstacle when $v$ increases to 0.65. The distance between two point vortices keeps almost unvaried in the process of dynamic evolution. The vortex-antivortex pairs are unstable and form the V-shaped vortex pair.
Figure 1. Density (left panel) and phase (right panel) distribution of the condensate at different velocity $v$ for d = 0.5. (a) $v$ = 0.56. (b) $v$ = 0.65. The direction of the moving obstacle potential is indicated by the black arrows. The + indicates clockwise circulation of the vortex and − represents counterclockwise circulation. |
When the velocity of the obstacle potential is 0.49 and the width increases from 1.8 to 2.1, Kármán vortex street and irregular turbulence appear behind the obstacle potential, as shown in figure 2. Although there is gain and loss of atoms in the system, vortex pairs are alternately and periodically released from the obstacle potential. The upper and lower vortex pairs have opposite circulations ±2π. The wake eventually becomes the Kármán vortex street (see figure 2(a)). The angular frequency of the vortex is 2ℏ/(mD2) [48], where D refers to the distance between two vortices center. The average distance between two rows of vortex pairs is b ≈ 29.25, and between adjacent vortex pairs in one row is l ≈ 135.50. So the ratio is b/l ≈ 0.22. In [49], the stability condition for generating the Kármán vortex street in classical fluids satisfies 0.12 < b/l < 0.4. Therefore, our result falls into this range and agrees well with the conclusion. If d increases to 2.1, while $v$ remains at 0.49, vortex pairs form irregular turbulence (see figure 2(b)). It is found that the wake tends to be irregular turbulence when the width of the obstacle potential increases.
Figure 2. The density (left panel) and phase (right panel) distribution of the condensate at different d for $v$ = 0.49. (a) d = 1.8. (b) d = 2.1. The black straight arrows show the direction in which the obstacle is moving. The black curved arrows represent the direction of circulations of vortex pairs. |
A variety of combined modes are also present in the system with PT symmetric potentials. Figure 3 plots V-shaped vortex pairs and irregular turbulence, which are combined with the Kármán vortex street, respectively. Figure 3(a) represents the combined mode of the Kármán vortex street and V-shaped vortex pairs. Unlike the case of the V-shaped vortex pairs (see figure 1(b)), the distance between two adjacent vortex pairs becomes larger. We note that the Kármán vortex street has been formed when the obstacle moves along −x direction. In figure 3(b), we find that irregular turbulence exists when the obstacle moves in the x direction. In figure 3, the ratio is b/l ≈ 0.20 with b ≈ 28.75 and l ≈ 146.63 on average, which is within the range of stability condition. It is worth noting that the combined modes have not occurred in the scalar BEC system which is without PT symmetric potential. The combined mode is asymmetric because of the broken local symmetry caused by gain and loss of atoms. One can come to the conclusion that the density distribution of particles has important effects on the local symmetry of the system.
Figure 3. Density (left panel) and phase (right panel) distribution of combined modes. (a) (d, $v$) = (1.7, 0.45), (b) (d, $v$) = (1.7, 0.51). |
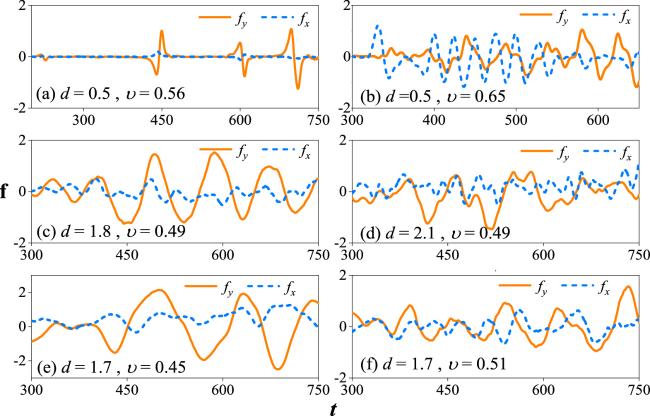
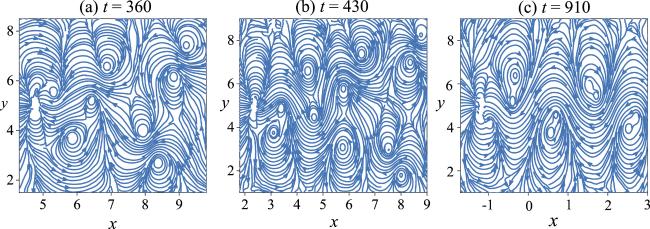
The drag force experienced by the moving obstacle potential is defined as f = (fx, fy) = i∂t∫ψ*∇ψdxdy. Figure 4 indicates a normalized instantaneous drag force when the vortex is released from the obstacle. Figure 4(a) illustrates the drag force corresponding to the drifting vortex dipoles. fx is the shedding frequency of vortices. fy represents the frequency at which the vortex pair moves in an upward or downward direction. It is noticed that the drag force oscillates periodically and the amplitudes are not equal. As the vortex pairs behind the obstacle do not shed simultaneously, and the frequencies of the motion of the vortex pairs along the y direction are inconsistent. Figure 4(b) describes the drag force of the V-shaped vortex pairs plotted in figure 1(b). When the vortex pairs shed, the oscillating trajectory of the drag force has a certain periodicity. fx exhibits periodic oscillations within the range of approximately 388.18 to 514.84 for t. It indicates that the vortex pairs, which are generated by the moving obstacle potentials along both the x direction and the −x direction, simultaneously shed off in the same direction. 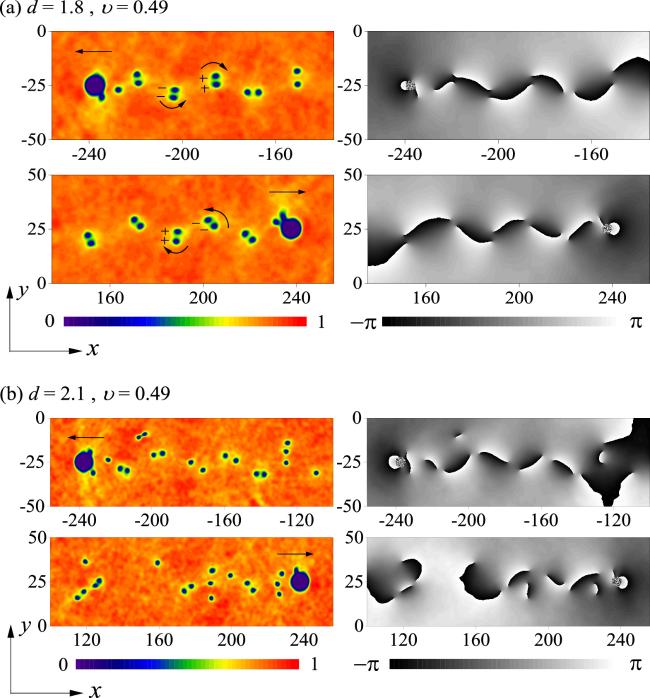Figure 4(c) corresponds to the Kármán vortex street. fy oscillates periodically, and it is noteworthy that the amplitude of fy tends to increase then decrease. When the shedding of vortices is irregular turbulence (see figure 2(b)), the drag force has no obvious periodicity, as shown in figure 4(d). Figures 4(e) and (f) correspond to combined modes of the Kármán vortex street and V-shaped vortex pair (see figure 3(a)), and the Kármán vortex street and irregular turbulence (see figure 3(b)). It is found that fy has obvious periodicity, indicating that there exists periodic shedding vortex pairs. One can observe a clear difference in the frequency and magnitude between this system and the scalar BEC lacking PT-symmetry potential.
Figure 4. The variation of the instantaneous drag force with vortex shedding. The blue dashed line and the orange solid line correspond to fx and fy. |
Figure 5 depicts the parametric region of different wake patterns. When the moving velocity of the obstacle potential is low, a laminar flow is generated. Irregular turbulence generally occurs when the velocity is larger. There is a green area indicating the Kármán vortex street, in which the range of width and velocity is 1.1 < d < 3.2 and 0.39 < $v$ < 0.54. As opposed to other vortex patterns, it is noticed that the combined modes (red area in figure 5) are scattered around the range of the Kármán vortex street.
Figure 6 shows dynamic evolutions of the vortex structures with various gain-loss strengths. For Γ = 0.1, the persistently stable Kármán vortex street appears, as shown in figure 6(a). As Γ increases to 0.3, the vortex street tends to disappear in figure 6(b). It is also observed that irregular vortices are formed when the wake is close to the obstacle potential. In figure 6(c), the distances between two point vortices in partial vortex pairs increase at Γ = 0.5 and the vortices become irregular. As the gain-loss strength Γ increases, the vortex structure pattern changes.
Figure 6. Density distribution for d = 1.6, $v$ = 0.48. (a) Γ = 0.1, (b) Γ = 0.3, (c) Γ = 0.5. |
To better understand the impact of the imaginary part of the PT symmetric potential on the evolution of the Kármán vortex street, figure 7 shows the probability current density vector field behind the obstacle potential. The wake generated by the obstacle potential moving in the x direction is similar to that produced by one moving in the opposite direction. Thus, ignoring the situation where obstacles move along the x direction. At t = 360, the obstacle potential is far from the imaginary part (in figure 7(a)). That is, the vortex pairs are almost unaffected by the gain-loss strength, forming V-shaped vortex pairs. It is evident that the circulation between the vortex pairs is opposite. Figure 7(b) exhibits the wake when the obstacle enters the influence region of the imaginary part. The atomic number is uneven, breaking the symmetry within this range and leading to the probability current density vector field changes. Furthermore, it alters the track of vortices, evolving the V-shaped vortex pair into the Kármán vortex street. As time evolution goes on, the obstacle moves away from the position of the imaginary part, while the gain-loss strength exerts a diminished influence on vortices. The probability current density vector field keeps almost unchanged behind the obstacle. Eventually, the Kármán vortex is generated, as shown in figure 7(c).
Figure 7. The probability current density vector field distribution at different times for d = 1.6, $v$ = 0.48. The obstacle potential moves along the −x direction. The arrows denote the direction of the probability current density vector field. |
For a deeper understanding of how the PT symmetric potential affects the system dynamics, figure 8 focuses on the density distribution of the Kármán vortex street generated in systems with or without PT symmetric potential for d = 1.8 and $v$ = 0.49. The black dashed circle outlines the Kármán vortex street formed after the moving obstacle. Figure 8(a) depicts vortex pairs alternately released from the obstacle potential in a scalar BEC without PT symmetric potential (the model is same as in [14]), forming a neatly Kármán vortex street. Figures 8(b) and (c) shows the density distribution for our model with Γ = 0 or Γ = 0.1. As can be seen from figure 8(b), the short segment of Kármán vortex street is formed behind the obstacle potential moving along the x or −x directions, respectively. Figure 8(c) demonstrates the Kármán vortex street generated behind the PT symmetric potential when gain-loss strength Γ = 0.1. During the same evolutionary period, the number of vortex pairs constituting the Kármán vortex street in figure 8(c) is the least compared to figures 8(a) and (b), implying that the imaginary part of the PT symmetric potential is unfavorable for the formation of the Kármán vortex street.
Figure 8. The density distribution of the condensate past the obstacle potential with or without PT symmetric potential. (a) Kármán vortex street formed in a scalar BEC. The model is the same as that in [14]. (b) Γ = 0 for our model. (c) Γ = 0.1 for our model. (d = 1.8, $v$ = 0.49). |
In order to observe the Kármán vortex street with PT symmetric potential in experiment, we propose a potential approach for implementation. We consider that the BEC is composed of 87Rb atoms, and its hyperfine state is ∣f = 1, mf = –1⟩ [50] with m ≈ 1.45 × 10−25 kg. The total number of atoms in condensed matter is N ≈ 6.55 × 106(n0 = 100). The condensate is confined in a harmonic potential with (ωx, ωy, ωz) ≈ 2π × (43, 56, 350) Hz [51]. Thus ω0 = 2π × 43 Hz and the oscillator length is ${a}_{\mathrm{ho}}=\sqrt{{\hslash }/m{\omega }_{x}}\approx 3.6\,{\rm{\mu }}$m. We adjust as to be approximately equal to 54.22aB [52]. Here, aB is the Bohr radius. The interaction strength between atoms g ≈ 2.74 × 10−51 J. The repulsive laser beam excites Gaussian obstacle potential along the z-direction [53–55]. It moves with $v$ ≈ 0.099 mms−1 from the initial position (x0, y0) = (0.74, 0.09) mm along the −x direction and (x0, y0) = ( − 0.74, − 0.09) mm along the opposite direction, respectively. The peak intensity is V0 ≈ 5.88 × 10−31 J. The width of the PT symmetric potential is d ≈ 6.47μm and the gain-loss strength is Γ ≈ 5.88 × 10−34 J. In the experiment, an atomic laser injects atoms into a condensate to obtain gain [56]. By utilizing a laser beam to excite atoms into excited states and subsequently use photon recoil to eject them from the condensate [25]. Thus, the parameters are approximate figure 2(a) and the Kármán may be achieved.
4. Conclusion
We have simulated the dynamics of the vortex released from a PT symmetric potential. By varying the width and velocity of the real part of PT symmetric potential, we observed that the potential moving at a constant velocity exhibits various wake patterns. The ratio b/l for Kármán vortex street is slightly below the stability criterion in classical fluid theory. We also calculate the drag force experienced by the obstacle. In contrast to the scalar BEC without PT symmetric potential, the drag force exhibits different frequencies and magnitudes. We numerically found the parameter regions of different vortex shedding modes. Meanwhile, the velocity field after the obstacle potential is also affected by the imaginary part of the PT symmetric potential. We explored that the imaginary part can introduce additional asymmetry in the system. It alters the shedding frequency and the trajectory of the vortex, thus influencing the generation of the Kármán vortex street. We proposed an experimental solution which is relevant to the parameters in figure 2(a). The research may enhance the exploration of other fluid dynamics issues.