Tunnel conductance spectroscopy is an effective tool to study the transport properties in tunnel junctions composed of superconductors and non-superconducting materials. As a crucial factor in determining the features of the tunnel conductance spectra, the proximity effect in superconducting tunnel structures, such as normal metal/insulator/superconductor (NM/I/SC), NM/ferromagnetic insulator (FI)/SC, ferromagnetic metal (FM)/I/SC, FM/FI/SC, etc, has been extensively studied theoretically and experimentally [1–10]. The results reveal that Andreev reflection, as a unique charge transport process, plays a dominant role in the proximity effect and thus largely determines the transport properties of superconducting heterostructures [11]. For example, in FM/SC bilayers, because the spins of the electrons and Andreev reflection holes in the FM layer are opposite, the interference between the wave functions describing the two types of particles leads to damped oscillations of the superconducting order parameter F(x) in FM induced by proximity effects [12, 13]. The states of the superconducting junction corresponding to positive F(x) and negative F(x) are usually called ‘0 state’ and ‘π state’, respectively. It has been reported that in FM/s-wave SC and d-wave SC tunnel junctions, the density of states (DOS) in the FM layer near the FM and SC interface change from ‘0 state’ to ‘π state’ as the ferromagnetic layer thickness increases [14–16]. Since the DOS is usually experimentally measured by tunnel conductance spectrum, the inversion of tunnel conductance spectrum has become one of the hot topics in the study of transport properties of superconducting heterostructures.

Another important application of tunneling spectroscopy is to study and identify the symmetry of the electron pair potential in high critical temperature (T_C) superconductors [17–19]. For example, for d-wave symmetry and [110] orientation, that is the ${d}_{{x}^{2}-{y}^{2}}$ -wave symmetry, both theory and experiment show that the tunneling spectra of different types of superconducting junctions have a zero-bias conductance peak (ZBCP) [20–22]. However, the determination of mixed waves ${d}_{{x}^{2}-{y}^{2}}+is$ and ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ and the tunnel spectral characteristics are still a physical problem to be solved. Theoretical studies based on the weakly coupled Bardeen–Cooper–Schrieffer theory have shown that a second phase transition to ${d}_{{x}^{2}-{y}^{2}}+is$ or ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ superconducting state may occur at low temperatures if pairing interactions in the subdominant pair potential s-wave or ${d}_{xy}$ -wave component are large enough [23]. Other theoretical studies pointed out that the subdominant pair potential breaks the time-reversal symmetry, resulting in the splitting of the ZBCP of the conductance spectrum [24]. At the same time, an experiment has reported that for the [110] scanning tunneling microscopy junction, the ${d}_{{x}^{2}-{y}^{2}}+is$ mix-wave split the ZBCP [25]. Another experiment [26] has shown that splitting is also observed, but it is uncertain whether it is ${d}_{{x}^{2}-{y}^{2}}+is$ or ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave. However, the experiment in [27] showed that for ${d}_{{x}^{2}-{y}^{2}}+is$ -wave and [110] orientation, the height of the ZBCP became zero. It can be seen that the ZBCP splitting caused by time-reversal symmetry breaking (TRSB) still needs further experimental and theoretical research. This is one of our objectives. The second reason is that although the quasiparticle lifetime problem is mentioned in [27], no relevant theoretical studies have been seen so far.

In this paper, two types of mixed wave SC pairing potentials ${d}_{{x}^{2}-{y}^{2}}+is$ and ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ are chosen. The wave functions of quasiparticles in different regions of NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave and NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave SC tunnel junctions are obtained according to the Bogoliubov–de Gennes (BdG) equation [28]. Applying the extended Blonder–Tinkham–Klapwijk (BTK) theoretical method [29], the analytical expression of the tunneling conductance is given. Based on these results, we discuss the influence of the TRSB state, proximity effects and quasiparticle lifetime on the transport properties in the considered superconducting tunnel junctions.

The superconducting tunnel junction under consideration consists of three layers, NM, FM and SC, which are successively distributed in the x < 0, 0 < x < L and x > 0 regions. There is an insulating barrier between the NM and the FM with a position coordinate of x = 0 and strength of U. The thickness of the FM is L and the exchange energy in the FM is described by h.

Considering the finiteness of tunneling quasiparticle lifetime, the superconducting coherence factor is given by [30] ${u}^{2}=1-{v}^{2}=\displaystyle \frac{1}{2}\left(1+\sqrt{1-{\left|\displaystyle \frac{{\rm{\Delta }}}{\varepsilon +i{\rm{\Gamma }}}\right|}^{2}}\right),$ where $\varepsilon $ is the excitation energy of tunneling quasiparticles, ${\rm{\Gamma }}=\hslash /\tau $ with $\tau $ the tunneling quasiparticle lifetime, and ${\rm{\Delta }}$ is the symmetry of the superconducting pairing potential.

The specific forms of the two superconducting pairing potentials ${d}_{{x}^{2}-{y}^{2}}+is$ and ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave are written as [31]:Here, ${\theta }_{S}$ and $\alpha $ are the angles between the normal of the interface between FM and SC and the momentum of the transport quasiparticles in the SC and the a-axis of the superconducting crystal, ${{\rm{\Delta }}}_{D},{{\rm{\Delta }}}_{s}$ and ${{\rm{\Delta }}}_{d}$ correspond to the amplitude of the ${d}_{{x}^{2}-{y}^{2}}$ -wave, s-wave, and ${d}_{xy}$ -wave superconducting states, respectively.

To simplify the discussion, in this paper we assume that the form of the effective single-particle Hamiltonian for NM, FM and SC is the same, written as $H=-\tfrac{{\hslash }^{2}}{2m}\tfrac{{{\rm{d}}}^{2}}{{\rm{d}}{x}^{2}}+V-{E}_{{\rm{F}}}$ with m the mass of quasiparticles, V the static potential, and ${E}_{{\rm{F}}}$ the Fermi energy.

When a beam of electrons with upward spin in the NM is incident on the insulating interface at an angle $\theta $ and spin–flip scattering is ignored, the BdG equation satisfied by the electron and hole excitations can be written in the following form [28]:Here, $\bar{\sigma }$ is the spin opposite to $\sigma ,$ $\sigma =+(-)$ stands for spin up(down) and ${\eta }_{\sigma }=1$ for $\sigma =+$ and ${\eta }_{\sigma }=-1$ for $\sigma =-.$

The wave functions of the tunneling particles satisfying equation (2) in the three regions of NM, FM and SC are respectively given as follows:Here, ${n}_{\pm }={k}_{F}\pm m\varepsilon /\left({\hslash }^{2}{k}_{F}\right)$ with ${k}_{F}=\sqrt{2m{E}_{{\rm{F}}}}/{\hslash }^{2},$ ${k}_{\pm }\,={k}_{F}^{\pm }\pm m\varepsilon /\left({\hslash }^{2}{k}_{F}\right)$ with ${k}_{F}^{\pm }={k}_{F}\sqrt{1\pm h/{E}_{{\rm{F}}}},$ and ${p}_{\pm }={k}_{F}\,\pm m\sqrt{{\varepsilon }^{2}-{{\rm{\Delta }}}^{2}}/\left({\hslash }^{2}{k}_{F}\right)$ are respectively the wave vectors of NM, FM and SC. All the coefficients a, b, c₁ ∼ c₆ can be obtained by solving the continuity equations ${\psi }_{NM}\left(0\right)={\psi }_{FM}\left(0\right),$ ${\psi }_{FM}\left(L\right)\,={\psi }_{SC}\left(L\right),$ ${\psi }_{FM}^{{\prime} }\left(0\right)-{\psi }_{NM}^{{\prime} }\left(0\right)=\frac{2mU}{{\hslash }^{2}}{\psi }_{NM}\left(0\right),$ and ${\psi }_{FM}^{{\prime} }\left(L\right)={\psi }_{SC}^{{\prime} }\left(L\right)$ satisfied by the wave functions and their derivatives.

On the basis of the above results and defining the spin polarization of FM as ${P}_{+}=1-{P}_{-}=\tfrac{{E}_{{\rm{F}}}-h}{2{E}_{{\rm{F}}}},$ the analytical expression for differential tunneling conductance of NM/I/FM/${d}_{{x}^{2}-{y}^{2}}+is$ -wave and NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave SC tunnel junctions can be defined as [32]:

Since experimental studies on the transport properties of superconducting tunnel junctions are usually completed by measuring the relationship between normalized tunnel conductance and bias voltage (eV) [33], in order to obtain the results of this study in future experiments, we normalize the tunnel conductance by its value at $eV=2{{\rm{\Delta }}}_{0}$ with ${{\rm{\Delta }}}_{0}$ the maximum energy gap of SC in the following discussion. At the same time, we take the thickness of ferromagnetic layer L = 5 nm and $\alpha =0.25\pi $ to indicate the interface normal of the SC along the direction [110].

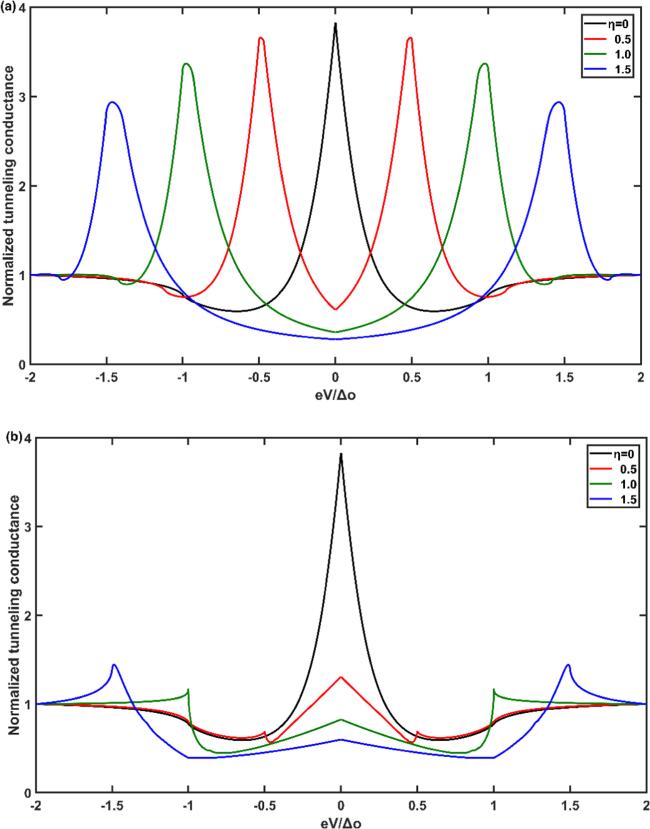
We first discuss the effect of the TRSB on the normalized tunnel conductance. The results are given in figure 1, where (a) and (b) are two plotted cases of ${d}_{{x}^{2}-{y}^{2}}+is$ -wave and ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave, respectively. As can be seen from the two figures, when $\eta =\displaystyle \frac{{{\rm{\Delta }}}_{s}}{{{\rm{\Delta }}}_{D}}\left(\displaystyle \frac{{{\rm{\Delta }}}_{d}}{{{\rm{\Delta }}}_{D}}\right)=0,$ as a typical characteristic of ${d}_{{x}^{2}-{y}^{2}}$ -wave and [110] orientation, the ZBCP is obtained. This ZBCP indicates the existence of a zero-energy Andreev bound state (ABS) of superconducting tunnel junction. The formation of ABS is explained physically as follows. From equation (1), it can be seen that when $\eta =\displaystyle \frac{{{\rm{\Delta }}}_{s}}{{{\rm{\Delta }}}_{D}}\left(\displaystyle \frac{{{\rm{\Delta }}}_{d}}{{{\rm{\Delta }}}_{D}}\right)=0$ and $\alpha =0.25\pi ,$ the pair potential for injected quasiparticles and reflected quasiparticles can been written as ${\rm{\Delta }}={{\rm{\Delta }}}_{D}\,\sin \left(2{\theta }_{S}\right)$ and ${\rm{\Delta }}={{\rm{\Delta }}}_{D}\,\sin \left[2\left(\pi -{\theta }_{S}\right)\right]\,=-{{\rm{\Delta }}}_{D}\,\sin \left(2{\theta }_{S}\right),$ respectively. The signs of the pairing potential for the incident particles and its reflected particles are obviously opposite. This results in an interference effect between them, thus forming the zero-energy ABS. This zero-energy ABS leads to the ZBCP [24]. For NM/I/FM/${d}_{{x}^{2}-{y}^{2}}+is$ -wave superconducting structures, as shown in figure 1(a), when $\eta =\displaystyle \frac{{{\rm{\Delta }}}_{s}}{{{\rm{\Delta }}}_{D}}\ne 0,$ the ZBCP splits into two high-energy conductance peaks. With the increase in $\eta ,$ that is, with the enhancement of the s-wave subcomponent, the amplitude of the splitting peaks decreases and the distance between the peaks increases. It is worth noting that the position of the two peaks appear at exactly $\displaystyle \frac{eV}{{{\rm{\Delta }}}_{0}}=\pm \displaystyle \frac{{{\rm{\Delta }}}_{s}}{{{\rm{\Delta }}}_{D}}.$ Our result includes the experimental phenomenon in [25]. For NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave superconducting structures, as shown in figure 1(b), when $\eta =\displaystyle \frac{{{\rm{\Delta }}}_{d}}{{{\rm{\Delta }}}_{D}}\ne 0,$ the ZBCP still exists. At the same time, there are also high-energy conductance peaks at $\displaystyle \frac{eV}{{{\rm{\Delta }}}_{0}}=\pm \displaystyle \frac{{{\rm{\Delta }}}_{d}}{{{\rm{\Delta }}}_{D}},$ but the values of the peaks are smaller than those of the NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave SC junction tunnel spectrum. Unlike the NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave SC tunnel junction, with the increase in $\eta ,$ that is, with the enhancement of the ${d}_{xy}$ -wave component, the value of the ZBCP becomes smaller and smaller, while the value of the two non-zero-bias conductance peaks becomes larger and larger. We explain all the different behaviors of the tunnel spectrum caused by s- and ${d}_{xy}$ -wave subcomponents as follows. The induced s-wave component breaks the symmetry of time inversion, blocks the transport of the quasiparticles and causes the zero-energy ABS to no longer be stable. Thus, the energy level of ABS shifts from zero to $eV=\pm \displaystyle \frac{{{\rm{\Delta }}}_{s}}{{{\rm{\Delta }}}_{D}}{{\rm{\Delta }}}_{0}$ and the ZBCP splits accordingly into two conductance peaks. For the induced ${d}_{xy}$ -wave component, equation (1) shows that when $\eta =\displaystyle \frac{{{\rm{\Delta }}}_{s}}{{{\rm{\Delta }}}_{D}}\left(\displaystyle \frac{{{\rm{\Delta }}}_{d}}{{{\rm{\Delta }}}_{D}}\right)=0$ and $\alpha =0.25\pi ,$ the same as for the ${d}_{{x}^{2}-{y}^{2}}$ -wave, signs of the pairing potential for the incident particles and its reflected particles are opposite. Therefore, although it also breaks the symmetry of the time inversion, the zero-energy ABS still exists, and correspondingly, the ZBCP also exists. 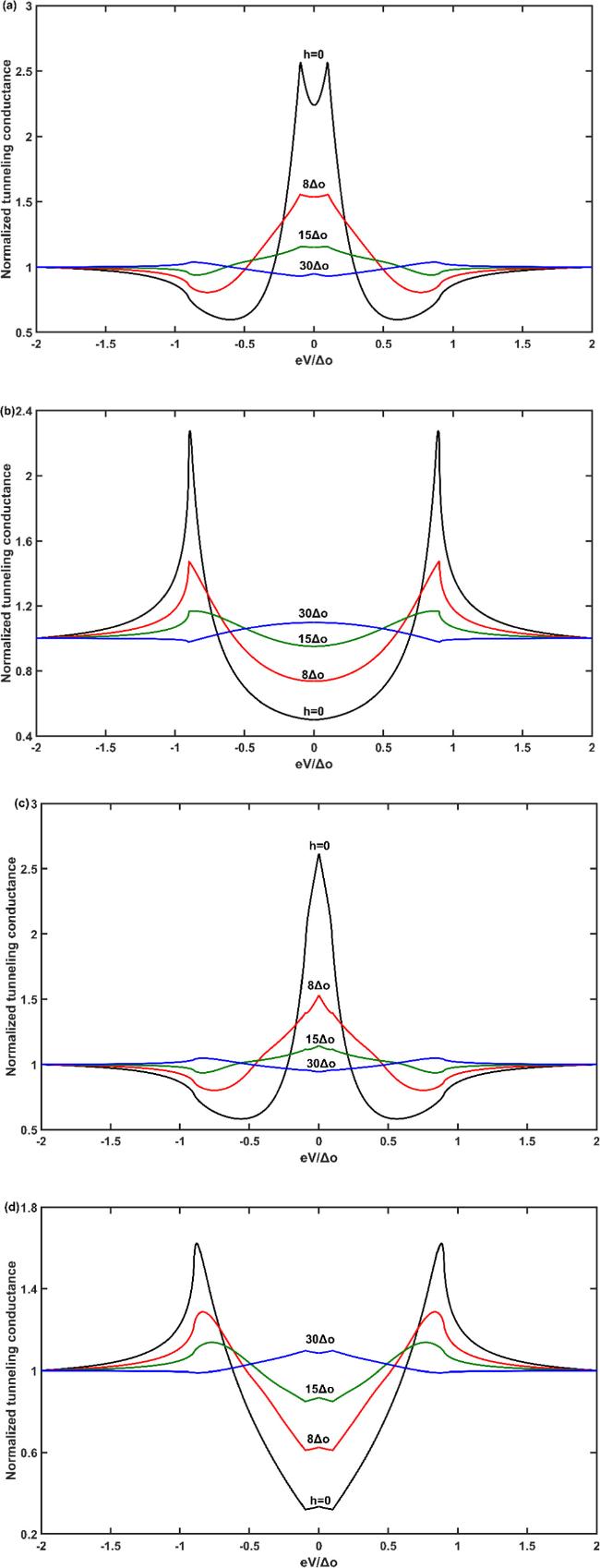It should be mentioned that although we take L = 5 nm here, it is calculated that the length L of ferromagnetic metal does not affect the splitting behavior caused by the s-wave subcomponent. The above results of the tunnel spectrum of NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave and NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave SC tunnel structures can be used to experimentally distinguish ${d}_{{x}^{2}-{y}^{2}}$ -wave from the mixed wave ${d}_{{x}^{2}-{y}^{2}}+is$ or ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy},$ and also to determine whether the TRSB is caused by subdominant pair potential s-wave or ${d}_{xy}$ -wave.

Next, the influence of the proximity effect on the tunneling conductance spectrum is discussed. The results are given in figure 2, where (a) and (b) plot the case of ${d}_{{x}^{2}-{y}^{2}}+is$ -wave, while (c) and (d) plot the case of ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave. In addition, figures 2(a) and (c) show the case when the TRSB effect is weak, where we take $\eta =\displaystyle \frac{1}{9}.$ Figures 2(b) and (d) show the case when the TRSB effect is strong, and we take $\eta =9.$ It can be seen from the four figures that with the increase in exchange energy denoted by h in the ferromagnetic metal layer, the shape of the tunnel spectral line is reversed. This means that no matter whether the TRSB effect is strong or weak, both NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave and NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave SC tunnel junctions change from ‘0 state’ to ‘π state’ with the increase in h. According to our calculation, as the thickness of the FM layer increases, the tunnel spectral lines of the two tunnel junctions will likewise exhibit a similar inversion phenomenon. Comparing figures 2(a) with (b), and (c) with (d), it can be seen that when h is small, the effect of TRSB on the shape of tunnel spectral lines is very obvious. With the increase in h, the overall fluctuation of spectral lines decreases. From a physical point of view, these behaviors can be explained as follows. When h is very small, due to the proximity effect, the superconducting state has great influence on the quasiparticle density of the FM, and the spectral lines of the tunnel are typical of NM/SC tunnel junctions. For example, when the s-wave component is dominant, the tunnel spectrum presents a typical zero-bias conductance dip (ZBCD), as shown in figure 2(b); when the ${d}_{{x}^{2}-{y}^{2}}$ -wave component dominates, the tunnel spectrum presents a typical ZBCP, as shown in figure 2(c). A large value of h results in a significant difference in wave vectors between up-spin and down-spin particles in FM, which in turn leads to the state transition of the tunnel junction. Comparing figures 2(a) with (c), and (b) with (d), one finds that the conductance spectrum of NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave SC tunnel junction is different from that of NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave SC tunnel junction due to the difference in the nature of the two types of TRSB. It is interesting that, as can be seen from figures 1(a) and 2(a), for the NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave SC tunnel junction, both the effect of TRSB and the exchange energy in FM can cause the splitting of the ZBCP. However, the splitting of the two effects is different. The position of the splitting peak caused by the TRSB state changes with the proportion of the s-wave component, while the splitting peak caused by h only was in a small energy range near the ZBCP.

Finally, the effect of tunneling quasiparticle lifetime on the conductance spectrum is shown in figure 3, where the normalized tunneling conductance varies with the bias voltage for different quasiparticle lifetime parameter ${\rm{\Gamma }}=\displaystyle \frac{\hslash }{\tau }$ is plotted. In [30], it is considered that inelastic scattering results in the shortening of the lifetime of quasiparticles near the NM/SC interface and found that when the values of ${\rm{\Gamma }}$ are in the range $5-12\,\mathrm{meV},$ the theory is in good agreement with the experimental results. For ${d}_{{x}^{2}-{y}^{2}}+is$ -wave SC, the value of ${{\rm{\Delta }}}_{0}$ in the experiment is generally $10-30\,\mathrm{meV}$ [25–27]. Based on the above experiments, we think it is reasonable to set the value range of ${\rm{\Gamma }}$ to be $0-2{{\rm{\Delta }}}_{0}$ for the system we studied. Figures 3(a) and (b) give the results for NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave SC tunnel junctions. Figure 3(a) shows the case of ${d}_{{x}^{2}-{y}^{2}}$ -wave dominance with ${{\rm{\Delta }}}_{D}=0.9{{\rm{\Delta }}}_{0}$ and ${{\rm{\Delta }}}_{s}=0.1{{\rm{\Delta }}}_{0}$ taken. One finds that when ${\rm{\Gamma }}=0,$ that is, without considering the finite lifetime of the quasiparticles, the splitting of the tip of the ZBCP is obtained. When the quasiparticle lifetime is considered, the splitting disappears. With the continuous increase in ${\rm{\Gamma }},$ that is, with the continuous decrease in quasiparticle lifetime, the ZBCP first gradually decreases to ZBCD, and then rises until it becomes a smooth line. Figure 3(b) plots the case of s-wave dominance, in which ${{\rm{\Delta }}}_{D}=0.1{{\rm{\Delta }}}_{0}$ and ${{\rm{\Delta }}}_{s}=0.9{{\rm{\Delta }}}_{0}$ are taken. From this, one can see that with the continuous decrease in quasiparticle lifetime, the ZBCD first gradually evolves into a broad ZBCP, and then the ZBCP gradually decreases, and finally also becomes a smooth line. These changes in the tunnel spectra show that the length of the quasiparticle lifetime has a significant effect on the conductance characteristics caused by the TRSB and proximity effects. To see more clearly the effect of continuous changes of the quasiparticle lifetime on the tunnel spectral lines, we draw a 3D diagram for NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave SC tunnel junction, as shown in figures 3(c) and (d). From figure 3(c), it can be seen that for the case of ${d}_{{x}^{2}-{y}^{2}}$ -wave dominance, as ${\rm{\Gamma }}$ increases, the ZBCP gradually decreases to a ZBCD, and then the ZBCD gradually rises until it forms a smooth surface. For the case of ${d}_{xy}$ -wave dominance, the small ZBCP at the bottom of the ZBCD is first smoothed out, then the ZBCD is gradually lifted to a flat peak, and finally flattened to a smooth surface. These results reveal that the shorter the lifetime of the transporting particles, the weaker the proximity effect, which in turn leads to the disappearance of features such as dips and peaks in the tunneling conductance spectra. Since the finiteness of the quasiparticle lifetime is essentially due to the inelastic scattering in the superconducting tunnel junction [26], we consider that the too large inelastic scattering at the interface of the tunnel junction may be the reason that the splitting of the ZBCP was not observed in some previous experiments. Therefore, it is suggested that in order to better realize the results of this paper in the experiment, the quality of tunnel junctions should be improved as much as possible to make it as clean as possible.

In this paper, the effects of TRSB, proximity effect and finiteness of quasiparticle lifetime on the transporting properties of NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave and NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}$ -wave SC tunnel structures are systematically investigated. For the conductance spectra of both types of tunnel junctions, there are conductance peaks at $\displaystyle \frac{eV}{{{\rm{\Delta }}}_{0}}=\pm \displaystyle \frac{{{\rm{\Delta }}}_{s}}{{{\rm{\Delta }}}_{D}}\left(\displaystyle \frac{{{\rm{\Delta }}}_{d}}{{{\rm{\Delta }}}_{D}}\right).$ This splitting is different from that caused by the exchange energy in FM and can be used to measure the ratio of the subdominant s- and ${d}_{xy}$ -wave component to the dominant ${d}_{{x}^{2}-{y}^{2}}$ -wave in the mixed wave ${d}_{{x}^{2}-{y}^{2}}+is$ and ${d}_{{x}^{2}-{y}^{2}}+i{d}_{xy}.$ With the increase in ferromagnetic exchange energy, the shape of the tunneling conductance spectrum is completely reversed, which reveals that the proximity effect will cause the investigated tunnel junctions to transform from ‘0 state’ to ‘π state’. The shorter the lifetime of the tunneling particles in the tunnel junction, the weaker the proximity effect, and eventually the dips and peaks in the tunnel spectrum are smoothed out. For NM/I/FM/ ${d}_{{x}^{2}-{y}^{2}}+is$ -wave SC tunnel structures, if the quasiparticle lifetime is long enough, the splitting of the ZBCP can be observed experimentally. We are confident that the analysis in this paper will serve as a guide for future experiments during which the relevant conclusions can be confirmed.

This study is supported by the Fundamental Research Funds for the Central Universities (Grant Nos. 23CX03016A and 24CX030009A).