1. Introduction
Quantized vortices are topological defects generated in superfluids, endowing them with angular momentum and playing a fundamental role in both quantum and classical turbulence. The dynamics of these vortices has always been a significant research focus in the field of superfluidity. Although quantized vortices were first confirmed in liquid helium superfluids, the vortex size in this medium is extremely small, making visualization difficult. Later, quantized vortices were directly observed in gaseous Bose–Einstein condensates (BECs), where their size is thousands of times larger than those in liquid helium. This has made gaseous BECs an ideal platform for studying quantized vortices and quantum turbulence. The circulation around a vortex core corresponds to an integer multiple of 2π, with the integer n being the quantum number of the vortex, known as the winding number. The vortex energy scales with the square of its winding number. Therefore, a singly quantized vortex (n = 1) has the minimum energy and is the most stable. In contrast, vortices with winding numbers n ≥ 2 have a higher energy and are unstable, tending to split into n singly quantized vortices, a process central to the emergence and comprehension of quantum turbulence. This splitting dynamics provides insights into vortex behavior under rapid background velocity changes on the scale of the vortex core. The splitting dynamics of the multiply quantized vortices has been thoroughly investigated [1–41], revealing that vortices with a winding number n ≥ 2 typically possess splitting instabilities characterized by rotational symmetries of p = 2, ⋯, 2(n − 1).
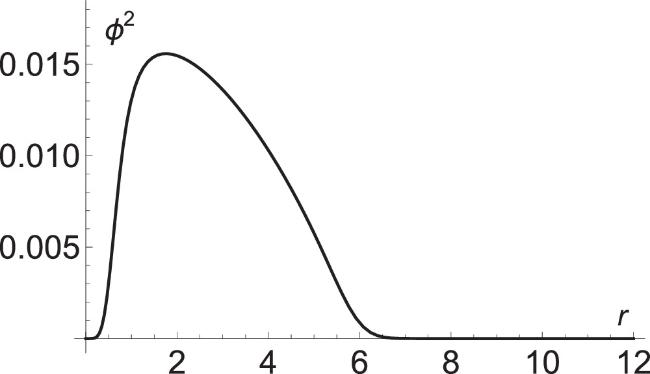
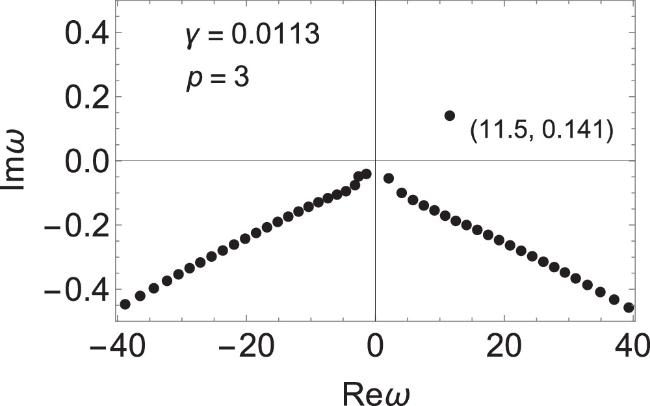
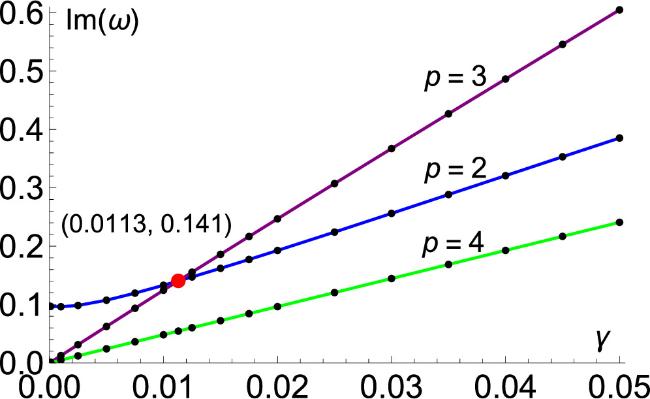
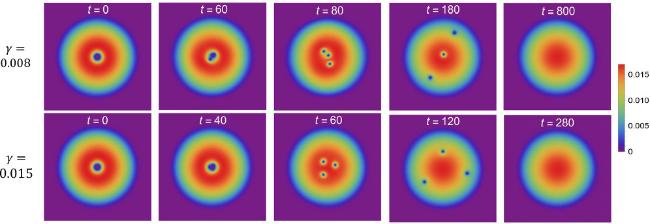
Techniques for generating quantized vortices with a high winding number in gaseous BECs include topological phase [42–44], the use of Laguerre–Gaussian beams [45] and spiraling laser beams around an obstacle [46]. Multiply quantized vortices have been created in the laboratory with winding numbers as high as 11 [46]. Of particular interest are triply quantized (n = 3) vortices [1, 6, 7, 12, 13, 16, 18, 24, 31, 32, 41], the dynamics of which are neither as trivial as those of doubly quantized (n = 2) vortices nor as complex as those of multiply quantized (n ≥ 4) vortices. 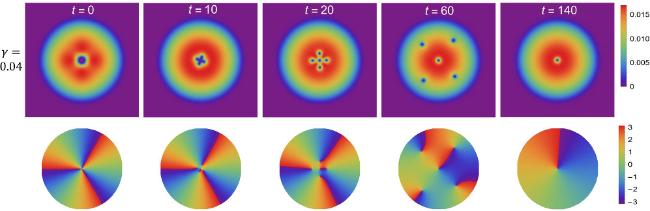The n = 3 vortices are prone to instabilities that result in a split with p = 2-, 3- or 4-fold rotational symmetries, corresponding to three distinct splitting patterns. According to the theoretical argument of energy and angular momentum [7, 13], the configuration of the p = 2 splitting pattern consists of three n = 1 vortices in a linear arrangement, whereas the p = 3 splitting pattern forms a triangular configuration of n = 1 vortices while the p = 4 splitting pattern features four n = 1 vortices orbiting a central n = −1 vortex. These splitting dynamics of n = 3 quantized vortices are numerically simulated using the zero temperature Gross–Pitaevskii equation (GPE). Only the p = 2 splitting pattern was observed in [16, 32] under random perturbations, while the p = 3 and p = 4 splitting patterns were observed in [24] for specific chemical potentials and confinement potentials. A subsequent question that arises is: what governs the specific splitting pattern of the triply quantized vortices? It is important to acknowledge that the influence of finite temperature, originating from the surrounding environment acting as a thermal bath, is inevitable. The splitting patterns and dynamical transitions of quadruply quantized vortices at finite temperature were investigated in [22] by holographic duality. Interestingly, the splitting patterns were found to be determined by temperature. With increasing temperature the splitting pattern changes, transitioning from the p = 2 mode to the p = 3 mode, and subsequently from the p = 3 mode to the p = 4 mode. Inspired by this work, we utilize the dissipative GPE and explore the impact of finite temperature on the splitting dynamics of triply quantized vortices within oblate-shaped BECs, which are effectively considered as two-dimensional systems.
The structure of this paper is as follows. Section 2 delves into linear analysis of the stability of triply quantized vortices. Section 3 presents comprehensive numerical simulations exploring the splitting dynamics of these vortices. Finally, section 4 provides the conclusions and discusses the findings.
2. Triply quantized vortices and their linear instability
In the context of a BEC characterized by an oblate shape, the dynamics of the system can be effectively captured by a two-dimensional dissipative GPE [47–53]
$\begin{eqnarray}{\rm{i}}{\hslash }\displaystyle \frac{\partial \psi }{\partial t}=(1-{\rm{i}}\gamma )\left(-\displaystyle \frac{{{\hslash }}^{2}}{2m}{{\rm{\nabla }}}^{2}\psi +g| \psi {| }^{2}\psi -\mu \psi +V\psi \right),\end{eqnarray}$
where γ > 0 is a dissipative parameter which is supposed to increase monotonically with temperature. The wavefunction $\psi (\vec{x},t)$ serves as the complex order parameter that encapsulates the quantum state of N bosons, each with mass m. The interaction strength between these bosons is quantified by the parameter g. The system's chemical potential is represented by μ. For the purpose of this study, the bosons are confined within a harmonic potential, denoted as V $\begin{eqnarray}V=\displaystyle \frac{1}{2}m{\omega }_{0}^{2}({x}^{2}+{y}^{2}).\end{eqnarray}$
Implementing the following scaling change $\begin{eqnarray}\begin{array}{rcl}t & = & \displaystyle \frac{t^{\prime} }{{\omega }_{0}},\vec{x}=\sqrt{\displaystyle \frac{{\hslash }}{m{\omega }_{0}}}\vec{x^{\prime} },\mu ={\hslash }{\omega }_{0}\mu ^{\prime} ,\\ \psi & = & \sqrt{\displaystyle \frac{m{\omega }_{0}N}{{\hslash }}}\psi ^{\prime} ,g=\displaystyle \frac{{{\hslash }}^{2}}{{mN}}g^{\prime} ,\end{array}\end{eqnarray}$
the dissipative GPE becomes $\begin{eqnarray}{\rm{i}}\displaystyle \frac{\partial \psi }{\partial t}=(1-{\rm{i}}\gamma )\left(-\displaystyle \frac{1}{2}{{\rm{\nabla }}}^{2}\psi +g| \psi {| }^{2}\psi -\mu \psi +\displaystyle \frac{1}{2}({x}^{2}+{y}^{2})\psi \right).\end{eqnarray}$
Note that we have dropped the primes to streamline the notation. Additionally, the normalization condition for the wavefunction is ∫∣$\Psi$∣2dxdy = 1.To see the effect of the dissipative parameter γ, one can obtain
$\begin{eqnarray}{\partial }_{t}F=-\displaystyle \frac{2\gamma }{1+{\gamma }^{2}}\int {\rm{d}}x{\rm{d}}y| {\partial }_{t}\psi {| }^{2},\end{eqnarray}$
where F is the free energy functional of the system $\begin{eqnarray}F[\psi ]=\int {\rm{d}}x{\rm{d}}y\left(\displaystyle \frac{1}{2}| {\rm{\nabla }}\psi {| }^{2}+\displaystyle \frac{g}{2}| \psi {| }^{4}-\mu | \psi {| }^{2}+\displaystyle \frac{1}{2}({x}^{2}+{y}^{2})| \psi {| }^{2}\right).\end{eqnarray}$
The dissipation of free energy increases with the dissipation strength for 0 < γ < 1.A vortex with a quantized circulation exhibits rotational invariance, and in polar coordinates its wavefunction is given by $\Psi$(r, θ) = φ(r)einθ, with n denoting the winding number of the vortex. The state of such a vortex can be determined by resolving the following dynamical equation:
$\begin{eqnarray}\displaystyle \frac{{{\rm{d}}}^{2}\phi }{2{\rm{d}}{r}^{2}}+\displaystyle \frac{{\rm{d}}\phi }{2r{\rm{d}}r}-\displaystyle \frac{{n}^{2}}{2{r}^{2}}\phi -g| \phi {| }^{2}\phi +\mu \phi -\displaystyle \frac{1}{2}{r}^{2}\phi =0.\end{eqnarray}$
At the center r = 0 and boundary r = R of the vortex (where R denotes a sufficiently large radius), the specified boundary conditions are as follows: $\begin{eqnarray}\phi {\Space{0ex}{3.25ex}{0ex}| }_{r=0}=0,\,\,\displaystyle \frac{{\rm{d}}\phi }{{\rm{d}}r}{\Space{0ex}{3.25ex}{0ex}| }_{r=R}=0.\end{eqnarray}$
Fixing the winding number at n = 3 and employing the pseudo-spectral technique with 120 Chebyshev polynomials along the radial direction, we arrive at the targeted configuration for a triply quantized vortex, depicted in figure 1. In line with the experimental parameters reported in references [10, 20, 34, 35, 54, 55], our analysis centers on an interaction strength of g = 1000. The normalization condition for the order parameter, which states that $2\pi {\int }_{0}^{\infty }| \phi {| }^{2}r{\rm{d}}r=1$ , leads to the determination of the chemical potential as μ = 18.651.
Figure 1. The configuration for a triply quantized vortex at an interaction strength of g = 1000. |
Next we will investigate the stability characteristics of the previously obtained vortices. Given that the vortex backgrounds exhibit both temporal translation and rotational symmetries, we can construct the linear perturbation of the wavefunction $\Psi$(r, θ) as follows:
$\begin{eqnarray}\psi ={{\rm{e}}}^{{\rm{i}}n\theta }\left(\phi (r)+\delta {\phi }_{1}(r){{\rm{e}}}^{-{\rm{i}}\omega t+{\rm{i}}p\theta }+\delta {\phi }_{2}^{* }(r){{\rm{e}}}^{{\rm{i}}{\omega }^{* }t-{\rm{i}}p\theta }\right),\end{eqnarray}$
where ω is the eigenfrequency and p is the azimuthal number. By linearizing the dissipative GPE, we derive the Bogoliubov equation $\begin{eqnarray}\left[\begin{array}{cc}{h}_{+} & g{\phi }^{2}\\ -g{\phi }^{2} & -{h}_{-}\end{array}\right]\left[\begin{array}{c}\delta {\phi }_{1}\\ \delta {\phi }_{2}\end{array}\right]=0,\end{eqnarray}$
with $\begin{eqnarray}\begin{array}{rcl}{h}_{\pm } & = & -\displaystyle \frac{{{\rm{d}}}^{2}}{2{\rm{d}}{r}^{2}}-\displaystyle \frac{{\rm{d}}}{2r{\rm{d}}r}+2g{\phi }^{2}-\mu \mp \displaystyle \frac{\omega }{1\mp {\rm{i}}\gamma }\\ & & +\,\displaystyle \frac{{\left(n\pm p\right)}^{2}}{2{r}^{2}}+\displaystyle \frac{1}{2}{r}^{2}.\end{array}\end{eqnarray}$
At the points r = 0 and r = R, the specified boundary conditions of δφ1,2 are set as follows: $\begin{eqnarray}\delta {\phi }_{\mathrm{1,2}}{\Space{0ex}{3.25ex}{0ex}| }_{r=0}=0,\,\,\displaystyle \frac{{\rm{d}}\delta {\phi }_{\mathrm{1,2}}}{{\rm{d}}r}{\Space{0ex}{3.25ex}{0ex}| }_{r=R}=0.\end{eqnarray}$
The eigenfrequency ω(g, γ, p) corresponding to the excitation modes is computed by numerically addressing the eigenvalue issue. Figure 2 illustrates the spectrum of the lower eigenfrequencies (ω) under the parameters g = 1000, γ = 0.0113 and p = 3. Notably, one eigenfrequency (ω = 11.5 + 0.141i) exhibits a positive imaginary part, signaling the instability of the triply quantized vortex within the p = 3 case.
Figure 2. The spectrum of the lower eigenfrequencies (ω) of the triply quantized vortex under the parameters g = 1000, γ = 0.0113 and p = 3. |
Figure 3 displays the variation trend of the imaginary part of the dominant mode with the dissipation parameter γ ranging from 0.000 01 to 0.05 at g = 1000. From the figure the following can be observed. First, the existence of three unstable modes, p = 2, 3 and 4, is confirmed. Second, it is noted that the larger the dissipation strength, the greater the imaginary part of the dominant mode. In particular, in the case of p = 2, $\mathrm{Im}(\omega )$ starts from a non-zero value. For the cases of p = 3 and p = 4, $\mathrm{Im}(\omega )$ starts from zero. Therefore, in a non-dissipative superfluid system the only instability of the triply quantized vortex comes from the p = 2 case. Third, when γ ≲ 0.0113 the most unstable mode corresponds to the p = 2 mode; when γ ≳ 0.0113 the most unstable mode shifts to the p = 3 mode. This result indicates a dynamical transition of the unstable mode from the p = 2 mode to the p = 3 mode at γ = 0.0113. Fourth, the p = 4 mode is never the dominant one throughout the entire range of dissipation parameters.
Figure 3. The variation trend of the imaginary part of the dominant mode with the dissipation parameter γ ranging from 0.000 01 to 0.05 at g = 1000. |
3. Numerical simulation and splitting dynamics of triply quantized vortices
Next we will illustrate the significant dynamical transition of the unstable mode from p = 2 to p = 3 through real-time simulations of the splitting processes in triply quantized vortex systems. The starting conditions are established by introducing perturbations to $\Psi$ based on the previously obtained stationary configurations, as outlined below
$\begin{eqnarray}\psi (r,\theta )={{\rm{e}}}^{{\rm{i}}3\theta }\phi (r)(1+\displaystyle \sum _{p=1}^{Q}(\alpha (p){{\rm{e}}}^{-{\rm{i}}p\theta }+\beta (p){{\rm{e}}}^{{\rm{i}}p\theta })).\end{eqnarray}$
In this setup, α(p) and β(p) are irrelevant and arbitrarily selected minor constants of the order of 10−4, while Q is a random integer ranging from 3 to 20, which does not affect the outcome of the numerical simulations. To enhance the precision of these simulations, we opt to utilize rectangular coordinates instead of polar coordinates. Consequently, the initial dataset in the rectangular coordinate system is expressed as $\Psi$(t = 0, x, y).The initial dataset generates the vortex in the central area of the system, as shown in figure 4. Furthermore, the data approach zero at the edges of the square domain, allowing for the application of periodic boundary conditions in our numerical computations. Specifically, our simulations utilize 159 Fourier modes for both the x and y directions (resulting in a 159 × 159 grid within a 16 × 16 simulation area), along with the fourth-order Runge–Kutta algorithm for time evolution with a time step of Δt = 0.002. Throughout the simulation, the total number of ultracold atoms is conserved (such that ∫∣$\Psi$∣2dxdy = 1), as detailed in [56]. We have verified that the findings are independent of grid size and time step by performing one simulation on a 319 × 319 grid and Δt = 0.001 which gave identical results.
Figure 4. Visual representations of the condensate density during the splitting processes of triply quantized vortices subjected to random perturbations at g = 1000. Varied vortex splitting patterns are identified corresponding to distinct dissipation levels γ = 0.008 and 0.015 from top to bottom. |
Figure 4 illustrates the splitting dynamics of triply quantized vortices under random perturbations at g = 1000, for γ = 0.008 and 0.015. The splitting dynamics exhibit distinct patterns of p-fold rotational symmetry corresponding to the different dissipation levels. At a lower dissipation rate of γ = 0.008, which is less than 0.0113, the p = 2 splitting pattern is dominant. Conversely, at a higher dissipation rate of γ = 0.015, exceeding 0.0113, the p = 3 splitting pattern becomes dominant. This variation in splitting patterns with dissipation strength aligns with the linear perturbation analysis presented previously. As far as we know, only the p = 2 splitting pattern has been observed under random perturbation conditions in previous studies [16, 32, 41]. The p = 3 and p = 4 splitting patterns were only observed in [24] under conditions of specific chemical potentials and confinement potentials. Our findings suggest that the p = 3 splitting pattern can emerge naturally in BECs by enhancing the dissipation strength, or equivalently by increasing the system's temperature.
Taking into account that the p = 4 unstable mode never dominates, to witness the p = 4 splitting pattern in our dissipative GPE model we can no longer use random perturbation; instead, we need to adopt the p = 4 type perturbation, i.e.
$\begin{eqnarray}\psi (r,\theta )={{\rm{e}}}^{{\rm{i}}3\theta }\phi (r)(1+\alpha {{\rm{e}}}^{-{\rm{i}}4\theta }+\beta {{\rm{e}}}^{{\rm{i}}4\theta }),\end{eqnarray}$
with α and β being minor coefficients of the order of 10−2. The ensuing splitting processes are depicted in figure 5. It is evident that the p = 4 splitting pattern yields four n = 1 quantized vortices orbiting a central n = −1 vortex.
Figure 5. Visual representations of the condensate density and phase during the splitting processes of triply quantized vortices, subjected to p = 4 type perturbation at γ = 0.04 and g = 1000. |
To see the evolution dynamics of the system, we study the evolution of free energy (equation (6 )) which decreases with time in figure 6. Notably, the study reveals that the case of a p = 4 splitting pattern results in a metastable state with one anti-vortex remaining in the center of the system as the free energy does not change with time in the late stage of evolution.
Figure 6. Evolution of free energy for varying dissipation coefficients γ = 0.008, 0.015 and 0.04. |
4. Conclusion and discussion
The effect of finite temperature (dissipation strength) on the splitting dynamics of n = 3 vortices is investigated using the dissipative GPE. Firstly, the n = 3 vortex configuration is obtained by solving the equation of motion numerically. Secondly, the stability characteristics of these vortices are probed by examining the excitation modes, derived from linear perturbation theory. A key finding is the dynamical transition of the most unstable mode from p = 2 at lower dissipation levels to p = 3 at higher dissipation levels. Thirdly, we performed numerical simulations of the vortex splitting process. At lower dissipation levels the p = 2 splitting pattern is dominant, whereas at higher dissipation levels the p = 3 splitting pattern becomes dominant. The outcomes of the simulations align with the findings of perturbation analysis. Our findings elucidate why the p = 2 splitting pattern, observed at zero temperature in [16, 32], is more readily observable compared with the p = 3 splitting pattern, which typically requires finite temperature or specific chemical and confinement potentials, as seen in [24]. We suggest that a straightforward method to witness the p = 3 splitting pattern is by raising the system's temperature. What’s more, we demonstrate the p = 4 splitting pattern under p = 4 type perturbation. With significant experimental progress in superfluids [57, 58], the dynamics of quantized vortices at finite temperatures has become amenable to experimental manipulation. Consequently, our predictions are expected to be verifiable in experiments.
We have studied the dissipative GPE written as follows [52]:
$\begin{eqnarray}({\rm{i}}-\gamma ){\hslash }\displaystyle \frac{\partial \psi }{\partial t}=\left(-\displaystyle \frac{{{\hslash }}^{2}}{2m}{{\rm{\nabla }}}^{2}\psi +g| \psi {| }^{2}\psi -\mu \psi +V\psi \right).\end{eqnarray}$
It should be mentioned that the result would not change when γ ≤ 0.05. Future research directions include other interaction strengths, other multiply quantized vortices and three-dimensional superfluid systems.Acknowledgments
Funding for this research was provided by the Guangdong Basic and Applied Basic Research Foundation of China (Grant Nos. 2024A1515012552, 2022A1515011938, 2022A1515012425) and the National Natural Science Foundation of China (Grant No. 12005088). SL is grateful for the support received from Lingnan Normal University (Grant Nos. YL20200203, ZL1930). The manuscript's quality was greatly enhanced by the valuable feedback from the reviewers and editor, to whom the authors extend their heartfelt thanks.