1. Introduction
As a model of relativistic field theory, the massive Thirring model (MTM) system was first proposed by Thirring [1]. The two-dimensional MTM is written in light cone coordinates [2]
$\begin{eqnarray}{\rm{i}}{u}_{X}+v+u| v{| }^{2}=0,\end{eqnarray}$
$\begin{eqnarray}{\rm{i}}{v}_{T}+u+v| u{| }^{2}=0,\end{eqnarray}$
where u and v are complex-valued functions of X and T. Compared with the massless Thirring model, such a system is said to be massive due to the existence of the linear terms u and v [1]. System (1) can depict the self-interaction between vectors in a Dirac field within (1+1) dimensions and serves as a simplified version of the Dirac–Maxwell system [3]. The integrability of system (1) has been proved in the sense of Bäcklund transformation and infinite conserved quantities [4, 5]. The N-soliton solutions under nonvanishing background were given by the reduction from the generic system describing integrable relativistic massive fields [6, 7]. The algebro-geometric solutions have also been studied in the literature [8, 9]. In addition, the rogue wave solutions were presented by using the Darboux transformation [10, 11] and KP hierarchy reduction method [12]. Further, [13] established the transformation between the Fokas–Lenells equation and system (1) whose soliton solutions were then obtained indirectly. The bright/dark-soliton and breather solutions in terms of Gram determinants were derived via the Hirota's bilinear and KP hierarchy reduction technique [14].Noted that with the transformation x = X − T and t = X + T, system (1) can also be written in laboratory coordinates
$\begin{eqnarray}{\rm{i}}\left({u}_{t}+{u}_{x}\right)+v+u| v{| }^{2}=0,\end{eqnarray}$
$\begin{eqnarray}{\rm{i}}\left({v}_{t}-{v}_{x}\right)+u+v| u{| }^{2}=0,\end{eqnarray}$
which has significant physical implications for describing the pulse propagation in nonlinear optics such as Bragg gratings [15–17], deep water waves in oceans with a periodic bottom terrain [18, 19] and superpositions of two hyperfine Zeeman sublevels in atomic Bose–Einstein condensates [20]. Kuznetsov and Mikhailov first solved this system by the inverse scattering transform (IST) and the Lax pair as well as infinite conserved quantities were also found [21, 22]. Reference [23] developed the IST for system (2) and constructed the Riemann–Hilbert (RH) problem with the scattering coefficients having no zeros. In [24], the semi-discrete MTM was proposed and the soliton solutions were derived through the Darboux transformation method. The long-time behaviors of the solutions for system (2) were established in weighted Sobolev spaces and soliton resolution as well as multi-soliton asymptotic stability were further analyzed [25, 26]. More recently, the exact solutions describing dynamics of two algebraic solitons were studied in [27].It is known that system (2) admits the following Lax pair [21]
$\begin{eqnarray}{{\rm{\Phi }}}_{x}\left(x,t;\lambda \right)=L\left(x,t;\lambda \right){\rm{\Phi }}\left(x,t;\lambda \right),\end{eqnarray}$
$\begin{eqnarray}{{\rm{\Phi }}}_{t}\left(x,t;\lambda \right)=A\left(x,t;\lambda \right){\rm{\Phi }}\left(x,t;\lambda \right),\end{eqnarray}$
with $\begin{eqnarray}\begin{array}{l}\,L\left(x,t;\lambda \right)=\frac{{\rm{i}}}{4}\left(| u{| }^{2}-| v{| }^{2}\right){\sigma }_{3}-\frac{{\rm{i}}\lambda }{2}V\\ \quad +\,\frac{{\rm{i}}}{2\lambda }U+\frac{{\rm{i}}}{4}\left({\lambda }^{2}-\frac{1}{{\lambda }^{2}}\right){\sigma }_{3},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{l}\,A\left(x,t;\lambda \right)=-\frac{{\rm{i}}}{4}\left(| u{| }^{2}+\,| v{| }^{2}\right){\sigma }_{3}-\frac{{\rm{i}}\lambda }{2}V-\frac{{\rm{i}}}{2\lambda }U\\ \,+\,\frac{{\rm{i}}}{4}\left({\lambda }^{2}+\frac{1}{{\lambda }^{2}}\right){\sigma }_{3},\end{array}\end{eqnarray}$
and $\begin{eqnarray*}U=\left(\begin{array}{cc}0 & \overline{u}\\ u & 0\end{array}\right),\quad V=\left(\begin{array}{cc}0 & \overline{v}\\ v & 0\end{array}\right),\quad {\sigma }_{3}=\left(\begin{array}{cc}1 & 0\\ 0 & -1\end{array}\right),\end{eqnarray*}$
where Φ is a matrix function, the bar '–' denotes the complex conjugation. The compatibility condition ${L}_{t}-{A}_{x}+\left[L,A\right]\,=0$ $\left(\left[L,A\right]:= LA-AL\right)$ can lead to system (2). In this paper, we focus on applying the RH method to the MTM system in laboratory coordinates (i.e., system (2)) with the scattering coefficients having simple zeros, deriving the N-soliton solutions directly from the original spectral problem and especially performing the asymptotic analysis on the soliton interactions as ∣t∣ → ∞.The structure of this paper is arranged as follows: In section 2 , we study the analyticity, symmetries and asymptotic behaviors of the Jost solutions and scattering matrices. In section 3 , we establish two RH problems, residue conditions, reconstruction formulas and trace formulas. In the reflectionless case, N-soliton solutions of system (2) are expressed explicitly. In section 4 , we discuss the propagation characteristics of one-soliton solutions and the interaction properties of two-soliton solutions. In particular, we derive the asymptotic soliton expressions at large ∣t∣ and discuss three types of two-soliton bounded states with certain parametric conditions. Finally, the conclusions are presented in section 5 .
2. Direct scattering
In this section, we will analyze the direct scattering of system (2) including the analyticity, symmetries and asymptotic behaviors of the Jost solutions and scattering matrices. Due to the existence of λ and λ−1 in Lax pair (3), the IST problem cannot be analyzed uniformly for large and small spectral parameters λ. In this paper, we separately consider the spectral problem (3) and its equivalent form obtained under the inversion transformation λ = 1/ω.
2.1. Direct scattering for λ
2.1.1. Lax pair, integral equations and analyticity of modified Jost solutions
As x → ± ∞, the asymptotic scattering problem of Lax pair (3) with the zero boundary conditions (i.e., u, v → 0 as x → ± ∞) reads
$\begin{eqnarray}{{\rm{\Phi }}}_{x}\left(x,t;\lambda \right)={L}_{\pm }\left(x,t;\lambda \right){\rm{\Phi }}\left(x,t;\lambda \right),\quad {L}_{\pm }\left(x,t;\lambda \right):= \frac{{\rm{i}}}{4}\left({\lambda }^{2}-\frac{1}{{\lambda }^{2}}\right){\sigma }_{3},\end{eqnarray}$
$\begin{eqnarray}{{\rm{\Phi }}}_{t}\left(x,t;\lambda \right)={A}_{\pm }\left(x,t;\lambda \right){\rm{\Phi }}\left(x,t;\lambda \right),\quad {A}_{\pm }\left(x,t;\lambda \right):= \frac{{\rm{i}}}{4}\left({\lambda }^{2}+\frac{1}{{\lambda }^{2}}\right){\sigma }_{3}.\end{eqnarray}$
Note that the fundamental matrix solution ${{\rm{\Phi }}}_{bg}\left(x,t;\lambda \right)$ of equations (5) can be given by
$\begin{eqnarray}{{\rm{\Phi }}}_{bg}\left(x,t;\lambda \right)={{\rm{e}}}^{{\rm{i}}\theta \left(x,t;\lambda \right){\sigma }_{3}},\quad \theta \left(x,t;\lambda \right)=\frac{1}{4}\left[\left({\lambda }^{2}-\frac{1}{{\lambda }^{2}}\right)x+\left({\lambda }^{2}+\frac{1}{{\lambda }^{2}}\right)t\right].\end{eqnarray}$
Thus, we seek the Jost solutions ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$ of Lax pair (3), which satisfy the following asymptotic conditions $\begin{eqnarray}{{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)\unicode{x0007E}{{\rm{e}}}^{{\rm{i}}\theta \left(x,t;\lambda \right){\sigma }_{3}},\quad x\to \pm \infty ,\end{eqnarray}$
where the subscripts ± correspond to x → ± ∞, respectively.Meanwhile, for the time evolution of ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$, we have the following statement.
(Time evolution) The Jost solutions ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$ satisfy Lax pair (3).
Because ${\rm{tr}}\left(L\right)=0$, Abel's identity tells us that ${\rm{\det }}{{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)=1$, which means that ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$ are the fundamental matrix solutions. With the zero curvature equation ${L}_{t}-{A}_{x}+\left[L,A\right]=0$, we can find that $\frac{{\rm{d}}}{{\rm{d}}t}{{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)-A{{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$ also satisfies Lax pair (
$\begin{eqnarray*}\frac{{\rm{d}}}{{\rm{d}}t}{{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)-A{{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)={G}_{\pm }\left(t;\lambda \right){{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right).\end{eqnarray*}$
Multiplying both sides by ${{\rm{e}}}^{-{\rm{i}}\theta \left(x,t;\lambda \right){\sigma }_{3}}$ and letting x → ± ∞, we immediately have ${G}_{\pm }\left(t;\lambda \right)=0$. As a result, the left-hand side equals to 0, that is, the Jost solutions ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$ satisfy Lax pair (To eliminate the exponential oscillations of Φ±, the modified Jost solution ${\mu }_{\pm }\left(x,t;\lambda \right)$ is introduced as 8 ) into equations (3), the modified Lax pair is written as:
$\begin{eqnarray}{\mu }_{\pm }\left(x,t;\lambda \right)={{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right){{\rm{e}}}^{-{\rm{i}}\theta \left(x,t;\lambda \right){\sigma }_{3}},\end{eqnarray}$
such that ${\mu }_{\pm }\left(x,t;\lambda \right)\unicode{x0007E}I$ as x → ± ∞, where I is a 2 × 2 identity matrix. Inserting equation ( $\begin{eqnarray}{\mu }_{\pm ,x}\left(x,t;\lambda \right)+\frac{{\rm{i}}}{4}\left({\lambda }^{2}-\frac{1}{{\lambda }^{2}}\right)\left[{\mu }_{\pm }\left(x,t;\lambda \right),{\sigma }_{3}\right]={L}_{1}\left(x,t;\lambda \right){\mu }_{\pm }\left(x,t;\lambda \right),\end{eqnarray}$
$\begin{eqnarray}{\mu }_{\pm ,t}\left(x,t;\lambda \right)+\frac{{\rm{i}}}{4}\left({\lambda }^{2}+\frac{1}{{\lambda }^{2}}\right)\left[{\mu }_{\pm }\left(x,t;\lambda \right),{\sigma }_{3}\right]={A}_{1}\left(x,t;\lambda \right){\mu }_{\pm }\left(x,t;\lambda \right),\end{eqnarray}$
where $\begin{eqnarray*}\begin{array}{rcl}{L}_{1}\left(x,t;\lambda \right): & = & \frac{{\rm{i}}}{4}\left({\left|u\right|}^{2}-{\left|v\right|}^{2}\right){\sigma }_{3}-\frac{{\rm{i}}\lambda }{2}V+\frac{{\rm{i}}}{2\lambda }U,\\ {A}_{1}\left(x,t;\lambda \right): & = & -\frac{{\rm{i}}}{4}\left({\left|u\right|}^{2}+{\left|v\right|}^{2}\right){\sigma }_{3}-\frac{{\rm{i}}\lambda }{2}V-\frac{{\rm{i}}}{2\lambda }U.\end{array}\end{eqnarray*}$
The behaviour of μ± as λ → 0 and $\left|\lambda \right|\to \infty $ has been studied in [23] via two matrix transformations which transform the modified spectral problem (9) denoted by $\left\{{\mu }_{\pm ,1},{\mu }_{\pm ,2}\right\}$ to two equivalent forms about the new normalized Jost functions $\left\{{m}_{\pm },{n}_{\pm }\right\}$ for small λ and $\left\{{\hat{m}}_{\pm },{\hat{n}}_{\pm }\right\}$ for large λ. They have proved rigorously that such two sets of new Jost functions about z := λ2 are analytic in ${{\mathbb{C}}}^{\pm }$ and continuous in ${{\mathbb{C}}}^{\pm }\cup {\mathbb{R}}$, given by lemma 5 in [23], where ${{\mathbb{C}}}^{\pm }$, respectively, corresponds to the upper and lower half-planes of the complex plane.
In the following, we will further derive the analyticity of the modified Jost functions $\left\{{\mu }_{\pm ,1},{\mu }_{\pm ,2}\right\}$. According to the relationships between the modified Jost functions and new ones given by equations (2.9) and (2.18) in [23], we have
$\begin{eqnarray}{\mu }_{\pm ,1}\left(x;\lambda \right)=\left(\begin{array}{cc}1 & 0\\ -\lambda u(x) & \lambda \end{array}\right){m}_{\pm }\left(x;z\right),{\mu }_{\pm ,2}\left(x;\lambda \right)=\left(\begin{array}{cc}{\lambda }^{-1} & 0\\ -u(x) & 1\end{array}\right){n}_{\pm }\left(x;z\right),\end{eqnarray}$
$\begin{eqnarray}{\mu }_{\pm ,1}\left(x;\lambda \right)=\left(\begin{array}{cc}1 & 0\\ -{\lambda }^{-1}v(x) & {\lambda }^{-1}\end{array}\right){\hat{m}}_{\pm }\left(x;z\right),{\mu }_{\pm ,2}\left(x;\lambda \right)=\left(\begin{array}{cc}\lambda & 0\\ -v(x) & 1\end{array}\right){\hat{n}}_{\pm }\left(x;z\right),\end{eqnarray}$
with the limit 10a ) yield uniqueness and analytic continuations of ${\mu }_{\pm ,1}\left(x;\lambda \right)$ and ${\mu }_{\mp ,2}\left(x;\lambda \right)$ in D± ∩ B0 with ${B}_{0}:= \left\{\lambda \in {\mathbb{C}}:\left|\lambda \right|\lt 1\right\}$, respectively. Analogously, by lemma 3 in [23], the right-hand sides of equation (10b ) yield uniqueness and analytic continuations of ${\mu }_{\pm ,1}\left(x;\lambda \right)$ and ${\mu }_{\mp ,2}\left(x;\lambda \right)$ in D± ∩ B∞ with ${B}_{\infty }:= \left\{\lambda \in {\mathbb{C}}:\left|\lambda \right|\gt 1\right\}$, respectively. Then we conclude the results below.
$\begin{eqnarray}\mathop{\,\rm{lim}\,}\limits_{\lambda \to 0}{m}_{\pm }\left(x;z\right)=\left(\begin{array}{c}{{\rm{e}}}^{-\frac{{\rm{i}}}{4}{\displaystyle \int }_{\pm \infty }^{x}\left(| u(y,t){| }^{2}+| v(y,t){| }^{2}\right){\rm{d}}y}\\ 0\end{array}\right),\mathop{\,\rm{lim}\,}\limits_{\lambda \to 0}{n}_{\pm }\left(x;z\right)=\left(\begin{array}{c}0\\ {{\rm{e}}}^{\frac{{\rm{i}}}{4}{\displaystyle \int }_{\pm \infty }^{x}\left(| u(y,t){| }^{2}+| v(y,t){| }^{2}\right){\rm{d}}y}\end{array}\right),\end{eqnarray}$
$\begin{eqnarray}\mathop{\,\rm{lim}\,}\limits_{| \lambda | \to \infty }{\hat{m}}_{\pm }\left(x;z\right)=\left(\begin{array}{c}{{\rm{e}}}^{\frac{{\rm{i}}}{4}{\displaystyle \int }_{\pm \infty }^{x}\left(| u(y,t){| }^{2}+| v(y,t){| }^{2}\right){\rm{d}}y}\\ 0\end{array}\right),\mathop{\,\rm{lim}\,}\limits_{| \lambda | \to \infty }{\hat{n}}_{\pm }\left(x;z\right)=\left(\begin{array}{c}0\\ {{\rm{e}}}^{-\frac{{\rm{i}}}{4}{\displaystyle \int }_{\pm \infty }^{x}\left(| u(y,t){| }^{2}+| v(y,t){| }^{2}\right){\rm{d}}y}\end{array}\right),\end{eqnarray}$
where ${\mu }_{\pm ,j}\left(x;\lambda \right)$ is the j-th column of the matrix functions ${\mu }_{\pm }\left(x;\lambda \right)$ $\left(j=1,2\right)$. ${{\mathbb{C}}}^{\pm }$ of plane z corresponds to D± of plane λ, where the analytical regions D+ and D− of the modified Jost solutions as well as the boundary Σ are defined as: $\begin{eqnarray}{D}^{+}:= \left\{\lambda \in {\mathbb{C}}| {\rm{Re}}\left(\lambda \right){\rm{Im}}\left(\lambda \right)\gt 0\right\},\quad {D}^{-}:= \left\{\lambda \in {\mathbb{C}}| {\rm{Re}}\left(\lambda \right){\rm{Im}}(\lambda )\lt 0\right\},\quad {\rm{\Sigma }}={\mathbb{R}}\cup {\rm{i}}{\mathbb{R}}\setminus \left\{0\right\},\end{eqnarray}$
which can be seen in figure 1. By lemma 1 in [23], the right-hand sides of equation (
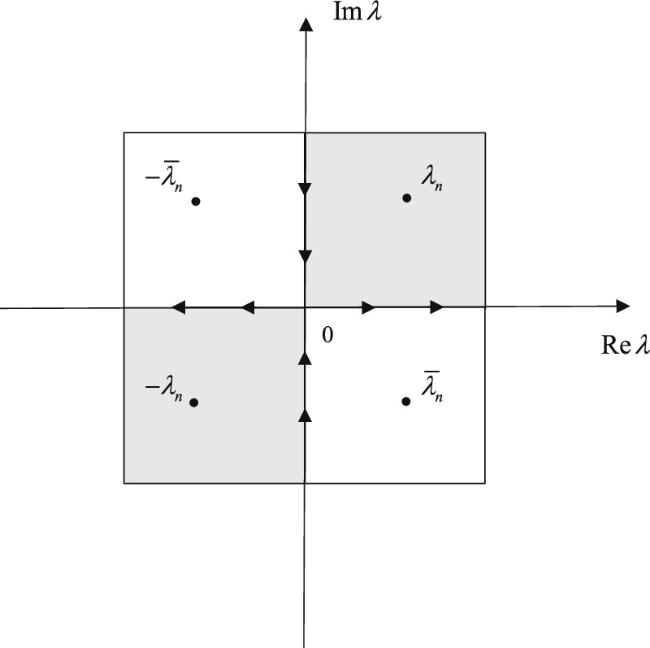
Figure 1. Complex λ-plane. The analytical regions D+ (grey) and D− (white) of the modified Jost solutions, discrete spectrum of the scattering problem and orientation of the contours for the RH problem. |
Suppose that $u\left(x,t\right),v\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)\cap {L}^{\infty }\left({\mathbb{R}}\right)$ and ${u}_{x}\left(x,t\right),{v}_{x}\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)$, the modified Jost solutions ${\mu }_{\pm }\left(x,t;\lambda \right)$ have the following properties:
(i) ${\mu }_{\pm }\left(x,t;\lambda \right)$ are unique for the modified Lax pair (9) satisfying ${\mu }_{\pm }\left(x,t;\lambda \right)\unicode{x0007E}I$ as x → ± ∞;
(ii) ${\mu }_{-,2}\left(x,t;\lambda \right)$, ${\mu }_{+,1}\left(x,t;\lambda \right)$ can be analytically extended to D+ and continuously extended to D+ ∪ Σ;
(iii) ${\mu }_{-,1}\left(x,t;\lambda \right)$, ${\mu }_{+,2}\left(x,t;\lambda \right)$ can be analytically extended to D− and continuously extended to D− ∪ Σ.
In view of equation (8 ), the Jost solutions ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$ naturally inherit the uniqueness, analyticity and continuity of ${\mu }_{\pm }\left(x,t;\lambda \right)$.
2.1.2. Scattering matrix and reflection coefficients
Since ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$ are both the solutions of Lax pair (3), thus they are linearly correlated by the relation
$\begin{eqnarray}{{\rm{\Phi }}}_{+}\left(x,t;\lambda \right)={{\rm{\Phi }}}_{-}\left(x,t;\lambda \right)S\left(\lambda \right),\quad \lambda \in {\rm{\Sigma }},\end{eqnarray}$
which can be written in the column-wise manner: $\begin{eqnarray}{{\rm{\Phi }}}_{+,1}\left(x,t;\lambda \right)={{\rm{\Phi }}}_{-,1}\left(x,t;\lambda \right){s}_{11}\left(\lambda \right)+{{\rm{\Phi }}}_{-,2}\left(x,t;\lambda \right){s}_{21}\left(\lambda \right),\end{eqnarray}$
$\begin{eqnarray}{{\rm{\Phi }}}_{+,2}\left(x,t;\lambda \right)={{\rm{\Phi }}}_{-,1}\left(x,t;\lambda \right){s}_{12}\left(\lambda \right)+{{\rm{\Phi }}}_{-,2}\left(x,t;\lambda \right){s}_{22}\left(\lambda \right),\end{eqnarray}$
where $S\left(\lambda \right)={\left({s}_{ij}\left(\lambda \right)\right)}_{2\times 2}$ is the scattering matrix that is independent of x and t, and the elements ${s}_{ij}\left(\lambda \right)$ $\left(i,j=1,2\right)$ are the scattering coefficients. In the usual way, the reflection coefficients are defined as $\begin{eqnarray}\rho \left(\lambda \right)=\frac{{s}_{21}\left(\lambda \right)}{{s}_{11}\left(\lambda \right)},\quad \hat{\rho }\left(\lambda \right)=\frac{{s}_{12}\left(\lambda \right)}{{s}_{22}\left(\lambda \right)},\quad \lambda \in {\rm{\Sigma }}.\end{eqnarray}$
By virtue of equation (13 ), ${\rm{\det }}{{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)=1$ implies that ${\rm{\det }}S\left(\lambda \right)=1$ and ${s}_{ij}\left(\lambda \right)$ has the following representations: 8 ) and (13 ), the relationship between ${\mu }_{+}\left(x,t;\lambda \right)$ and ${\mu }_{-}\left(x,t;\lambda \right)$ is given as
$\begin{eqnarray}\begin{array}{rcl}{s}_{11}\left(\lambda \right) & = & {\rm{\det }}\left({{\rm{\Phi }}}_{+,1}\left(x,t;\lambda \right),{{\rm{\Phi }}}_{-,2}\left(x,t;\lambda \right)\right),\quad {s}_{12}\left(\lambda \right)={\rm{\det }}\left({{\rm{\Phi }}}_{+,2}\left(x,t;\lambda \right),{{\rm{\Phi }}}_{-,2}\left(x,t;\lambda \right)\right),\\ {s}_{21}\left(\lambda \right) & = & {\rm{\det }}\left({{\rm{\Phi }}}_{-,1}\left(x,t;\lambda \right),{{\rm{\Phi }}}_{+,1}\left(x,t;\lambda \right)\right),\quad {s}_{22}\left(\lambda \right)={\rm{\det }}\left({{\rm{\Phi }}}_{-,1}\left(x,t;\lambda \right),{{\rm{\Phi }}}_{+,2}\left(x,t;\lambda \right)\right).\end{array}\end{eqnarray}$
According to equations ( $\begin{eqnarray}{\mu }_{+}\left(x,t;\lambda \right)={\mu }_{-}\left(x,t;\lambda \right){{\rm{e}}}^{{\rm{i}}\theta \left(x,t;\lambda \right){\sigma }_{3}}S\left(\lambda \right){{\rm{e}}}^{-{\rm{i}}\theta \left(x,t;\lambda \right){\sigma }_{3}},\quad \lambda \in {\rm{\Sigma }}.\end{eqnarray}$
Based on equation (16 ), the analyticity of scattering coefficients are obtained as follows:
Suppose that $u\left(x,t\right),v\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)\cap {L}^{\infty }\left({\mathbb{R}}\right)$ and ${u}_{x}\left(x,t\right),{v}_{x}\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)$, ${s}_{11}\left(\lambda \right)$ can be analytically extended to D+ and continuously extended to D+ ∪ Σ, ${s}_{22}\left(\lambda \right)$ can be analytically extended to D−and continuously extended to D− ∪ Σ, while both ${s}_{12}\left(\lambda \right)$ and ${s}_{21}\left(\lambda \right)$ are only continuous in Σ.
2.1.3. Symmetries
Considering the mappings $\lambda \mapsto \overline{\lambda }$ and $\lambda \mapsto -\overline{\lambda }$, we can obtain the following symmetry properties:
There exist two kinds of symmetries for $L\left(x,t;\lambda \right)$, $A\left(x,t;\lambda \right)$, ${\mu }_{\pm }\left(x,t;\lambda \right)$, ${{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)$, $S\left(\lambda \right)$ and $\rho \left(\lambda \right)$:
(i) The first symmetry $\left(\lambda \mapsto \overline{\lambda }\right)$
$\begin{eqnarray}L\left(x,t;\lambda \right)={\sigma }_{2}\overline{L\left(x,t;\overline{\lambda }\right)}{\sigma }_{2},\quad A\left(x,t;\lambda \right)={\sigma }_{2}\overline{A\left(x,t;\overline{\lambda }\right)}{\sigma }_{2},\end{eqnarray}$
$\begin{eqnarray}{\mu }_{\pm }\left(x,t;\lambda \right)={\sigma }_{2}\overline{{\mu }_{\pm }\left(x,t;\overline{\lambda }\right)}{\sigma }_{2},\quad {{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)={\sigma }_{2}\overline{{{\rm{\Phi }}}_{\pm }\left(x,t;\overline{\lambda }\right)}{\sigma }_{2},\end{eqnarray}$
$\begin{eqnarray}S\left(\lambda \right)={\sigma }_{2}\overline{S\left(\overline{\lambda }\right)}{\sigma }_{2},\quad \rho \left(\lambda \right)=-\overline{\hat{\rho }\left(\overline{\lambda }\right)},\quad {\sigma }_{2}=\left(\begin{array}{cc}0 & -{\rm{i}}\\ {\rm{i}} & 0\end{array}\right).\end{eqnarray}$
(ii) The second symmetry $\left(\lambda \mapsto -\overline{\lambda }\right)$
$\begin{eqnarray}L\left(x,t;\lambda \right)={\sigma }_{1}\overline{L\left(x,t;-\overline{\lambda }\right)}{\sigma }_{1},\quad A\left(x,t;\lambda \right)={\sigma }_{1}\overline{A\left(x,t;-\overline{\lambda }\right)}{\sigma }_{1},\end{eqnarray}$
$\begin{eqnarray}{\mu }_{\pm }\left(x,t;\lambda \right)={\sigma }_{1}\overline{{\mu }_{\pm }\left(x,t;-\overline{\lambda }\right)}{\sigma }_{1},\quad {{\rm{\Phi }}}_{\pm }\left(x,t;\lambda \right)={\sigma }_{1}\overline{{{\rm{\Phi }}}_{\pm }\left(x,t;-\overline{\lambda }\right)}{\sigma }_{1},\end{eqnarray}$
$\begin{eqnarray}S\left(\lambda \right)={\sigma }_{1}\overline{S\left(-\overline{\lambda }\right)}{\sigma }_{1},\quad \rho \left(\lambda \right)=\overline{\hat{\rho }\left(-\overline{\lambda }\right)},\quad {\sigma }_{1}=\left(\begin{array}{cc}0 & 1\\ 1 & 0\end{array}\right).\end{eqnarray}$
2.1.4. Asymptotic behaviors as λ → ∞
In order to formulate the RH problem, it is necessary to analyze the asymptotic behaviors of the modified Jost solutions ${\mu }_{\pm }\left(x,t;\lambda \right)$ and scattering matrix $S\left(\lambda \right)$ as λ → ∞. We consider the following expansions 9a ). Collecting the coefficients of λn$\left(n=0,1,2\right)$ yields the following results:
$\begin{eqnarray}{\mu }_{\pm }\left(x,t;\lambda \right)={\mu }_{\pm }^{(0)}\left(x,t\right)+\frac{{\mu }_{\pm }^{(1)}\left(x,t\right)}{\lambda }+\frac{{\mu }_{\pm }^{(2)}\left(x,t\right)}{{\lambda }^{2}}+{ \mathcal O }\left({\lambda }^{-3}\right),\quad \lambda \to \infty ,\end{eqnarray}$
and substitute them into equation ( $\begin{eqnarray}{\lambda }^{2}:\quad {\mu }_{\pm ,12}^{(0)}\left(x,t\right)={\mu }_{\pm ,21}^{(0)}\left(x,t\right)=0,\end{eqnarray}$
$\begin{eqnarray}{\lambda }^{1}:\quad {\mu }_{\pm ,12}^{(1)}\left(x,t\right)=\overline{v}\left(x,t\right)\,{\mu }_{\pm ,22}^{(0)}\left(x,t\right),\quad {\mu }_{\pm ,21}^{(1)}\left(x,t\right)=-v\left(x,t\right)\,{\mu }_{\pm ,11}^{(0)}\left(x,t\right),\end{eqnarray}$
$\begin{eqnarray}{\lambda }^{0}:\quad {\mu }_{\pm ,11}^{(0)}\left(x,t\right)={{\rm{e}}}^{{\rm{i}}{Q}_{\pm }\left(x,t\right)},\quad {\mu }_{\pm ,22}^{(0)}\left(x,t\right)={{\rm{e}}}^{-{\rm{i}}{Q}_{\pm }\left(x,t\right)},\end{eqnarray}$
with $\begin{eqnarray}{Q}_{\pm }\left(x,t\right)=\frac{1}{4}{\int }_{\pm \infty }^{x}\left(| u(y,t){| }^{2}+| v(y,t){| }^{2}\right){\rm{d}}y,\end{eqnarray}$
where ${\mu }_{\pm ,ij}^{(m)}$ represents the (i, j)-element of the matrix ${\mu }_{\pm }^{(m)}$. Then, we reach the following asymptotic results:The asymptotic behaviors of the modified Jost solutions and $S\left(\lambda \right)$ are given, respectively, as
$\begin{eqnarray}{\mu }_{\pm }\left(x,t;\lambda \right)={{\rm{e}}}^{{\rm{i}}{Q}_{\pm }\left(x,t\right){\sigma }_{3}}+{ \mathcal O }\left({\lambda }^{-1}\right),\quad S\left(\lambda \right)={{\rm{e}}}^{-{\rm{i}}{Q}_{0}{\sigma }_{3}}+{ \mathcal O }\left({\lambda }^{-1}\right),\quad \lambda \to \infty ,\end{eqnarray}$
with $\begin{eqnarray}{Q}_{0}=\frac{1}{4}{\int }_{-\infty }^{+\infty }\left(| u(y,t){| }^{2}+| v(y,t){| }^{2}\right){\rm{d}}y.\end{eqnarray}$
This proposition is consistent with equations (2.22) and (3.15) in [23].
2.2. Direct scattering for ω
In this section, we study the direct scattering for the case of λ → 0, i.e., ω → ∞. Similar but not repetitive to the process in section 2.1 , we perform the analysis on the new Lax pair about the parameter ω.
2.2.1. Lax pair, integral equations and analyticity of modified Jost solutions
As x → ± ∞, the asymptotic scattering problem about ω reads
$\begin{eqnarray}{\widetilde{{\rm{\Phi }}}}_{x}\left(x,t;\omega \right)={\widetilde{L}}_{\pm }\left(x,t;\omega \right)\widetilde{{\rm{\Phi }}}\left(x,t;\omega \right),\quad {\widetilde{L}}_{\pm }\left(x,t;\omega \right):= \frac{{\rm{i}}}{4}\left(\frac{1}{{\omega }^{2}}-{\omega }^{2}\right){\sigma }_{3},\end{eqnarray}$
$\begin{eqnarray}{\widetilde{{\rm{\Phi }}}}_{t}\left(x,t;\omega \right)={\widetilde{A}}_{\pm }\left(x,t;\omega \right)\widetilde{{\rm{\Phi }}}\left(x,t;\omega \right),\quad {\widetilde{A}}_{\pm }\left(x,t;\omega \right):= \frac{{\rm{i}}}{4}\left(\frac{1}{{\omega }^{2}}+{\omega }^{2}\right){\sigma }_{3}.\end{eqnarray}$
Note that the fundamental matrix solution ${\widetilde{{\rm{\Phi }}}}_{bg}\left(x,t;\omega \right)$ of equations (25) is given by 2.1 .
$\begin{eqnarray}{\widetilde{{\rm{\Phi }}}}_{bg}\left(x,t;\omega \right)={{\rm{e}}}^{{\rm{i}}\widetilde{\theta }\left(x,t;\omega \right){\sigma }_{3}},\quad \widetilde{\theta }\left(x,t;\omega \right)=\frac{1}{4}\left[\left(\frac{1}{{\omega }^{2}}-{\omega }^{2}\right)x+\left(\frac{1}{{\omega }^{2}}+{\omega }^{2}\right)t\right].\end{eqnarray}$
For the Jost solutions ${\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\omega \right)$ with the following asymptotic conditions $\begin{eqnarray}{\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\omega \right)\unicode{x0007E}{{\rm{e}}}^{{\rm{i}}\widetilde{\theta }\left(x,t;\omega \right){\sigma }_{3}},\quad x\to \pm \infty .\end{eqnarray}$
We can obtain that ${\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\omega \right)$ also satisfy equation (3), analogous to Proposition We introduce the modified Jost solutions ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)$ in the form 28 ) into equations (3) gives the modified Lax pair about ω:
$\begin{eqnarray}{\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)={\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\omega \right){{\rm{e}}}^{-{\rm{i}}\widetilde{\theta }\left(x,t;\omega \right){\sigma }_{3}},\end{eqnarray}$
where ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)\unicode{x0007E}I$ as x → ± ∞. Inserting equation ( $\begin{eqnarray}{\widetilde{\mu }}_{\pm ,x}\left(x,t;\omega \right)+\frac{{\rm{i}}}{4}\left(\frac{1}{{\omega }^{2}}-{\omega }^{2}\right)\left[{\widetilde{\mu }}_{\pm }\left(x,t;\omega \right),{\sigma }_{3}\right]={\widetilde{L}}_{1}\left(x,t;\omega \right){\widetilde{\mu }}_{\pm }\left(x,t;\omega \right),\end{eqnarray}$
$\begin{eqnarray}{\widetilde{\mu }}_{\pm ,t}\left(x,t;\omega \right)+\frac{{\rm{i}}}{4}\left(\frac{1}{{\omega }^{2}}+{\omega }^{2}\right)\left[{\widetilde{\mu }}_{\pm }\left(x,t;\omega \right),{\sigma }_{3}\right]={\widetilde{A}}_{1}\left(x,t;\omega \right){\widetilde{\mu }}_{\pm }\left(x,t;\omega \right).\end{eqnarray}$
Similarly, the analyticity of modified Jost solutions ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)$ can be derived.
Suppose that $u\left(x,t\right),v\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)\cap {L}^{\infty }\left({\mathbb{R}}\right)$, ${u}_{x}\left(x,t\right),{v}_{x}\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)$ and ${\widetilde{\mu }}_{\pm ,j}\left(x,t;\omega \right)$ is the j-th column of the matrix functions ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)$ $\left(j=1,2\right)$. Then, the modified Jost solutions ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)$ have the following properties:
(i) ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)$ are unique for the modified Lax pair (29) satisfying ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)\unicode{x0007E}I$ as x → ± ∞;
(ii) ${\widetilde{\mu }}_{-,2}\left(x,t;\omega \right)$, ${\widetilde{\mu }}_{+,1}\left(x,t;\omega \right)$ can be analytically extended to D− and continuously extended to D− ∪ Σ;
(iii) ${\widetilde{\mu }}_{-,1}\left(x,t;\omega \right)$, ${\widetilde{\mu }}_{+,2}\left(x,t;\omega \right)$ can be analytically extended to D+ and continuously extended to D+ ∪ Σ.
2.2.2. Scattering matrix and reflection coefficients
Since ${\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\omega \right)$ are both the solutions of Lax pair (3), thus they are linearly correlated by the relation 30 ) that ${\rm{\det }}\widetilde{S}\left(\omega \right)=1$ and ${\widetilde{s}}_{ij}\left(\omega \right)$ has the following representations: 28 ), there is the relationship between ${\widetilde{\mu }}_{+}\left(x,t;\omega \right)$ and ${\widetilde{\mu }}_{-}\left(x,t;\omega \right)$: 2.4 , we can obtain the analyticity of scattering coefficients about ω as follows:
$\begin{eqnarray}{\widetilde{{\rm{\Phi }}}}_{+}\left(x,t;\omega \right)={\widetilde{{\rm{\Phi }}}}_{-}\left(x,t;\omega \right)\widetilde{S}\left(\omega \right),\quad \omega \in {\rm{\Sigma }},\end{eqnarray}$
which, for the individual columns, is written as $\begin{eqnarray}{\widetilde{{\rm{\Phi }}}}_{+,1}\left(x,t;\omega \right)={\widetilde{{\rm{\Phi }}}}_{-,1}\left(x,t;\omega \right){\widetilde{s}}_{11}\left(\omega \right)+{\widetilde{{\rm{\Phi }}}}_{-,2}\left(x,t;\omega \right){\widetilde{s}}_{21}\left(\omega \right),\end{eqnarray}$
$\begin{eqnarray}{\widetilde{{\rm{\Phi }}}}_{+,2}\left(x,t;\omega \right)={\widetilde{{\rm{\Phi }}}}_{-,1}\left(x,t;\omega \right){\widetilde{s}}_{12}\left(\omega \right)+{\widetilde{{\rm{\Phi }}}}_{-,2}\left(x,t;\omega \right){\widetilde{s}}_{22}\left(\omega \right),\end{eqnarray}$
where $\widetilde{S}\left(\omega \right)={\left({\widetilde{s}}_{ij}\left(\omega \right)\right)}_{2\times 2}$ is the scattering matrix that is independent of x and t, and the elements ${\widetilde{s}}_{ij}\left(\omega \right)\left(i,j=1,2\right)$ are the scattering coefficients. Similarly, the reflection coefficients are defined as $\begin{eqnarray}\widetilde{\rho }\left(\omega \right)=\frac{{\widetilde{s}}_{21}\left(\omega \right)}{{\widetilde{s}}_{11}\left(\omega \right)},\quad \hat{\widetilde{\rho }}\left(\omega \right)=\frac{{\widetilde{s}}_{12}\left(\omega \right)}{{\widetilde{s}}_{22}\left(\omega \right)},\quad \omega \in {\rm{\Sigma }}.\end{eqnarray}$
It follows from equation ( $\begin{eqnarray}\begin{array}{rcl}{\widetilde{s}}_{11}\left(\omega \right) & = & {\rm{\det }}\left({\widetilde{{\rm{\Phi }}}}_{+,1}\left(x,t;\omega \right),{\widetilde{{\rm{\Phi }}}}_{-,2}\left(x,t;\omega \right)\right),\quad {\widetilde{s}}_{12}\left(\omega \right)={\rm{\det }}\left({\widetilde{{\rm{\Phi }}}}_{+,2}\left(x,t;\omega \right),{\widetilde{{\rm{\Phi }}}}_{-,2}\left(x,t;\omega \right)\right),\\ {\widetilde{s}}_{21}\left(\omega \right) & = & {\rm{\det }}\left({\widetilde{{\rm{\Phi }}}}_{-,1}\left(x,t;\omega \right),{\widetilde{{\rm{\Phi }}}}_{+,1}\left(x,t;\omega \right)\right),\quad {\widetilde{s}}_{22}\left(\omega \right)={\rm{\det }}\left({\widetilde{{\rm{\Phi }}}}_{-,1}\left(x,t;\omega \right),{\widetilde{{\rm{\Phi }}}}_{+,2}\left(x,t;\omega \right)\right).\end{array}\end{eqnarray}$
As implied by equation ( $\begin{eqnarray}{\widetilde{\mu }}_{+}\left(x,t;\omega \right)={\widetilde{\mu }}_{-}\left(x,t;\omega \right){{\rm{e}}}^{{\rm{i}}\widetilde{\theta }\left(x,t;\omega \right){\sigma }_{3}}\widetilde{S}\left(\omega \right){{\rm{e}}}^{-{\rm{i}}\widetilde{\theta }\left(x,t;\omega \right){\sigma }_{3}},\quad \omega \in {\rm{\Sigma }}.\end{eqnarray}$
Similar to Proposition Suppose that $u\left(x,t\right),v\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)\cap {L}^{\infty }\left({\mathbb{R}}\right)$ and ${u}_{x}\left(x,t\right),{v}_{x}\left(x,t\right)\in {L}^{1}\left({\mathbb{R}}\right)$, ${\widetilde{s}}_{11}\left(\omega \right)$ can be analytically extended to D−and continuously extended to D− ∪ Σ, ${\widetilde{s}}_{22}\left(\omega \right)$ can be analytically extended to D+ and continuously extended to D+ ∪ Σ, while both ${\widetilde{s}}_{12}\left(\omega \right)$ and ${\widetilde{s}}_{21}\left(\omega \right)$ are only continuous in Σ.
2.2.3. Symmetries
Considering the mapping $\omega \mapsto \overline{\omega }$ and $\omega \mapsto -\overline{\omega }$, we can derive the following symmetry properties:
There exist two kinds of symmetries for $\widetilde{L}(x,t;\omega )$, $\widetilde{A}(x,t;\omega )$, ${\widetilde{\mu }}_{\pm }(x,t;\omega )$, ${\widetilde{{\rm{\Phi }}}}_{\pm }(x,t;\omega )$, $\widetilde{S}(\omega )$ and $\widetilde{\rho }(\omega )$:
(i) The first symmetry $\left(\omega \mapsto \overline{\omega }\right)$
$\begin{eqnarray}\widetilde{L}\left(x,t;\omega \right)={\sigma }_{2}\overline{\widetilde{L}\left(x,t;\overline{\omega }\right)}{\sigma }_{2},\quad \widetilde{A}\left(x,t;\omega \right)={\sigma }_{2}\overline{\widetilde{A}\left(x,t;\overline{\omega }\right)}{\sigma }_{2},\end{eqnarray}$
$\begin{eqnarray}{\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)={\sigma }_{2}\overline{{\widetilde{\mu }}_{\pm }\left(x,t;\overline{\omega }\right)}{\sigma }_{2},\quad {\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\omega \right)={\sigma }_{2}\overline{{\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\overline{\omega }\right)}{\sigma }_{2},\end{eqnarray}$
$\begin{eqnarray}\widetilde{S}\left(\omega \right)={\sigma }_{2}\overline{\widetilde{S}\left(\overline{\omega }\right)}{\sigma }_{2},\quad \widetilde{\rho }\left(\omega \right)=-\overline{\hat{\widetilde{\rho }}\left(\overline{\omega }\right)}.\end{eqnarray}$
(ii) The second symmetry $\left(\omega \mapsto -\overline{\omega }\right)$
$\begin{eqnarray}\widetilde{L}\left(x,t;\omega \right)={\sigma }_{1}\overline{\widetilde{L}\left(x,t;-\overline{\omega }\right)}{\sigma }_{1},\quad \widetilde{A}\left(x,t;\omega \right)={\sigma }_{1}\overline{\widetilde{A}\left(x,t;-\overline{\omega }\right)}{\sigma }_{1},\end{eqnarray}$
$\begin{eqnarray}{\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)={\sigma }_{1}\overline{{\widetilde{\mu }}_{\pm }\left(x,t;-\overline{\omega }\right)}{\sigma }_{1},\quad {\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;\omega \right)={\sigma }_{1}\overline{{\widetilde{{\rm{\Phi }}}}_{\pm }\left(x,t;-\overline{\omega }\right)}{\sigma }_{1},\end{eqnarray}$
$\begin{eqnarray}\widetilde{S}\left(\omega \right)={\sigma }_{1}\overline{\widetilde{S}\left(-\overline{\omega }\right)}{\sigma }_{1},\quad \widetilde{\rho }\left(\omega \right)=\overline{\hat{\widetilde{\rho }}\left(-\overline{\omega }\right)}.\end{eqnarray}$
2.2.4. Asymptotic behaviors as ω → ∞
In order to construct the RH problem, it is also necessary to analyze the asymptotic behaviors of the modified Jost solutions ${\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)$ and scattering matrix $\widetilde{S}\left(\omega \right)$ as ω → ∞. We expand the modified Jost solutions about ω: 29a ). By collecting the coefficients of ωn$\left(n=0,1,2\right)$, we get the following results:
$\begin{eqnarray}{\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)={\widetilde{\mu }}_{\pm }^{(0)}\left(x,t\right)+\frac{{\widetilde{\mu }}_{\pm }^{(1)}\left(x,t\right)}{\omega }+\frac{{\widetilde{\mu }}_{\pm }^{(2)}\left(x,t\right)}{{\omega }^{2}}+{ \mathcal O }\left({\omega }^{-3}\right),\quad \omega \to \infty ,\end{eqnarray}$
and substitute them into equation ( $\begin{eqnarray}{\omega }^{2}:\quad {\widetilde{\mu }}_{\pm ,12}^{(0)}\left(x,t\right)={\widetilde{\mu }}_{\pm ,21}^{(0)}\left(x,t\right)=0,\end{eqnarray}$
$\begin{eqnarray}{\omega }^{1}:\quad {\widetilde{\mu }}_{\pm ,12}^{(1)}\left(x,t\right)=\overline{u}\left(x,t\right)\,{\widetilde{\mu }}_{\pm ,22}^{(0)}\left(x,t\right),\quad {\widetilde{\mu }}_{\pm ,21}^{(1)}\left(x,t\right)=-u\left(x,t\right)\,{\widetilde{\mu }}_{\pm ,11}^{(0)}\left(x,t\right),\end{eqnarray}$
$\begin{eqnarray}{\omega }^{0}:\quad {\widetilde{\mu }}_{\pm ,11}^{(0)}\left(x,t\right)={{\rm{e}}}^{-{\rm{i}}{Q}_{\pm }\left(x,t\right)},\quad {\widetilde{\mu }}_{\pm ,22}^{(0)}\left(x,t\right)={{\rm{e}}}^{{\rm{i}}{Q}_{\pm }\left(x,t\right)}.\end{eqnarray}$
Thus, the asymptotic behaviors of the modified Jost solutions and $\widetilde{S}\left(\omega \right)$ are obtained by
$\begin{eqnarray}{\widetilde{\mu }}_{\pm }\left(x,t;\omega \right)={{\rm{e}}}^{-{\rm{i}}{Q}_{\pm }\left(x,t\right){\sigma }_{3}}+{ \mathcal O }\left({\omega }^{-1}\right),\quad \widetilde{S}\left(\omega \right)={{\rm{e}}}^{{\rm{i}}{Q}_{0}{\sigma }_{3}}+{ \mathcal O }\left({\omega }^{-1}\right),\quad \omega \to \infty .\end{eqnarray}$
3. Inverse scattering
In this section, for the cases of spectral problems about λ and ω, we will study the inverse scattering including the RH problems, residue conditions, reconstruction formulas, trace formulas and soliton solutions under the reflectionless.
3.1. Inverse scattering for λ
3.1.1. Matrix RH problem
Recall that equation (13 ) establishes a relation between eigenfunctions analytic in D+ and those analytic in D−. Then, we define the sectionally meromorphic matrices: 2.6 , we obtain that
$\begin{eqnarray}{M}^{+}\left(x,t;\lambda \right)=\left(\frac{{\mu }_{+,1}\left(x,t;\lambda \right)}{{s}_{11}\left(\lambda \right)},{\mu }_{-,2}\left(x,t;\lambda \right)\right),\quad {M}^{-}\left(x,t;\lambda \right)=\left({\mu }_{-,1}\left(x,t;\lambda \right),\frac{{\mu }_{+,2}\left(x,t;\lambda \right)}{{s}_{22}\left(\lambda \right)}\right),\end{eqnarray}$
where the superscripts ± represent the analyticity in D+ and D−, respectively. Thus, the jump condition can be obtained as $\begin{eqnarray}{M}^{-}\left(x,t;\lambda \right)={M}^{+}\left(x,t;\lambda \right)\left(I-J\left(x,t;\lambda \right)\right),\quad \lambda \in {\rm{\Sigma }},\end{eqnarray}$
where $J\left(x,t;\lambda \right)$ is the jump matrix given by $\begin{eqnarray}J\left(x,t;\lambda \right)={{\rm{e}}}^{{\rm{i}}\theta \left(x,t;\lambda \right){\hat{\sigma }}_{3}}\left(\begin{array}{cc}0 & -\hat{\rho }\left(\lambda \right)\\ \rho \left(\lambda \right) & \rho \left(\lambda \right)\hat{\rho }\left(\lambda \right)\end{array}\right).\end{eqnarray}$
According to the asymptotic behaviors of the modified Jost solutions and scattering coefficients in Proposition $\begin{eqnarray}{M}^{\pm }\left(x,t;\lambda \right)={{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}+{ \mathcal O }\left({\lambda }^{-1}\right),\quad \lambda \to \infty .\end{eqnarray}$
In order to solve the RH problem, we remove the asymptotic behaviors and the pole contribution of $M\left(x,t;\lambda \right)$ and then obtain the normative RH problem
$\begin{eqnarray}\begin{array}{l}{M}^{-}\left(x,t;\lambda \right)-{{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\lambda ={\overline{\xi }}_{n}}{M}^{-}\left(x,t;\lambda \right)}{\lambda -{\overline{\xi }}_{n}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\lambda ={\xi }_{n}}{M}^{+}\left(x,t;\lambda \right)}{\lambda -{\xi }_{n}}\\ \quad ={M}^{+}\left(x,t;\lambda \right)-{{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\lambda ={\overline{\xi }}_{n}}{M}^{-}\left(x,t;\lambda \right)}{\lambda -{\overline{\xi }}_{n}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\lambda ={\xi }_{n}}{M}^{+}\left(x,t;\lambda \right)}{\lambda -{\xi }_{n}}-{M}^{+}\left(x,t;\lambda \right)J\left(x,t;\lambda \right).\end{array}\end{eqnarray}$
3.1.2. Residue conditions and reconstruction formula
Assume that λn$\left(1\leqslant n\leqslant N\right)$ are simple zeros of ${s}_{11}\left(\lambda \right)$ on region D+, that is, ${s}_{11}\left({\lambda }_{n}\right)=0$ but ${s}_{11}^{{\prime} }\left({\lambda }_{n}\right)\ne 0$. Immediately, the symmetries of the scattering matrix S(λ) show that
$\begin{eqnarray}{s}_{11}\left({\lambda }_{n}\right)={s}_{11}\left(-{\lambda }_{n}\right)={s}_{22}\left({\overline{\lambda }}_{n}\right)={s}_{22}\left(-{\overline{\lambda }}_{n}\right)=0.\end{eqnarray}$
For convenience, we set ξn = λn and ξN+n = − λn, 1≤n≤N. The discrete spectrum set is ${\left\{{\xi }_{n},{\overline{\xi }}_{n}\right\}}_{n=1}^{2N}$, where ξn ∈ D+ and ${\overline{\xi }}_{n}\in {D}^{-}$, as shown in figure 1.By, respectively, taking λ = ξn and $\lambda ={\overline{\xi }}_{n}$ in equation (17 ), the following relations are derived: 18b ) and (19b ) imply that 18b ).
$\begin{eqnarray}{\mu }_{+,1}\left(x,t;{\xi }_{n}\right)={b}_{n}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{n}\right)}{\mu }_{-,2}\left(x,t;{\xi }_{n}\right),\ {\mu }_{+,2}\left(x,t;{\overline{\xi }}_{n}\right)={\hat{b}}_{n}{{\rm{e}}}^{2{\rm{i}}\theta \left(x,t;{\overline{\xi }}_{n}\right)}{\mu }_{-,1}\left(x,t;{\overline{\xi }}_{n}\right),\ 1\leqslant n\leqslant 2N,\end{eqnarray}$
where bn and ${\hat{b}}_{n}$ are the norming constants in ${\mathbb{C}}$ that are independent on x and t. Meanwhile, the symmetries ( $\begin{eqnarray}{b}_{n}=-{b}_{N+n},\quad {b}_{m}=-{\overline{\hat{b}}}_{m},\quad 1\leqslant n\leqslant N,1\leqslant m\leqslant 2N.\end{eqnarray}$
Then, we obtain the residue conditions $\begin{eqnarray}\mathop{\,\rm{Res}\,}\limits_{\lambda ={\xi }_{n}}\left[\frac{{\mu }_{+,1}\left(x,t;\lambda \right)}{{s}_{11}\left(\lambda \right)}\right]={B}_{n}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{n}\right)}{\mu }_{-,2}\left(x,t;{\xi }_{n}\right),\quad {B}_{n}=\frac{{b}_{n}}{{s}_{11}^{{\prime} }\left({\xi }_{n}\right)},\quad 1\leqslant n\leqslant 2N,\end{eqnarray}$
$\begin{eqnarray}\mathop{\,\rm{Res}\,}\limits_{\lambda ={\overline{\xi }}_{n}}\left[\frac{{\mu }_{+,2}\left(x,t;\lambda \right)}{{s}_{22}\left(\lambda \right)}\right]={\hat{B}}_{n}{{\rm{e}}}^{2{\rm{i}}\theta \left(x,t;{\overline{\xi }}_{n}\right)}{\mu }_{-,1}\left(x,t;{\overline{\xi }}_{n}\right),\quad {\hat{B}}_{n}=\frac{{\hat{b}}_{n}}{{s}_{22}^{{\prime} }\left({\overline{\xi }}_{n}\right)},\quad 1\leqslant n\leqslant 2N,\end{eqnarray}$
where ${\overline{\hat{B}}}_{n}=-{B}_{n}$, as implied by the symmetries (Using the Plemelj's formula, we have the integral form for the solution of the RH problem 49 ) can be obtained as follows:
$\begin{eqnarray}\begin{array}{rcl}M\left(x,t;\lambda \right) & = & {{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}+\frac{1}{2\pi {\rm{i}}}{\displaystyle \int }_{{\rm{\Sigma }}}\frac{{M}^{+}\left(x,t;s\right)J\left(x,t;s\right)}{s-\lambda }{\rm{d}}s\\ & & +\displaystyle \sum _{n=1}^{2N}\left[\frac{{B}_{n}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{n}\right)}{\mu }_{-,2}\left(x,t;{\xi }_{n}\right)}{\lambda -{\xi }_{n}},\frac{-{\overline{B}}_{n}{{\rm{e}}}^{2{\rm{i}}\theta \left(x,t;{\overline{\xi }}_{n}\right)}{\mu }_{-,1}\left(x,t;{\overline{\xi }}_{n}\right)}{\lambda -{\overline{\xi }}_{n}}\right],\end{array}\end{eqnarray}$
where $\lambda \in {\mathbb{C}}$\Σ. By, respectively, taking λ = ξn and $\lambda ={\overline{\xi }}_{n}$, the second column of ${M}^{+}\left(x,t;\lambda \right)$ and the first column of ${M}^{-}\left(x,t;\lambda \right)$ in equation ( $\begin{eqnarray}{\mu }_{-,2}\left(x,t;{\xi }_{n}\right)=\left(\begin{array}{c}0\\ {{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right)}\end{array}\right)+\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{{\left[{M}^{+}\left(x,t;s\right)J\left(x,t;s\right)\right]}_{2}}{s-{\xi }_{n}}{\rm{d}}s-\displaystyle \sum _{k=1}^{2N}\frac{{\overline{B}}_{k}{{\rm{e}}}^{2{\rm{i}}\theta \left(x,t;{\overline{\xi }}_{k}\right)}{\mu }_{-,1}\left(x,t;{\overline{\xi }}_{k}\right)}{{\xi }_{n}-{\overline{\xi }}_{k}},\end{eqnarray}$
$\begin{eqnarray}{\mu }_{-,1}\left(x,t;{\overline{\xi }}_{n}\right)=\left(\begin{array}{c}{{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right)}\\ 0\end{array}\right)+\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{{\left[{M}^{+}\left(x,t;s\right)J\left(x,t;s\right)\right]}_{1}}{s-{\overline{\xi }}_{n}}{\rm{d}}s+\displaystyle \sum _{j=1}^{2N}\frac{{B}_{j}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{j}\right)}{\mu }_{-,2}\left(x,t;{\xi }_{j}\right)}{{\overline{\xi }}_{n}-{\xi }_{j}},\end{eqnarray}$
where ${\left[{M}^{+}\left(x,t;s\right)J\left(x,t;s\right)\right]}_{i}$ (i = 1, 2) is the i-th column of the matrix ${M}^{+}\left(x,t;s\right)J\left(x,t;s\right)$. Equations (50) will be used to derive the solution v of system (2) for the reflectionless case.When λ → ∞, equation (49 ) has the following form of asymptotic expansion 51 ) and ${\mu }_{-}\left(x,t;\lambda \right)$ in equation (20 ), we obtain the reconstruction formula for the component v with simple poles by matching ${ \mathcal O }\left({\lambda }^{-1}\right)$ term,
$\begin{eqnarray}M\left(x,t;\lambda \right)={{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}+\frac{{M}^{[1]}\left(x,t\right)}{\lambda }+{ \mathcal O }\left({\lambda }^{-2}\right),\end{eqnarray}$
where $\begin{eqnarray*}\begin{array}{rcl}{M}^{[1]}\left(x,t\right) & = & \displaystyle \sum _{n=1}^{2N}\left[{B}_{n}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{n}\right)}{\mu }_{-,2}\left(x,t;{\xi }_{n}\right),-{\overline{B}}_{n}{{\rm{e}}}^{2{\rm{i}}\theta \left(x,t;{\overline{\xi }}_{n}\right)}{\mu }_{-,1}\left(x,t;{\overline{\xi }}_{n}\right)\right]\\ & & -\frac{1}{2\pi {\rm{i}}}{\displaystyle \int }_{{\rm{\Sigma }}}{M}^{+}\left(x,t;s\right)J\left(x,t;s\right){\rm{d}}s.\end{array}\end{eqnarray*}$
Selecting the (2, 1)-element of ${M}^{-}\left(x,t;\lambda \right)$ in equation ( $\begin{eqnarray}v{{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right)}=-\displaystyle \sum _{n=1}^{2N}{B}_{n}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{n}\right)}{\mu }_{-,22}\left(x,t;{\xi }_{n}\right)+\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}{\left[{M}^{+}\left(x,t;s\right)J\left(x,t;s\right)\right]}_{21}{\rm{d}}s,\end{eqnarray}$
where ${\mu }_{\pm ,ij}\left(x,t;\lambda \right)$ represents the (i, j)-element of the matrix ${\mu }_{\pm }\left(x,t;\lambda \right)$, ${\left[{M}^{+}\left(x,t;s\right)J\left(x,t;s\right)\right]}_{ij}$ represents the (i, j)-element of the matrix ${M}^{+}\left(x,t;s\right)J\left(x,t;s\right)$.3.1.3. Trace formulas
Let us define that
$\begin{eqnarray}{\beta }^{+}\left(\lambda \right)={s}_{11}\left(\lambda \right)\displaystyle \prod _{n=1}^{2N}\frac{\lambda -{\overline{\xi }}_{n}}{\lambda -{\xi }_{n}},\quad {\beta }^{-}\left(\lambda \right)={s}_{22}\left(\lambda \right)\displaystyle \prod _{n=1}^{2N}\frac{\lambda -{\xi }_{n}}{\lambda -{\overline{\xi }}_{n}},\end{eqnarray}$
which satisfies the relation ${\beta }^{+}\left(\lambda \right){\beta }^{-}\left(\lambda \right)={s}_{11}\left(\lambda \right){s}_{22}\left(\lambda \right)$, λ ∈ Σ. According to the distribution of the zeros of the scattering coefficients, ${\beta }^{+}\left(\lambda \right)$ and ${\beta }^{-}\left(\lambda \right)$ are analytic on D+ and D−, respectively.Recalling ${\rm{\det }}S\left(\lambda \right)=1$, we have
$\begin{eqnarray}\frac{1}{{s}_{11}\left(\lambda \right){s}_{22}\left(\lambda \right)}=\frac{{s}_{11}\left(\lambda \right){s}_{22}\left(\lambda \right)-{s}_{12}\left(\lambda \right){s}_{21}\left(\lambda \right)}{{s}_{11}\left(\lambda \right){s}_{22}\left(\lambda \right)}=1-\rho \left(\lambda \right)\hat{\rho }\left(\lambda \right),\end{eqnarray}$
so that $\begin{eqnarray}{\beta }^{+}\left(\lambda \right){\beta }^{-}\left(\lambda \right)=\frac{1}{1-\rho \left(\lambda \right)\hat{\rho }\left(\lambda \right)},\quad \lambda \in {\rm{\Sigma }}.\end{eqnarray}$
Taking a logarithm to the above equation and using the Plemelj' formula, we have $\begin{eqnarray}{\rm{log}}{\beta }^{\pm }\left(\lambda \right)={\beta }_{1}\mp \frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\rho \left(s\right)\hat{\rho }\left(s\right)\right]}{s-\lambda }{\rm{d}}s,\quad \lambda \in {D}^{\pm },\end{eqnarray}$
where β1 is an arbitrary constant, that can be determined by the boundary values and asymptotic conditions.Hence, substituting equation (56 ) into equation (53 ) and using equation (23 ) lead to
$\begin{eqnarray}{s}_{11}\left(\lambda \right)={\rm{\exp }}\left[-{\rm{i}}{Q}_{0}-\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\rho \left(s\right)\hat{\rho }\left(s\right)\right]}{s-\lambda }{\rm{d}}s\right]\displaystyle \prod _{n=1}^{2N}\frac{\lambda -{\xi }_{n}}{\lambda -{\overline{\xi }}_{n}},\quad \lambda \in {D}^{+},\end{eqnarray}$
$\begin{eqnarray}{s}_{22}\left(\lambda \right)={\rm{\exp }}\left[{\rm{i}}{Q}_{0}+\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\rho \left(s\right)\hat{\rho }\left(s\right)\right]}{s-\lambda }{\rm{d}}s\right]\displaystyle \prod _{n=1}^{2N}\frac{\lambda -{\overline{\xi }}_{n}}{\lambda -{\xi }_{n}},\quad \lambda \in {D}^{-}.\end{eqnarray}$
Letting λ → 0, we get the following result from equation (57a ),
$\begin{eqnarray}{Q}_{0}=\frac{1}{4\pi }{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\rho \left(s\right)\hat{\rho }\left(s\right)\right]}{s}{\rm{d}}s+2\displaystyle \sum _{n=1}^{N}{\rm{\arg }}\left({\xi }_{n}\right).\end{eqnarray}$
3.1.4. Solution v for the reflectionless case
In the following, we derive solution v under the reflectionless condition (i.e., ρ(λ) = 0, $\hat{\rho }(\lambda )=0$). Looking at $\theta (x,t;\overline{\lambda })=\overline{\theta }(x,t;\lambda )$, it is convenient to introduce the functions ${f}_{j}\left(x,t;\lambda \right)=\frac{{B}_{j}}{\lambda -{\xi }_{j}}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{j}\right)}$(j = 1, …, 2N). The algebraic system can be obtained by extracting the second component of equations (50 ), that is,
$\begin{eqnarray}{\mu }_{-,22}\left(x,t;{\xi }_{n}\right)={{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right)}-\displaystyle \sum _{k=1}^{2N}{\overline{f}}_{k}\left(x,t;{\overline{\xi }}_{n}\right){\mu }_{-,21}\left(x,t;{\overline{\xi }}_{k}\right),\end{eqnarray}$
$\begin{eqnarray}{\mu }_{-,21}\left(x,t;{\overline{\xi }}_{n}\right)=\displaystyle \sum _{j=1}^{2N}{f}_{j}\left(x,t;{\overline{\xi }}_{n}\right){\mu }_{-,22}\left(x,t;{\xi }_{j}\right),\quad n=1,\ldots ,2N.\end{eqnarray}$
Substituting equation (59b ) into equation (59a ) yields 60 ) can be rewritten in the matrix form HX = G, where $H=I+F=\left({H}_{1},{H}_{2},\cdots \,,{H}_{2N}\right)$. Via Cramer's rule, solving this matrix equation yields ${X}_{n}=\frac{{\rm{\det }}\left({H}_{n}^{{\rm{r}}{\rm{e}}{\rm{p}}}\right)}{{\rm{\det }}\left(H\right)}$, where ${H}_{n}^{{\rm{r}}{\rm{e}}{\rm{p}}}=\left({H}_{1},{H}_{2}\cdots \,,{H}_{n-1},G,{H}_{n+1},\cdots \,,{H}_{2N}\right)$ and n = 1, …, 2N.
$\begin{eqnarray}{\mu }_{-,22}\left(x,t;{\xi }_{n}\right)={{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right)}-\displaystyle \sum _{k=1}^{2N}\displaystyle \sum _{j=1}^{2N}{\overline{f}}_{k}\left(x,t;{\overline{\xi }}_{n}\right){f}_{j}\left(x,t;{\overline{\xi }}_{k}\right){\mu }_{-,22}\left(x,t;{\xi }_{j}\right),\quad n=1,\ldots ,2N.\end{eqnarray}$
Introducing $\begin{eqnarray*}\begin{array}{rcl}{\boldsymbol{X}} & = & {\left({X}_{1},{X}_{2},\cdots \,,{X}_{2N}\right)}^{{\rm{T}}},\quad {X}_{n}={\mu }_{-,22}\left(x,t;{\xi }_{n}\right),\quad {\boldsymbol{G}}={\left({G}_{1},{G}_{2},\cdots \,,{G}_{2N}\right)}^{{\rm{T}}},\quad {G}_{n}={{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right)},\\ F & = & {\left({F}_{n,j}\right)}_{2N\times 2N},\quad {F}_{n,j}=\displaystyle \sum _{k=1}^{2N}{\overline{f}}_{k}\left(x,t;{\overline{\xi }}_{n}\right){f}_{j}\left(x,t;{\overline{\xi }}_{k}\right),\end{array}\end{eqnarray*}$
equation (Finally, substituting Xn's into the reconstruction formula (52 ), we get the solution v in the form of determinants
$\begin{eqnarray}v=\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}{{\rm{e}}}^{-2{\rm{i}}{Q}_{-}\left(x,t\right)},\end{eqnarray}$
where Haug is the (2N + 1) × (2N + 1) matrix $\begin{eqnarray*}{H}^{{\rm{a}}{\rm{u}}{\rm{g}}}=\left(\begin{array}{cc}0 & Y\\ {\boldsymbol{1}} & H\end{array}\right),\quad Y=\left({Y}_{1},{Y}_{2},\cdots \,,{Y}_{2N}\right),\quad {Y}_{n}={B}_{n}{{\rm{e}}}^{-2{\rm{i}}\theta \left(x,t;{\xi }_{n}\right)}.\end{eqnarray*}$
3.2. Inverse scattering for ω
In this section, we will discuss the inverse problem for the case of ω → ∞ similar to the process in section 3.1 .
3.2.1. Matrix RH problem
Similarly, the sectionally meromorphic matrices corresponding to ω are defined as follows: 39 ), we obtain that
$\begin{eqnarray}{\widetilde{M}}^{-}\left(x,t;\omega \right)=\left(\frac{{\widetilde{\mu }}_{+,1}\left(x,t;\omega \right)}{{\widetilde{s}}_{11}\left(\omega \right)},{\widetilde{\mu }}_{-,2}\left(x,t;\omega \right)\right),\quad {\widetilde{M}}^{+}\left(x,t;\omega \right)=\left({\widetilde{\mu }}_{-,1}\left(x,t;\omega \right),\frac{{\widetilde{\mu }}_{+,2}\left(x,t;\omega \right)}{{\widetilde{s}}_{22}\left(\omega \right)}\right).\end{eqnarray}$
Then, the jump condition is given by $\begin{eqnarray}{\widetilde{M}}^{+}\left(x,t;\omega \right)={\widetilde{M}}^{-}\left(x,t;\omega \right)\left(I-\widetilde{J}\left(x,t;\omega \right)\right),\quad \omega \in {\rm{\Sigma }},\end{eqnarray}$
where the jump matrix $\widetilde{J}\left(x,t;\omega \right)$ is $\begin{eqnarray}\widetilde{J}\left(x,t;\omega \right)={{\rm{e}}}^{{\rm{i}}\widetilde{\theta }\left(x,t;\omega \right){\hat{\sigma }}_{3}}\left(\begin{array}{cc}0 & -\hat{\widetilde{\rho }}\left(\omega \right)\\ \widetilde{\rho }\left(\omega \right) & \widetilde{\rho }\left(\omega \right)\hat{\widetilde{\rho }}\left(\omega \right)\end{array}\right).\end{eqnarray}$
According to the asymptotic behaviors of the Jost eigenfunctions and scattering coefficients in equation ( $\begin{eqnarray}{\widetilde{M}}^{\pm }\left(x,t;\omega \right)={{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}+{ \mathcal O }\left({\omega }^{-1}\right),\quad \omega \to \infty .\end{eqnarray}$
Again, by removing the asymptotic behaviors and pole contribution of $\widetilde{M}\left(x,t;\omega \right)$, we transform equation (63 ) into the normative RH problem:
$\begin{eqnarray}\begin{array}{l}{\widetilde{M}}^{+}\left(x,t;\omega \right)-{{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\omega ={\overline{\eta }}_{n}}{\widetilde{M}}^{+}\left(x,t;\omega \right)}{\omega -{\overline{\eta }}_{n}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\omega ={\eta }_{n}}{\widetilde{M}}^{-}\left(x,t;\omega \right)}{\omega -{\eta }_{n}}\\ \quad =\,{\widetilde{M}}^{-}\left(x,t;\omega \right)-{{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\omega ={\overline{\eta }}_{n}}{\widetilde{M}}^{+}\left(x,t;\omega \right)}{\omega -{\overline{\eta }}_{n}}-\displaystyle \sum _{n=1}^{2N}\frac{\mathop{\,\rm{Res}\,}\limits_{\omega ={\eta }_{n}}{\widetilde{M}}^{-}\left(x,t;\omega \right)}{\omega -{\eta }_{n}}-{\widetilde{M}}^{-}\left(x,t;\omega \right)\widetilde{J}\left(x,t;\omega \right).\end{array}\end{eqnarray}$
3.2.2. Residue conditions and reconstruction formula
Assume that ωn$\left(1\leqslant n\leqslant N\right)$ are simple zeros of ${\widetilde{s}}_{11}\left(\omega \right)$ on region D−, that is ${\widetilde{s}}_{11}\left({\omega }_{n}\right)=0$ but ${\widetilde{s}}_{11}^{{\prime} }\left({\omega }_{n}\right)\ne 0$. The symmetries of scattering matrix $\widetilde{S}\left(\omega \right)$ imply that
$\begin{eqnarray}{\widetilde{s}}_{11}\left({\omega }_{n}\right)={\widetilde{s}}_{11}\left(-{\omega }_{n}\right)={\widetilde{s}}_{22}\left({\overline{\omega }}_{n}\right)={\widetilde{s}}_{22}\left(-{\overline{\omega }}_{n}\right)=0.\end{eqnarray}$
For convenience, we set ηn = ωn and ηN+n = − ωn$\left(1\leqslant n\leqslant N\right)$. The discrete eigenvalues are ${\left\{{\eta }_{n},{\overline{\eta }}_{n}\right\}}_{n=1}^{2N}$, where ηn ∈ D− and ${\overline{\eta }}_{n}\in {D}^{+}$.By taking ω = ηn and $\omega ={\overline{\eta }}_{n}$ in equation (34 ), respectively, we get the relations: 35b ) and (36b ), we have 46 ) with equation (68 ) as x → ± ∞ further shows that 35b ).
$\begin{eqnarray}{\widetilde{\mu }}_{+,1}\left(x,t;{\eta }_{n}\right)={c}_{n}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{n}\right)}{\widetilde{\mu }}_{-,2}\left(x,t;{\eta }_{n}\right),\quad {\widetilde{\mu }}_{+,2}\left(x,t;{\overline{\eta }}_{n}\right)={\hat{c}}_{n}{{\rm{e}}}^{2{\rm{i}}\widetilde{\theta }\left(x,t;{\overline{\eta }}_{n}\right)}{\widetilde{\mu }}_{-,1}\left(x,t;{\overline{\eta }}_{n}\right),\quad 1\leqslant n\leqslant 2N,\end{eqnarray}$
where cn and ${\hat{c}}_{n}$ in ${\mathbb{C}}$ are the norming constants that are independent on x and t. Based on the symmetries ( $\begin{eqnarray}{c}_{n}=-{c}_{N+n},\quad {c}_{m}=-{\overline{\hat{c}}}_{m},\quad 1\leqslant n\leqslant N,\ 1\leqslant m\leqslant 2N.\end{eqnarray}$
Meanwhile, comparing equation ( $\begin{eqnarray}{b}_{n}={c}_{n},\quad 1\leqslant n\leqslant 2N.\end{eqnarray}$
Then, calculating the resides of ${\widetilde{M}}^{\pm }\left(x,t;\omega \right)$ at ω = ηn and $\omega ={\overline{\eta }}_{n}$ yields that $\begin{eqnarray}\mathop{\,\rm{Res}\,}\limits_{\omega ={\eta }_{n}}\left[\frac{{\widetilde{\mu }}_{+,1}\left(x,t;\omega \right)}{{\widetilde{s}}_{11}\left(\omega \right)}\right]={E}_{n}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{n}\right)}{\widetilde{\mu }}_{-,2}\left(x,t;{\eta }_{n}\right),\quad {E}_{n}=\frac{{c}_{n}}{{\widetilde{s}}_{11}^{{\prime} }\left({\eta }_{n}\right)},\quad 1\leqslant n\leqslant 2N,\end{eqnarray}$
$\begin{eqnarray}\mathop{\,\rm{Res}\,}\limits_{\omega ={\overline{\eta }}_{n}}\left[\frac{{\widetilde{\mu }}_{+,2}\left(x,t;\omega \right)}{{\widetilde{s}}_{22}\left(\omega \right)}\right]={\hat{E}}_{n}{{\rm{e}}}^{2{\rm{i}}\widetilde{\theta }\left(x,t;{\overline{\eta }}_{n}\right)}{\widetilde{\mu }}_{-,1}\left(x,t;{\overline{\eta }}_{n}\right),\quad {\hat{E}}_{n}=\frac{{\hat{c}}_{n}}{{\widetilde{s}}_{22}^{{\prime} }\left({\overline{\eta }}_{n}\right)},\quad 1\leqslant n\leqslant 2N,\end{eqnarray}$
where ${\overline{\hat{E}}}_{n}=-{E}_{n}$, as suggested by the symmetries (Using the Plemelj's formula, the solution of the RH problem (66 ) can be given in the following form 72 ) can be written as
$\begin{eqnarray}\begin{array}{rcl}\widetilde{M}\left(x,t;\omega \right) & = & {{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}-\frac{1}{2\pi {\rm{i}}}{\displaystyle \int }_{{\rm{\Sigma }}}\frac{{\widetilde{M}}^{-}\left(x,t;s\right)\widetilde{J}\left(x,t;s\right)}{s-\omega }{\rm{d}}s\\ & & +\displaystyle \sum _{n=1}^{2N}\left[\frac{{E}_{n}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{n}\right)}{\widetilde{\mu }}_{-,2}\left(x,t;{\eta }_{n}\right)}{\omega -{\eta }_{n}},\frac{-{\overline{E}}_{n}{{\rm{e}}}^{2{\rm{i}}\widetilde{\theta }\left(x,t;{\overline{\eta }}_{n}\right)}{\widetilde{\mu }}_{-,1}\left(x,t;{\overline{\eta }}_{n}\right)}{\omega -{\overline{\eta }}_{n}}\right],\end{array}\end{eqnarray}$
where $\omega \in {\mathbb{C}}$\Σ. By, respectively, taking ω = ηn and $\omega ={\overline{\eta }}_{n}$, the second column of ${\widetilde{M}}^{-}\left(x,t;\omega \right)$ and the first column of ${\widetilde{M}}^{+}\left(x,t;\omega \right)$ in equation ( $\begin{eqnarray}{\widetilde{\mu }}_{-,2}\left(x,t;{\eta }_{n}\right)=\left(\begin{array}{c}0\\ {{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right)}\end{array}\right)-\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{{\left[{\widetilde{M}}^{-}\left(x,t;s\right)\widetilde{J}\left(x,t;s\right)\right]}_{2}}{s-{\eta }_{n}}{\rm{d}}s-\displaystyle \sum _{k=1}^{2N}\frac{{\overline{E}}_{k}{{\rm{e}}}^{2{\rm{i}}\widetilde{\theta }\left(x,t;{\overline{\eta }}_{k}\right)}{\widetilde{\mu }}_{-,1}\left(x,t;{\overline{\eta }}_{k}\right)}{{\eta }_{n}-{\overline{\eta }}_{k}},\end{eqnarray}$
$\begin{eqnarray}{\widetilde{\mu }}_{-,1}\left(x,t;{\overline{\eta }}_{n}\right)=\left(\begin{array}{c}{{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right)}\\ 0\end{array}\right)-\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{{\left[{\widetilde{M}}^{-}\left(x,t;s\right)\widetilde{J}\left(x,t;s\right)\right]}_{1}}{s-{\overline{\eta }}_{n}}{\rm{d}}s+\displaystyle \sum _{j=1}^{2N}\frac{{E}_{j}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{j}\right)}{\widetilde{\mu }}_{-,2}\left(x,t;{\eta }_{j}\right)}{{\overline{\eta }}_{n}-{\eta }_{j}},\end{eqnarray}$
which will be used to construct the solution u of system (2) for the reflectionless case.When ω → ∞, the asymptotic expansion of equation (72 ) is given by 74 ) and ${\widetilde{\mu }}_{-}\left(x,t;\omega \right)$ in equation (37 ), we obtain the reconstruction formula for the component u with simple poles by matching ${ \mathcal O }\left({\omega }^{-1}\right)$ term, i.e.,
$\begin{eqnarray}\widetilde{M}\left(x,t;\omega \right)={{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right){\sigma }_{3}}+\frac{{\widetilde{M}}^{[1]}\left(x,t\right)}{\omega }+{ \mathcal O }\left({\omega }^{-2}\right),\end{eqnarray}$
where $\begin{eqnarray*}{\widetilde{M}}^{[1]}\left(x,t\right)=\displaystyle \sum _{n=1}^{2N}\left[{E}_{n}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{n}\right)}{\widetilde{\mu }}_{-,2}\left(x,t;{\eta }_{n}\right),-{\overline{E}}_{n}{{\rm{e}}}^{2{\rm{i}}\widetilde{\theta }\left(x,t;{\overline{\eta }}_{n}\right)}{\widetilde{\mu }}_{-,1}\left(x,t;{\overline{\eta }}_{n}\right)\right]+\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}{\widetilde{M}}^{-}\left(x,t;s\right)\widetilde{J}\left(x,t;s\right){\rm{d}}s.\end{eqnarray*}$
Selecting the $\left(2,1\right)$-element of ${\widetilde{M}}^{+}\left(x,t;\omega \right)$ in equation ( $\begin{eqnarray}u{{\rm{e}}}^{-{\rm{i}}{Q}_{-}\left(x,t\right)}=-\displaystyle \sum _{n=1}^{2N}{E}_{n}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{n}\right)}{\widetilde{\mu }}_{-,22}\left(x,t;{\eta }_{n}\right)-\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}{\left[{\widetilde{M}}^{-}\left(x,t;s\right)\widetilde{J}\left(x,t;s\right)\right]}_{21}{\rm{d}}s.\end{eqnarray}$
3.2.3. Trace formulas
Let us define that
$\begin{eqnarray}{\widetilde{\beta }}^{-}\left(\omega \right)={\widetilde{s}}_{11}\left(\omega \right)\displaystyle \prod _{n=1}^{2N}\frac{\omega -{\overline{\eta }}_{n}}{\omega -{\eta }_{n}},\quad {\widetilde{\beta }}^{+}\left(\omega \right)={\widetilde{s}}_{22}\left(\omega \right)\displaystyle \prod _{n=1}^{2N}\frac{\omega -{\eta }_{n}}{\omega -{\overline{\eta }}_{n}},\end{eqnarray}$
where ${\widetilde{\beta }}^{-}\left(\omega \right){\widetilde{\beta }}^{+}\left(\omega \right)={\widetilde{s}}_{11}\left(\omega \right){\widetilde{s}}_{22}\left(\omega \right)$, ω ∈ Σ. According to the distribution of the zeros of the scattering coefficients, ${\widetilde{\beta }}^{-}\left(\omega \right)$ and ${\widetilde{\beta }}^{+}\left(\omega \right)$ are analytical on D− and D+, respectively.Since ${\rm{\det }}\widetilde{S}\left(\omega \right)=1$, we have
$\begin{eqnarray}\frac{1}{{\widetilde{s}}_{11}\left(\omega \right){\widetilde{s}}_{22}\left(\omega \right)}=\frac{{\widetilde{s}}_{11}\left(\omega \right){\widetilde{s}}_{22}\left(\omega \right)-{\widetilde{s}}_{12}\left(\omega \right){\widetilde{s}}_{21}\left(\omega \right)}{{\widetilde{s}}_{11}\left(\omega \right){\widetilde{s}}_{22}\left(\omega \right)}=1-\widetilde{\rho }\left(\omega \right)\hat{\widetilde{\rho }}\left(\omega \right),\end{eqnarray}$
which says that $\begin{eqnarray}{\widetilde{\beta }}^{-}\left(\omega \right){\widetilde{\beta }}^{+}\left(\omega \right)=\frac{1}{1-\widetilde{\rho }\left(\omega \right)\hat{\widetilde{\rho }}\left(\omega \right)},\quad \omega \in {\rm{\Sigma }}.\end{eqnarray}$
Taking logarithm to the above equation and using the Plemelj' formula, we have $\begin{eqnarray}{\rm{log}}{\widetilde{\beta }}^{\pm }\left(\omega \right)={\beta }_{2}\mp \frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\widetilde{\rho }\left(s\right)\hat{\widetilde{\rho }}\left(s\right)\right]}{s-\omega }{\rm{d}}s,\quad \omega \in {D}^{\pm },\end{eqnarray}$
where β2 is an arbitrary constant, that can be determined by the boundary values and asymptotic conditions.Substituting equation (79 ) into equation (76 ) and using equation (39 ) gives
$\begin{eqnarray}{\widetilde{s}}_{11}\left(\omega \right)={\rm{\exp }}\left[{\rm{i}}{Q}_{0}-\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\widetilde{\rho }\left(s\right)\hat{\widetilde{\rho }}\left(s\right)\right]}{s-\omega }{\rm{d}}s\right]\displaystyle \prod _{n=1}^{2N}\frac{\omega -{\eta }_{n}}{\omega -{\overline{\eta }}_{n}},\quad \omega \in {D}^{-},\end{eqnarray}$
$\begin{eqnarray}{\widetilde{s}}_{22}\left(\omega \right)={\rm{\exp }}\left[-{\rm{i}}{Q}_{0}+\frac{1}{2\pi {\rm{i}}}{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\widetilde{\rho }\left(s\right)\hat{\widetilde{\rho }}\left(s\right)\right]}{s-\omega }{\rm{d}}s\right]\displaystyle \prod _{n=1}^{2N}\frac{\omega -{\overline{\eta }}_{n}}{\omega -{\eta }_{n}},\quad \omega \in {D}^{+}.\end{eqnarray}$
Taking ω → 0, equation (80a ) can be rewritten as
$\begin{eqnarray}{Q}_{0}=-\frac{1}{4\pi }{\int }_{{\rm{\Sigma }}}\frac{\mathrm{log}\left[1-\widetilde{\rho }\left(s\right)\hat{\widetilde{\rho }}\left(s\right)\right]}{s}{\rm{d}}s-2\displaystyle \sum _{n=1}^{N}{\rm{\arg }}\left({\eta }_{n}\right).\end{eqnarray}$
3.2.4. Solution u for the reflectionless case
We now construct the solution u under the reflectionless condition (i.e., $\widetilde{\rho }(\omega )=0$, $\hat{\widetilde{\rho }}(\omega )=0$). By introducing the notation ${r}_{j}\left(x,t;\omega \right)=\frac{{E}_{j}}{\omega -{\eta }_{j}}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{j}\right)}$ (j = 1, …, 2N) and extracting the second component of equations (73 ), we have the algebraic system
$\begin{eqnarray}{\widetilde{\mu }}_{-,22}\left(x,t;{\eta }_{n}\right)={{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right)}-\displaystyle \sum _{k=1}^{2N}{\overline{r}}_{k}\left(x,t;{\overline{\eta }}_{n}\right){\widetilde{\mu }}_{-,21}\left(x,t;{\overline{\eta }}_{k}\right),\end{eqnarray}$
$\begin{eqnarray}{\widetilde{\mu }}_{-,21}\left(x,t;{\overline{\eta }}_{n}\right)=\displaystyle \sum _{j=1}^{2N}{r}_{j}\left(x,t;{\overline{\eta }}_{n}\right){\widetilde{\mu }}_{-,22}\left(x,t;{\eta }_{j}\right),\quad n=1,\ldots ,2N.\end{eqnarray}$
Substituting equation (82b ) into equation (82a ) yields 83 ) can be written into the matrix form KL = P, where $K=I+R=\left({K}_{1},{K}_{2},\cdots \,,{K}_{2N}\right)$. Solving this matrix equation via Cramer's rule leads to ${L}_{n}=\frac{{\rm{\det }}\left({K}_{n}^{{\rm{r}}{\rm{e}}{\rm{p}}}\right)}{{\rm{\det }}\left(K\right)}$, where ${K}_{n}^{{\rm{r}}{\rm{e}}{\rm{p}}}=\left({K}_{1},{K}_{2},\cdots \,,{K}_{n-1},P,{K}_{n+1},\cdots \,,{K}_{2N}\right)$.
$\begin{eqnarray}{\widetilde{\mu }}_{-,22}\left(x,t;{\eta }_{n}\right)={{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right)}-\displaystyle \sum _{k=1}^{2N}\displaystyle \sum _{j=1}^{2N}{\overline{r}}_{k}\left(x,t;{\overline{\eta }}_{n}\right){r}_{j}\left(x,t;{\overline{\eta }}_{k}\right){\widetilde{\mu }}_{-,22}\left(x,t;{\eta }_{j}\right),\quad n=1,\ldots ,2N.\end{eqnarray}$
Introducing $\begin{eqnarray*}\begin{array}{rcl}{\boldsymbol{L}} & = & {\left({L}_{1},{L}_{2},\cdots \,,{L}_{2N}\right)}^{{\rm{T}}},\quad {L}_{n}={\widetilde{\mu }}_{-,22}\left(x,t;{\eta }_{n}\right),\quad {\boldsymbol{P}}={\left({P}_{1},{P}_{2},\cdots \,,{P}_{2N}\right)}^{{\rm{T}}},\quad {P}_{n}={{\rm{e}}}^{{\rm{i}}{Q}_{-}\left(x,t\right)},\\ R & = & {\left({R}_{n,j}\right)}_{2N\times 2N},\quad {R}_{n,j}=\displaystyle \sum _{k=1}^{2N}{\overline{r}}_{k}\left(x,t;{\overline{\eta }}_{n}\right){r}_{j}\left(x,t;{\overline{\eta }}_{k}\right),\end{array}\end{eqnarray*}$
equation (Finally, substituting Ln into the reconstruction formula (75 ), the solution u can be obtained in the form of determinants
$\begin{eqnarray}u=\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}{{\rm{e}}}^{2{\rm{i}}{Q}_{-}\left(x,t\right)},\end{eqnarray}$
where the (2N + 1) × (2N + 1) matrix Kaug is given by $\begin{eqnarray*}{K}^{{\rm{a}}{\rm{u}}{\rm{g}}}=\left(\begin{array}{cc}0 & X\\ {\boldsymbol{1}} & K\end{array}\right),\quad X=\left({X}_{1},{X}_{2},\cdots \,,{X}_{2N}\right),\quad {X}_{n}={E}_{n}{{\rm{e}}}^{-2{\rm{i}}\widetilde{\theta }\left(x,t;{\eta }_{n}\right)}.\end{eqnarray*}$
4. Soliton solutions and asymptotic analysis
Based on equations (61 ) and (84 ), the explicit expressions of ${\left|u\right|}^{2}$ and ${\left|v\right|}^{2}$ can be obtained. Then, we substitute them into the integration in equation (22 ) and derive the explicit N-soliton solutions of system (2) as follows:
$\begin{eqnarray}u=\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}{\rm{\exp }}\left[\frac{{\rm{i}}}{2}{\int }_{-\infty }^{x}\left({\left|\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}\right|}^{2}+{\left|\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}\right|}^{2}\right){\rm{d}}y\right],\end{eqnarray}$
$\begin{eqnarray}v=\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}{\rm{\exp }}\left[-\frac{{\rm{i}}}{2}{\int }_{-\infty }^{x}\left({\left|\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}\right|}^{2}+{\left|\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}\right|}^{2}\right){\rm{d}}y\right].\end{eqnarray}$
The first conservation law of system (2) can be derived as 85 ) combining with equation (86 ) into system (2), we can obtain the explicit expression about the integral, i.e.,
$\begin{eqnarray}{\left({\left|u\right|}^{2}+{\left|v\right|}^{2}\right)}_{t}={\left({\left|v\right|}^{2}-{\left|u\right|}^{2}\right)}_{x}.\end{eqnarray}$
By substituting solutions ( $\begin{eqnarray}{\int }_{-\infty }^{x}\left({\left|u\right|}^{2}+{\left|v\right|}^{2}\right){\rm{d}}y={\rm{\arctan }}\left\{\frac{\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}{\kappa }_{2}-\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}{\kappa }_{1}}{{\rm{i}}\left[\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}{\kappa }_{2}+\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}{\kappa }_{1}\right]}\right\}+C,\end{eqnarray}$
where ${\kappa }_{1}={\rm{i}}\left[{\left(\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}\right)}_{x}+{\left(\frac{{\rm{\det }}\left({K}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(K\right)}\right)}_{t}\right]$, ${\kappa }_{2}={\rm{i}}\left[{\left(\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}\right)}_{t}-{\left(\frac{{\rm{\det }}\left({H}^{{\rm{a}}{\rm{u}}{\rm{g}}}\right)}{{\rm{\det }}\left(H\right)}\right)}_{x}\right]$ and C is a real number.In the following, we will study the dynamical properties of one-soliton and two-soliton solutions as special cases of solution (85 ).
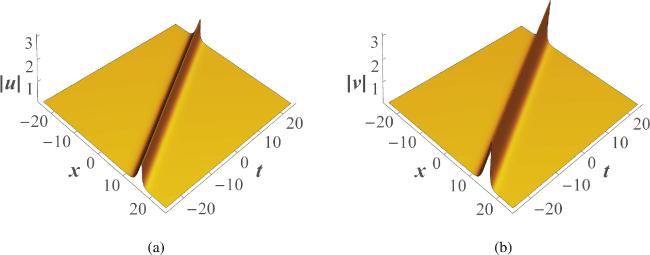
4.1. One-soliton solutions
By setting N = 1 in equations (85 ), the one-soliton solutions of system (2) are presented as follows:
$\begin{eqnarray}u=\frac{\frac{2{b}_{1}}{\left|{b}_{1}\right|}{\rm{\exp }}\left\{2{\rm{i}}\left[-{\theta }_{1{\rm{R}}}-{{\rm{\Phi }}}_{1}+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}\right)\right]\right\}}{{\left|{\xi }_{1}\right|}^{2}\left[\frac{1}{{\xi }_{1{\rm{R}}}}{\rm{\sinh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)-{\rm{i}}\frac{1}{{\xi }_{1{\rm{I}}}}{\rm{\cosh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right]},\end{eqnarray}$
$\begin{eqnarray}v=\frac{\frac{2{b}_{1}}{\left|{b}_{1}\right|}{\rm{\exp }}\left\{2{\rm{i}}\left[-{\theta }_{1{\rm{R}}}+{{\rm{\Phi }}}_{1}-{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right)-{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}\right)\right]\right\}}{\frac{1}{{\xi }_{1{\rm{R}}}}{\rm{\sinh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)+{\rm{i}}\frac{1}{{\xi }_{1{\rm{I}}}}{\rm{\cosh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)},\end{eqnarray}$
with
$\begin{eqnarray*}\begin{array}{rcl}{\theta }_{1{\rm{R}}} & = & \frac{{\xi }_{1{\rm{R}}}^{2}-{\xi }_{1{\rm{I}}}^{2}}{4{\left|{\xi }_{1}\right|}^{4}}\left[\left({\left|{\xi }_{1}\right|}^{4}-1\right)x+\left({\left|{\xi }_{1}\right|}^{4}+1\right)t\right],\\ {\theta }_{1{\rm{I}}} & = & \frac{{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}}{2{\left|{\xi }_{1}\right|}^{4}}\left[\left({\left|{\xi }_{1}\right|}^{4}+1\right)x+\left({\left|{\xi }_{1}\right|}^{4}-1\right)t\right],\end{array}\end{eqnarray*}$
where ξ1 is an eigenvalue selected in the region D+, b1 is an arbitrary nonzero constant in ${\mathbb{C}}$, ${\theta }_{1}=\theta \left(x,t;{\xi }_{1}\right)$ and ${{\rm{\Phi }}}_{1}={\rm{\arg }}\left({\xi }_{1}\right)$, the subscripts 'R' and 'I' denote the real and imaginary parts of the function or argument, respectively.To analyze the properties of one-soliton solutions, we write the square modulus of u and v in the hyperbolic-function form:
$\begin{eqnarray}{\left|u\right|}^{2}=\frac{8{\xi }_{1{\rm{R}}}^{2}{\xi }_{1{\rm{I}}}^{2}}{{\left|{\xi }_{1}\right|}^{4}\left\{{\left|{\xi }_{1}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right]+{\rm{Re}}\left({\xi }_{1}^{2}\right)\right\}},\end{eqnarray}$
$\begin{eqnarray}{\left|v\right|}^{2}=\frac{8{\xi }_{1{\rm{R}}}^{2}{\xi }_{1{\rm{I}}}^{2}}{{\left|{\xi }_{1}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right]+{\rm{Re}}\left({\xi }_{1}^{2}\right)}.\end{eqnarray}$
For the components u and v, the soliton velocities are the same i.e., $V=\frac{1-{\left|{\xi }_{1}\right|}^{4}}{{\left|{\xi }_{1}\right|}^{4}+1}$, and the center trajectories are also the same, i.e., ${ \mathcal C }:2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|=0$. Meanwhile, the amplitudes in the two components are ${A}_{u}=\frac{2{\xi }_{1{\rm{I}}}}{{\left|{\xi }_{1}\right|}^{2}}$ and Av = 2ξ1I, respectively. With ξ1 = 1 + i and b1 = 1 + i in solutions (88 ), figure 2 shows that both the u and v components display the bright one-soliton profiles.
Figure 2. 3D plots of the one-soliton solutions ( |
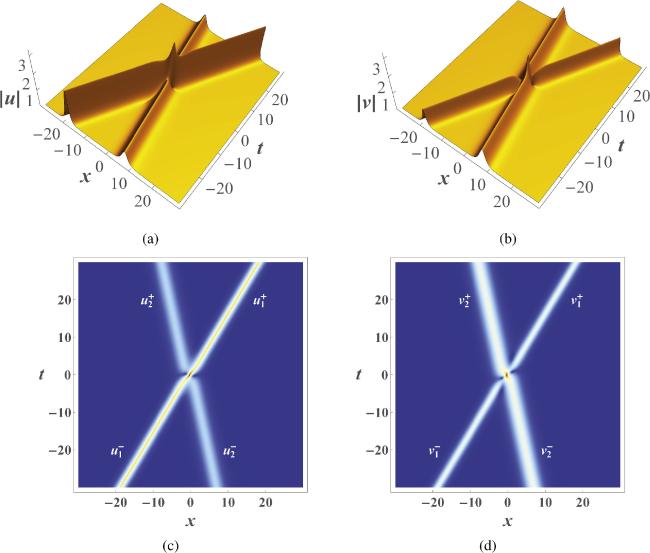
Figure 3. (a) and (b): 3D plots of the two-soliton solutions in the components u and v with ${\xi }_{1}=\frac{1}{2}+\frac{1}{2}{\rm{i}}$, ${\xi }_{2}=1+\frac{1}{2}{\rm{i}}$, b1 = 1 + i and b2 = 1 + i; (c) and (d): Density plots of (a) and (b). |
4.2. Two-soliton solutions
When N = 2 in equations (85 ), the two-soliton solutions are derived as follows:
$\begin{eqnarray}u={u}_{1}{\rm{\exp }}\left[\frac{{\rm{i}}}{2}{\int }_{-\infty }^{x}\left({\left|{u}_{1}\right|}^{2}+{\left|{v}_{1}\right|}^{2}\right){\rm{d}}y\right],\end{eqnarray}$
$\begin{eqnarray}v={v}_{1}{\rm{\exp }}\left[-\frac{{\rm{i}}}{2}{\int }_{-\infty }^{x}\left({\left|{u}_{1}\right|}^{2}+{\left|{v}_{1}\right|}^{2}\right){\rm{d}}y\right],\end{eqnarray}$
with
$\begin{eqnarray*}\begin{array}{rcl}{u}_{1} & = & \frac{-{{\rm{e}}}^{-2{\rm{i}}\left({{\rm{\Phi }}}_{1}+{{\rm{\Phi }}}_{2}\right)}\left[\frac{{b}_{1}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{1{\rm{R}}}}}{{\overline{\xi }}_{1}}\left(\frac{{\xi }_{2}{\overline{\alpha }}_{1}{{\rm{e}}}^{-2{\rm{i}}{\overline{\theta }}_{2}}}{{\overline{\xi }}_{2}}-{\left|{b}_{2}\right|}^{2}{\alpha }_{1}{{\rm{e}}}^{-2{\rm{i}}{\theta }_{2}}\right)+\frac{{b}_{2}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{2{\rm{R}}}}}{{\overline{\xi }}_{2}}\left({\left|{b}_{1}\right|}^{2}{\overline{\alpha }}_{2}{{\rm{e}}}^{-2{\rm{i}}{\theta }_{1}}-\frac{{\xi }_{1}{\alpha }_{2}{{\rm{e}}}^{-2{\rm{i}}{\overline{\theta }}_{1}}}{{\overline{\xi }}_{1}}\right)\right]}{{{\rm{e}}}^{-2{\rm{i}}\left({\overline{\theta }}_{1}+{\overline{\theta }}_{2}\right)}+{\xi }_{1}{b}_{1}\left(\frac{{\overline{b}}_{2}{\gamma }_{1}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{1{\rm{R}}}}}{{\overline{\xi }}_{2}}+\frac{{\overline{b}}_{1}{\gamma }_{2}{{\rm{e}}}^{-2{\rm{i}}\left({\overline{\theta }}_{2}+{\theta }_{1}\right)}}{{\overline{\xi }}_{1}}\right)+{\xi }_{2}{b}_{2}\left(\frac{{\overline{b}}_{1}{\gamma }_{1}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{2{\rm{R}}}}}{{\overline{\xi }}_{1}}+\frac{{\overline{b}}_{2}{\gamma }_{2}{{\rm{e}}}^{-2{\rm{i}}\left({\overline{\theta }}_{1}+{\theta }_{2}\right)}}{{\overline{\xi }}_{2}}\right)+{\overline{\gamma }}_{3}{{\rm{e}}}^{-2{\rm{i}}\left({\theta }_{1}+{\theta }_{2}\right)}},\\ {v}_{1} & = & \frac{{{\rm{e}}}^{2{\rm{i}}\left({{\rm{\Phi }}}_{1}+{{\rm{\Phi }}}_{2}\right)}\left[{\overline{\xi }}_{1}{b}_{1}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{1{\rm{R}}}}\left(\frac{{\overline{\xi }}_{2}{\overline{\alpha }}_{1}{{\rm{e}}}^{-2{\rm{i}}{\overline{\theta }}_{2}}}{{\xi }_{2}}-{\left|{b}_{2}\right|}^{2}{\alpha }_{1}{{\rm{e}}}^{-2{\rm{i}}{\theta }_{2}}\right)+{\overline{\xi }}_{2}{b}_{2}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{2{\rm{R}}}}\left({\left|{b}_{1}\right|}^{2}{\overline{\alpha }}_{2}{{\rm{e}}}^{-2{\rm{i}}{\theta }_{1}}-\frac{{\overline{\xi }}_{1}{\alpha }_{2}{{\rm{e}}}^{-2{\rm{i}}{\overline{\theta }}_{1}}}{{\xi }_{1}}\right)\right]}{{{\rm{e}}}^{-2{\rm{i}}\left({\overline{\theta }}_{1}+{\overline{\theta }}_{2}\right)}+\frac{{b}_{1}}{{\xi }_{1}}\left({\overline{\xi }}_{2}{\overline{b}}_{2}{\gamma }_{1}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{1{\rm{R}}}}+{\overline{\xi }}_{1}{\overline{b}}_{1}{\gamma }_{2}{{\rm{e}}}^{-2{\rm{i}}\left({\overline{\theta }}_{2}+{\theta }_{1}\right)}\right)+\frac{{b}_{2}}{{\xi }_{2}}\left({\overline{\xi }}_{1}{\overline{b}}_{1}{\gamma }_{1}{{\rm{e}}}^{-4{\rm{i}}{\theta }_{2{\rm{R}}}}+{\overline{\xi }}_{2}{\overline{b}}_{2}{\gamma }_{2}{{\rm{e}}}^{-2{\rm{i}}\left({\overline{\theta }}_{1}+{\theta }_{2}\right)}\right)+\frac{{\overline{\xi }}_{1}^{2}{\overline{\xi }}_{2}^{2}{\overline{\gamma }}_{3}}{{\xi }_{1}^{2}{\xi }_{2}^{2}}{{\rm{e}}}^{-2{\rm{i}}\left({\theta }_{1}+{\theta }_{2}\right)}},\\ {\alpha }_{1} & = & \frac{2{\rm{i}}\left({\xi }_{2}^{2}-{\overline{\xi }}_{1}^{2}\right){\rm{Im}}({\overline{\xi }}_{1}^{2}){\overline{\xi }}_{2}}{\left({\overline{\xi }}_{1}^{2}-{\overline{\xi }}_{2}^{2}\right){\left|{\xi }_{1}\right|}^{2}{\xi }_{2}},\\ {\alpha }_{2} & = & \frac{2{\rm{i}}\left({\overline{\xi }}_{1}^{2}-{\xi }_{2}^{2}\right){\rm{Im}}({\xi }_{2}^{2}){\xi }_{1}}{({\xi }_{1}^{2}-{\xi }_{2}^{2}){\left|{\xi }_{2}\right|}^{2}{\overline{\xi }}_{1}},\\ {\gamma }_{1} & = & \frac{4{\rm{Im}}({\overline{\xi }}_{1}^{2}){\rm{Im}}({\xi }_{2}^{2})}{{\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}^{2}},\\ {\gamma }_{2} & = & \frac{{\left|{\overline{\xi }}_{1}^{2}-{\xi }_{2}^{2}\right|}^{2}}{{\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}^{2}},\\ {\gamma }_{3} & = & \frac{{\overline{\xi }}_{1}{\overline{\xi }}_{2}{\left|{b}_{1}\right|}^{2}{\left|{b}_{2}\right|}^{2}}{{\xi }_{1}{\xi }_{2}},\\ {\theta }_{2{\rm{R}}} & = & \frac{{\xi }_{2{\rm{R}}}^{2}-{\xi }_{2{\rm{I}}}^{2}}{4{\left|{\xi }_{2}\right|}^{4}}\left[\left({\left|{\xi }_{2}\right|}^{4}-1\right)x+\left({\left|{\xi }_{2}\right|}^{4}+1\right)t\right],\end{array}\end{eqnarray*}$
where ξ1 and ξ2 are eigenvalues both selected in the region D+, b1 and b2 are two arbitrary nonzero constants in ${\mathbb{C}}$, ${\theta }_{1}=\theta \left(x,t;{\xi }_{1}\right)$, ${\theta }_{2}=\theta \left(x,t;{\xi }_{2}\right)$, ${{\rm{\Phi }}}_{1}={\rm{\arg }}\left({\xi }_{1}\right)$ and ${{\rm{\Phi }}}_{2}={\rm{\arg }}\left({\xi }_{2}\right)$.In order to reveal the interaction properties of two-soliton solutions, we derive all the asymptotic solitons of solutions (90) as ∣t∣ → ∞. Without loss of generality, we assume that $\left|{\xi }_{1}\right|\lt \left|{\xi }_{2}\right|$. From the difference
$\begin{eqnarray*}2{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}\left(1+\frac{1}{{\left|{\xi }_{2}\right|}^{4}}\right){\theta }_{1{\rm{I}}}-2{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}\left(1+\frac{1}{{\left|{\xi }_{1}\right|}^{4}}\right){\theta }_{2{\rm{I}}}={\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}\frac{2\left({\left|{\xi }_{1}\right|}^{4}-{\left|{\xi }_{2}\right|}^{4}\right)}{{\left|{\xi }_{1}\right|}^{4}{\left|{\xi }_{2}\right|}^{4}}t,\end{eqnarray*}$
with ${\theta }_{2{\rm{I}}}=\frac{{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}}{2{\left|{\xi }_{2}\right|}^{4}}\left[\left({\left|{\xi }_{2}\right|}^{4}+1\right)x+\left({\left|{\xi }_{2}\right|}^{4}-1\right)t\right]$, it is easy to find that if ${\theta }_{1{\rm{I}}}={ \mathcal O }\left(1\right)$, θ2I → ± ∞ as t → ± ∞; if ${\theta }_{2{\rm{I}}}={ \mathcal O }\left(1\right)$, θ1I → ∓ ∞ as t → ± ∞. Thus, one can obtain four pairs of asymptotic solitons ${u}_{i}^{\pm }$ and ${v}_{i}^{\pm }$ $\left(i=1,2\right)$, where the superscripts '+' and '-' correspond to t → ± ∞, respectively. Figure 4 shows that the asymptotic expressions agree well with the exact solutions (90), which confirms the validity of our asymptotic analysis.
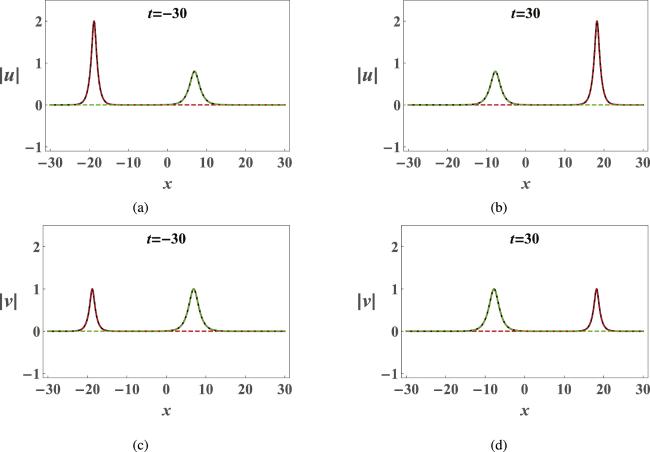
Figure 4. Comparison of the asymptotic solitons ${u}_{j}^{\pm }$ and ${v}_{j}^{\pm }$ ( red and green dashed for j = 1 and j = 2, respectively) with the exact solutions (black solid) at different t with ${\xi }_{1}=\frac{1}{2}+\frac{1}{2}{\rm{i}}$, ${\xi }_{2}=1+\frac{1}{2}{\rm{i}}$, b1 = 1 + i and b2 = 1 + i. |
Case 1: ${\theta }_{1{\rm{I}}}={ \mathcal O }\left(1\right)$ and t → + ∞.
$\begin{eqnarray}\begin{array}{rcl}{u}_{1}^{+} & = & \frac{-2{\rm{i}}{b}_{1}{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}\left({\xi }_{1}^{2}-{\xi }_{2}^{2}\right)\left({\xi }_{2}^{2}-{\overline{\xi }}_{1}^{2}\right){\overline{\xi }}_{2}^{2}}{{\tau }_{1}^{+}\left|{b}_{1}\right|\left[{\rm{\cosh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)+{\rm{i}}\frac{{\rm{Im}}\left({\xi }_{1}{\xi }_{2}^{2}\right)}{{\rm{Re}}\left({\xi }_{1}{\xi }_{2}^{2}\right)}{\rm{\sinh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right]+{\overline{\zeta }}_{1}^{+}{\rm{\exp }}\left(-2{\theta }_{1{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}-{\theta }_{1{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}(| {b}_{1}| \Upsilon )\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{v}_{1}^{+} & = & \frac{-2{\rm{i}}{b}_{1}{\xi }_{1{\rm{I}}}\left({\xi }_{1}^{2}-{\xi }_{2}^{2}\right)\left({\overline{\xi }}_{1}^{2}-{\xi }_{2}^{2}\right)}{{\chi }_{1}^{+}\left|{b}_{1}\right|\left[{\rm{\cosh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)-{\rm{i}}\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}{\rm{\sinh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right]+{\overline{\pi }}_{1}^{+}{\rm{\exp }}\left(-2{\theta }_{1{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{-2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}+{\theta }_{1{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}(| {b}_{1}| \Upsilon )\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
and the corresponding intensities are
$\begin{eqnarray}{\left|{u}_{1}^{+}\right|}^{2}=\frac{8{\xi }_{1{\rm{R}}}^{2}{\xi }_{1{\rm{I}}}^{2}}{{\left|{\xi }_{1}\right|}^{4}\left\{{\left|{\xi }_{1}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}(| {b}_{1}| \Upsilon )\right)\right]+{\rm{Re}}\left({\xi }_{1}^{2}\right)\right\}},\end{eqnarray}$
$\begin{eqnarray}{\left|{v}_{1}^{+}\right|}^{2}=\frac{8{\xi }_{1{\rm{R}}}^{2}{\xi }_{1{\rm{I}}}^{2}}{{\left|{\xi }_{1}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}(| {b}_{1}| \Upsilon )\right)\right]+{\rm{Re}}\left({\xi }_{1}^{2}\right)},\end{eqnarray}$
where
$\begin{eqnarray*}\begin{array}{rcl}{\tau }_{1}^{+} & = & {\left|{\xi }_{1}\right|}^{2}{\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}^{2}{\rm{Re}}\left({\xi }_{1}{\xi }_{2}^{2}\right),\quad {\zeta }_{1}^{+}=2{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}{\left|{\xi }_{1}\right|}^{2}\left({\xi }_{1{\rm{I}}}{\left|{\left|{\xi }_{1}\right|}^{2}+{\xi }_{2}^{2}\right|}^{2}-{\rm{i}}{\xi }_{1{\rm{R}}}{\left|{\left|{\xi }_{1}\right|}^{2}-{\xi }_{2}^{2}\right|}^{2}\right),\\ {\chi }_{1}^{+} & = & {\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}^{2},\quad {\pi }_{1}^{+}=8{\xi }_{1{\rm{I}}}{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}{\overline{\xi }}_{1},\quad \Upsilon =\frac{\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}{\left|{\overline{\xi }}_{1}^{2}-{\xi }_{2}^{2}\right|}.\end{array}\end{eqnarray*}$
Case 2: ${\theta }_{1{\rm{I}}}={ \mathcal O }\left(1\right)$ and t → − ∞.
$\begin{eqnarray}\begin{array}{rcl}{u}_{1}^{-} & = & \frac{-2{\rm{i}}{b}_{1}{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}\left({\xi }_{1}^{2}-{\overline{\xi }}_{2}^{2}\right)\left({\overline{\xi }}_{2}^{2}-{\overline{\xi }}_{1}^{2}\right){\xi }_{2}^{2}}{{\tau }_{1}^{-}\left|{b}_{1}\right|\left[{\rm{\cosh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)-{\rm{i}}\frac{{\rm{Im}}\left({\overline{\xi }}_{1}{\xi }_{2}^{2}\right)}{{\rm{Re}}\left({\overline{\xi }}_{1}{\xi }_{2}^{2}\right)}{\rm{\sinh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right]+{\overline{\zeta }}_{1}^{+}{\rm{\exp }}\left(-2{\theta }_{1{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}-{\theta }_{1{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{1}\right|}{\Upsilon }\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{v}_{1}^{-} & = & \frac{-2{\rm{i}}{b}_{1}{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}{\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}^{2}\left({\xi }_{1}^{2}-{\overline{\xi }}_{2}^{2}\right){\xi }_{1}}{{\chi }_{1}^{-}\left|{b}_{1}\right|\left[{\rm{\cosh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)-{\rm{i}}\frac{{\rm{Im}}({\xi }_{1}^{2})-{\rm{Im}}({\xi }_{2}^{2})}{{\rm{Re}}({\xi }_{1}^{2})-{\rm{Re}}({\xi }_{2}^{2})}{\rm{\sinh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\left|{b}_{1}\right|\right)\right]+{\overline{\pi }}_{1}^{-}{\rm{\exp }}\left(-2{\theta }_{1{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{-2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}+{\theta }_{1{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{1}\right|}{\Upsilon }\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{1{\rm{I}}}}{{\xi }_{1{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
and the corresponding intensities are
$\begin{eqnarray}{\left|{u}_{1}^{-}\right|}^{2}=\frac{8{\xi }_{1{\rm{R}}}^{2}{\xi }_{1{\rm{I}}}^{2}}{{\left|{\xi }_{1}\right|}^{4}\left\{{\left|{\xi }_{1}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{1}\right|}{\Upsilon }\right)\right]+{\rm{Re}}\left({\xi }_{1}^{2}\right)\right\}},\end{eqnarray}$
$\begin{eqnarray}{\left|{v}_{1}^{-}\right|}^{2}=\frac{8{\xi }_{1{\rm{R}}}^{2}{\xi }_{1{\rm{I}}}^{2}}{{\left|{\xi }_{1}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{1{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{1}\right|}{\Upsilon }\right)\right]+{\rm{Re}}\left({\xi }_{1}^{2}\right)},\end{eqnarray}$
where
$\begin{eqnarray*}\begin{array}{rcl}{\tau }_{1}^{-} & = & -{\left|{\xi }_{1}\right|}^{2}{\left|{\xi }_{1}^{2}-{\overline{\xi }}_{2}^{2}\right|}^{2}{\rm{Re}}\left({\overline{\xi }}_{1}{\xi }_{2}^{2}\right),\quad {\chi }_{1}^{-}={\left|{\xi }_{1}\right|}^{2}{\left|{\xi }_{1}^{2}-{\overline{\xi }}_{2}^{2}\right|}^{2}\left[{\rm{Re}}({\xi }_{1}^{2})-{\rm{Re}}({\xi }_{2}^{2})\right],\\ {\pi }_{1}^{-} & = & {\xi }_{1{\rm{I}}}\left\{2{\left|{\xi }_{1}\right|}^{2}\left[{\rm{Re}}\left({\xi }_{1}^{3}\right){\rm{Im}}\left({\overline{\xi }}_{2}^{2}\right)+{\left|{\xi }_{1}\right|}^{2}{\rm{Im}}\left({\xi }_{1}\right){\rm{Re}}\left({\xi }_{2}^{2}\right)\right]+{\rm{Im}}\left[{\overline{\xi }}_{1}^{3}\left({\left|{\xi }_{1}\right|}^{4}+2{\left|{\xi }_{2}\right|}^{4}\right)\right.\right.\\ & & \left.\left.+{\xi }_{1}\left({\left|{\xi }_{1}\right|}^{2}{\xi }_{2}^{4}+{\xi }_{1}^{4}{\overline{\xi }}_{2}^{2}+{\left|{\xi }_{2}\right|}^{4}{\xi }_{2}^{2}\right)\right]\right\}+\frac{{\rm{i}}}{2}\left\{{\rm{Im}}\left[{\left|{\xi }_{1}\right|}^{4}\left({\left|{\xi }_{1}\right|}^{2}{\overline{\xi }}_{1}^{2}+{\overline{\xi }}_{1}^{4}+{\overline{\xi }}_{2}^{4}+2{\xi }_{1}^{2}{\xi }_{2}^{2}\right)+{\xi }_{1}^{4}\left({\left|{\xi }_{1}\right|}^{2}{\xi }_{2}^{2}+{\xi }_{1}^{2}{\overline{\xi }}_{2}^{2}\right)\right.\right.\\ & & \left.\left.+{\left|{\xi }_{2}\right|}^{4}\left(2{\overline{\xi }}_{1}^{4}+{\xi }_{1}^{2}{\xi }_{2}^{2}\right)\right]+{\left|{\xi }_{1}\right|}^{2}{\overline{\xi }}_{2}^{2}{\rm{Im}}\left({\overline{\xi }}_{1}^{2}{\overline{\xi }}_{2}^{2}\right)+{\left|{\xi }_{1}\right|}^{2}{\xi }_{2}^{2}\left({\xi }_{1}^{2}-{\overline{\xi }}_{2}^{2}\right){\rm{Im}}\left({\overline{\xi }}_{2}^{2}\right)\right\}.\end{array}\end{eqnarray*}$
Case 3: ${\theta }_{2{\rm{I}}}={ \mathcal O }\left(1\right)$ and t → + ∞.
$\begin{eqnarray}\begin{array}{rcl}{u}_{2}^{+} & = & \frac{-2{\rm{i}}{b}_{2}{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}\left({\overline{\xi }}_{2}^{2}-{\overline{\xi }}_{1}^{2}\right)\left({\xi }_{2}^{2}-{\overline{\xi }}_{1}^{2}\right){\xi }_{1}^{2}}{{\tau }_{2}^{+}\left|{b}_{2}\right|\left[{\rm{\cosh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)-{\rm{i}}\frac{{\rm{Im}}\left({\overline{\xi }}_{2}{\xi }_{1}^{2}\right)}{{\rm{Re}}\left({\overline{\xi }}_{2}{\xi }_{1}^{2}\right)}{\rm{\sinh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)\right]+{\overline{\zeta }}_{2}^{+}{\rm{\exp }}\left(-2{\theta }_{2{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}-{\theta }_{2{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{2}\right|}{\Upsilon }\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{v}_{2}^{+} & = & \frac{-2{\rm{i}}{b}_{2}{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}{\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}^{2}\left({\overline{\xi }}_{1}^{2}-{\xi }_{2}^{2}\right){\xi }_{2}}{{\chi }_{2}^{+}\left|{b}_{2}\right|\left[{\rm{\cosh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)-{\rm{i}}\frac{{\rm{Im}}({\xi }_{1}^{2})-{\rm{Im}}({\xi }_{2}^{2})}{{\rm{Re}}({\xi }_{1}^{2})-{\rm{Re}}({\xi }_{2}^{2})}{\rm{\sinh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)\right]+{\overline{\pi }}_{2}^{+}{\rm{\exp }}\left(-2{\theta }_{2{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{-2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}+{\theta }_{2{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{2}\right|}{\Upsilon }\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
and the corresponding intensities are
$\begin{eqnarray}{\left|{u}_{2}^{+}\right|}^{2}=\frac{8{\xi }_{2{\rm{R}}}^{2}{\xi }_{2{\rm{I}}}^{2}}{{\left|{\xi }_{2}\right|}^{4}\left\{{\left|{\xi }_{2}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{2}\right|}{\Upsilon }\right)\right]+{\rm{Re}}\left({\xi }_{2}^{2}\right)\right\}},\end{eqnarray}$
$\begin{eqnarray}{\left|{v}_{2}^{+}\right|}^{2}=\frac{8{\xi }_{2{\rm{R}}}^{2}{\xi }_{2{\rm{I}}}^{2}}{{\left|{\xi }_{2}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{2}\right|}{\Upsilon }\right)\right]+{\rm{Re}}\left({\xi }_{2}^{2}\right)},\end{eqnarray}$
where
$\begin{eqnarray*}\begin{array}{rcl}{\tau }_{2}^{+} & = & -{\left|{\xi }_{2}\right|}^{2}{\left|{\xi }_{1}^{2}-{\overline{\xi }}_{2}^{2}\right|}^{2}{\rm{Re}}\left({\xi }_{1}^{2}{\overline{\xi }}_{2}\right),\quad {\zeta }_{2}^{+}=2{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}{\left|{\xi }_{2}\right|}^{2}\left({\xi }_{2{\rm{I}}}{\left|{\xi }_{1}^{2}+{\left|{\xi }_{2}\right|}^{2}\right|}^{2}-{\rm{i}}{\xi }_{2{\rm{R}}}{\left|{\xi }_{1}^{2}-{\left|{\xi }_{2}\right|}^{2}\right|}^{2}\right),\quad {\chi }_{2}^{+}=\frac{{\left|{\xi }_{2}\right|}^{2}{{\rm{\Delta }}}_{3}}{{\left|{\xi }_{1}\right|}^{2}},\\ {\pi }_{2}^{+} & = & {\rm{Im}}\left({\overline{\xi }}_{2}\right){\rm{Im}}\left\{{\left|{\xi }_{2}\right|}^{2}\left[{\xi }_{1}^{4}{\xi }_{2}+{\overline{\xi }}_{1}^{2}\left({\xi }_{2}^{3}+{\overline{\xi }}_{2}^{3}+{\left|{\xi }_{2}\right|}^{2}{\xi }_{2}\right)+{\left|{\xi }_{2}\right|}^{2}\left({\xi }_{1}^{2}{\xi }_{2}+{\overline{\xi }}_{2}^{3}\right)\right]+{\left|{\xi }_{1}\right|}^{4}\left(2{\overline{\xi }}_{2}^{3}+{\xi }_{1}^{2}{\xi }_{2}\right)+{\overline{\xi }}_{1}^{2}{\xi }_{2}^{5}\right\}\\ & & +\frac{{\rm{i}}}{2}{\rm{Im}}\left\{{\left|{\xi }_{2}\right|}^{2}\left[{\xi }_{1}^{4}{\xi }_{2}^{2}+{\overline{\xi }}_{1}^{2}{\overline{\xi }}_{2}^{4}+{\left|{\xi }_{2}\right|}^{2}\left({\overline{\xi }}_{1}^{4}+{\xi }_{2}^{4}+2{\overline{\xi }}_{1}^{2}{\overline{\xi }}_{2}^{2}+{\left|{\xi }_{2}\right|}^{2}{\xi }_{2}^{2}\right)\right]+{\left|{\xi }_{1}\right|}^{4}\left[2{\xi }_{2}^{4}+{\overline{\xi }}_{1}^{2}\left({\overline{\xi }}_{1}^{2}+{\overline{\xi }}_{2}^{2}+{\left|{\xi }_{2}\right|}^{2}\right)\right]\right\}.\end{array}\end{eqnarray*}$
Case 4: ${\theta }_{2{\rm{I}}}={ \mathcal O }\left(1\right)$ and t → − ∞.
$\begin{eqnarray}\begin{array}{rcl}{u}_{2}^{-} & = & \frac{-2{\rm{i}}{b}_{2}{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}\left({\xi }_{1}^{2}-{\xi }_{2}^{2}\right)\left({\overline{\xi }}_{2}^{2}-{\xi }_{1}^{2}\right){\overline{\xi }}_{1}^{2}}{{\tau }_{2}^{-}\left|{b}_{2}\right|\left[{\rm{\cosh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)-{\rm{i}}\frac{{\rm{Im}}\left({\overline{\xi }}_{1}^{2}{\overline{\xi }}_{2}\right)}{{\rm{Re}}\left({\overline{\xi }}_{1}^{2}{\overline{\xi }}_{2}\right)}{\rm{\sinh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)\right]+{\overline{\zeta }}_{2}^{+}{\rm{\exp }}\left(-2{\theta }_{2{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}-{\theta }_{2{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left(\left|{b}_{2}\right|\Upsilon \right)\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{v}_{2}^{-} & = & \frac{-2{\rm{i}}{b}_{2}{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}\left({\xi }_{1}^{2}-{\overline{\xi }}_{2}^{2}\right)\left({\xi }_{1}^{2}-{\xi }_{2}^{2}\right)}{{\chi }_{2}^{-}\left|{b}_{2}\right|\left[{\xi }_{2{\rm{R}}}{\rm{\cosh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)-{\rm{i}}{\xi }_{2{\rm{I}}}{\rm{\sinh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left|{b}_{2}\right|\right)\right]+{\overline{\pi }}_{2}^{-}{\rm{\exp }}\left(-2{\theta }_{2{\rm{I}}}\right)}\\ & & \times {\rm{\exp }}\left\{-2{\rm{i}}\left[-{{\rm{\Phi }}}_{1}-{{\rm{\Phi }}}_{2}+{\theta }_{2{\rm{R}}}+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}{\rm{\tanh }}\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left(\left|{b}_{2}\right|\Upsilon \right)\right)\right)+{\rm{\arctan }}\left(\frac{{\xi }_{2{\rm{I}}}}{{\xi }_{2{\rm{R}}}}\right)\right]\right\},\end{array}\end{eqnarray}$
and the corresponding intensities are
$\begin{eqnarray}{\left|{u}_{2}^{-}\right|}^{2}=\frac{8{\xi }_{2{\rm{R}}}^{2}{\xi }_{2{\rm{I}}}^{2}}{{\left|{\xi }_{2}\right|}^{4}\left\{{\left|{\xi }_{2}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left(\left|{b}_{2}\right|\Upsilon \right)\right)\right]+{\rm{Re}}\left({\xi }_{2}^{2}\right)\right\}},\end{eqnarray}$
$\begin{eqnarray}{\left|{v}_{2}^{-}\right|}^{2}=\frac{8{\xi }_{2{\rm{R}}}^{2}{\xi }_{2{\rm{I}}}^{2}}{{\left|{\xi }_{2}\right|}^{2}{\rm{\cosh }}\left[2\left(2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left(\left|{b}_{2}\right|\Upsilon \right)\right)\right]+{\rm{Re}}\left({\xi }_{2}^{2}\right)},\end{eqnarray}$
where ${\tau }_{2}^{-}={\left|{\xi }_{2}\right|}^{2}{\left|{\xi }_{1}^{2}-{\xi }_{2}^{2}\right|}^{2}{\rm{Re}}\left({\overline{\xi }}_{1}^{2}{\overline{\xi }}_{2}\right)$, ${\chi }_{2}^{-}=\frac{{{\rm{\Delta }}}_{1}}{{\xi }_{1{\rm{R}}}}$, ${\pi }_{2}^{-}=8{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}{\overline{\xi }}_{2}$.The expressions (92), (94), (96) and (98) show that the asymptotic solitons ${u}_{i}^{\pm }$ and ${v}_{i}^{\pm }$ $\left(i=1,2\right)$ are all of the bright type. The amplitudes and velocities for asymptotic solitons can be explicitly given by
$\begin{eqnarray*}\begin{array}{rcl}{A}_{1,u}^{+} & = & {A}_{1,u}^{-}=\frac{2{\xi }_{1{\rm{I}}}}{{\left|{\xi }_{1}\right|}^{2}},\quad {A}_{1,v}^{+}={A}_{1,v}^{-}=2{\xi }_{1{\rm{I}}},\quad {A}_{2,u}^{+}={A}_{2,u}^{-}=\frac{2{\xi }_{2{\rm{I}}}}{{\left|{\xi }_{2}\right|}^{2}},\quad {A}_{2,v}^{+}={A}_{2,v}^{-}=2{\xi }_{2{\rm{I}}},\\ {V}_{1,u}^{\pm } & = & {V}_{1,v}^{\pm }=\frac{1-{\left|{\xi }_{1}\right|}^{4}}{{\left|{\xi }_{1}\right|}^{4}+1},\quad {V}_{2,u}^{\pm }={V}_{2,v}^{\pm }=\frac{1-{\left|{\xi }_{2}\right|}^{4}}{{\left|{\xi }_{2}\right|}^{4}+1},\end{array}\end{eqnarray*}$
which indicates that the soliton amplitudes and velocities are retained before and after interaction. Meanwhile, the u and v components share the same soliton center trajectories ${{ \mathcal C }}_{i}^{\pm }$ $\begin{eqnarray*}\begin{array}{rcl}{{ \mathcal C }}_{1}^{+}:2{\theta }_{1{\rm{I}}}+{\rm{ln}}(| {b}_{1}| \Upsilon ) & = & 0,\quad {{ \mathcal C }}_{1}^{-}:2{\theta }_{1{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{1}\right|}{\Upsilon }=0,\\ {{ \mathcal C }}_{2}^{+}:2{\theta }_{2{\rm{I}}}+{\rm{ln}}\frac{\left|{b}_{2}\right|}{\Upsilon } & = & 0,\quad {{ \mathcal C }}_{2}^{-}:2{\theta }_{2{\rm{I}}}+{\rm{ln}}\left(\left|{b}_{2}\right|\Upsilon \right)=0,\end{array}\end{eqnarray*}$
so that the two interacting solitons diverge from each other linearly as $\left|t\right|\to \infty $ and there is no interaction force. Besides, the position shifts δφi between $\left({u}_{i}^{+},{v}_{i}^{+}\right)$ and $\left({u}_{i}^{-},{v}_{i}^{-}\right)$ $\left(i=1,2\right)$ upon interaction can be derived as: $\begin{eqnarray*}\delta {\phi }_{1}=\frac{{\left|{\xi }_{1}\right|}^{4}\left[{\rm{ln}}(| {b}_{1}| \Upsilon )-{\rm{ln}}\frac{\left|{b}_{1}\right|}{\Upsilon }\right]}{{\xi }_{1{\rm{R}}}{\xi }_{1{\rm{I}}}\left({\left|{\xi }_{1}\right|}^{4}+1\right)},\quad \delta {\phi }_{2}=\frac{{\left|{\xi }_{2}\right|}^{4}\left[{\rm{ln}}\frac{\left|{b}_{2}\right|}{\Upsilon }-{\rm{ln}}\left(\left|{b}_{2}\right|\Upsilon \right)\right]}{{\xi }_{2{\rm{R}}}{\xi }_{2{\rm{I}}}\left({\left|{\xi }_{2}\right|}^{4}+1\right)}.\end{eqnarray*}$
Therefore, the solutions (90) can describe the standard elastic two-soliton interactions. By setting ${\xi }_{1}=\frac{1}{2}+\frac{1}{2}{\rm{i}}$, ${\xi }_{2}=1+\frac{1}{2}{\rm{i}}$, b1 = 1 + i and b2 = 1 + i in solutions (90), figure 3 displays the elastic interactions between two solitons in the components u and v.4.3. Bound-state solutions
As the special case of two-soliton solutions (90), the bounded states could be obtained by setting $\left|{\xi }_{1}\right|=\left|{\xi }_{2}\right|$ but ξ1 ≠ ξ2, where the two solitons have the same velocities. Note that the relative positions of two interacting solitons are related to the parameters b1 and b2, which will further influence the strength of interaction in the bounded states. In the following, we discuss three different types of two-soliton bounded states, as seen in figure 5.
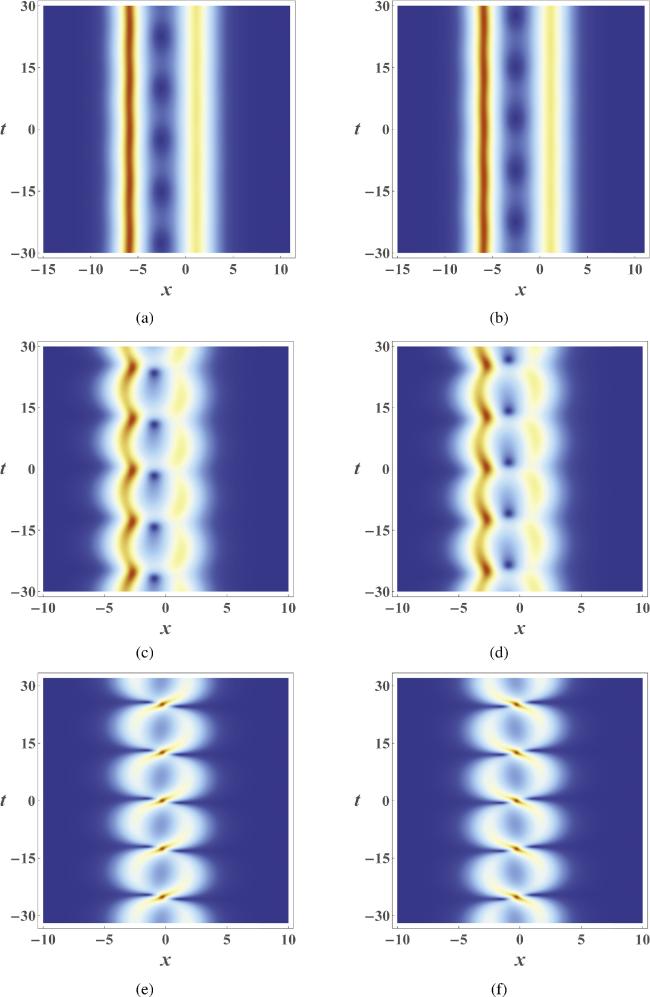
(i) If $\left|\left|{b}_{1}\right|-\left|{b}_{2}\right|\right|\gg 0$, the two solitons are well separated and their relative distance changes very little as the time evolves, so that the interaction force is quite weak (see figures 5(a) and 5(b)).
(ii) If $\left|\left|{b}_{1}\right|-\left|{b}_{2}\right|\right|\gt 0$, the relative distance between two solitons changes periodically but it will not decrease to 0, which means that they never collide at one point (see figures 5(c) and 5(d)).
(iii) If $\left|{b}_{1}\right|=\left|{b}_{2}\right|$, the two solitons collide periodically and form a series of transient waves with large amplitudes at interaction points, so that the strength of soliton interaction is strong, as shown in figures 5(e) and 5(f).
Figure 5. Density plots for three different two-soliton bound states in the components u (left figures) and v (right figures), where the parameters are selected as: ${\xi }_{1}=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}{\rm{i}}$, ${\xi }_{2}=\frac{\sqrt{3}}{2}+\frac{1}{2}{\rm{i}}$, and b1 = 70 + 70i and b2 = 1 + i for (a) and (b); b1 = 4 + 4i and b2 = 1 + i for (c) and (d); b1 = 1 + i and b2 = 1 + i for (e) and (f). |
5. Concluding remarks
In this paper, we have studied the MTM system in laboratory coordinates based on the RH approach when the scattering coefficients have simple zeros. We performed the analysis on the direct scattering including the analyticity, symmetries and asymptotic behaviors of the Jost solutions as ∣λ∣ → ∞ and λ → 0. We have derived the matrix RH problem, reconstruction formulas and trace formulas. Under the reflectionless condition, we have obtained the explicit N-soliton solutions of system (2) in the form of determinants.
As the special cases of N-soliton solutions, the explicit one-soliton solutions in two components u and v have been given. Besides, the propagation properties of one-soliton solutions have been analyzed such as the velocities, center positions and amplitudes. For the two-soliton solutions, we have given the expressions of asymptotic solitons as ∣t∣ → ∞ via the asymptotic analysis method and obtained soliton velocities, amplitudes and position shifts. Through the quantitative analysis on the asymptotic solitons, it turns out that the soliton interactions in two components are elastic and only the position shifts happen after the interaction. Moreover, the asymptotic soliton center trajectories are all along the straight lines which indicate that there is no interaction force between two solitons. By comparing with the exact two-soliton solutions, the asymptotic expressions can describe the behaviors of two solitons well at large ∣t∣. In addition, the two-soliton bound states of system (2) can be derived under the condition $\left|{\xi }_{1}\right|=\left|{\xi }_{2}\right|$ but ${\xi }_{1}\ne {\xi }_{2}$. By choosing different position parameters b1 and b2, we have shown three types of bounded states with different interaction forces. In the future, we will continue to analyze the IST and solutions for the MTM system with nonzero boundary conditions.