1. Introduction
Entanglement [1–3] serves as a crucial quantum resource, simplifying and, in many cases, enabling the execution of various quantum information tasks. Its applications span across quantum computing [4, 5], quantum communications [6, 7], quantum cryptography [8], and the security of devices with quantum capabilities [9, 10].
Significant progress has been achieved in understanding this purely quantum feature [11]. However, despite these advances, a satisfactory description exists only for bipartite entanglement in two-dimensional systems, specifically qubits. When extending to higher-dimensional subsystems or increasing the number of qubits in the overall system, a proper description remains elusive.
In the case of multipartite systems, the classification of entangled states becomes more intricate compared to bipartite systems. Rather than a simple categorization of separable or entangled for bipartite states, one must specify whether multipartite states are partially entangled or fully entangled. Moreover, the number of combinations of different components increases exponentially, resulting in a multitude of ways to share entanglement among the components, each defining a distinct class of multipartite entanglement [12, 13]. However, this is not the sole method of defining such classes, as various classifications exist based on alternative properties of multipartite entanglements.
The fundamental concept involves categorizing quantum states into distinct families, comprising sets of states that may exhibit shared symmetries or specific structural characteristics. Alternatively, if these quantum states can be generated using a particular procedure, the potential exists for mapping a designated set of states onto another collection precisely described through a specific parametric representation. For instance, classification methods based on local operations and classical communications (LOCC) [12] extend the idea of stochastic LOCC (SLOCC) [14], or classifications based on persistent homology [15].
Achieving a well-defined classification of multipartite entanglement is crucial, given that quantum information processing tasks based on multipartite entanglement are highly sensitive to the specific class of entanglement being utilized [8, 10, 16, 17]. Each quantum task demands a particular feature from the multipartite entanglement on which it relies, especially concerning its behavior when one or more components are traced out. Therefore, a prerequisite for asserting the relevance of a given state to a quantum task is knowing the class to which it belongs.
In recent years, the intersection of quantum information processing [4] and machine learning [18, 19] has led to the emergence of a new discipline: quantum machine learning [20–23]. This integration can occur in four ways. Quantum versions of machine learning algorithms can be developed for performing classical or quantum tasks [24]. Alternatively, classical machine learning algorithms have been shown to be effective in solving quantum tasks, particularly in classification [25, 26], where classical algorithms manipulate quantum data. We adopt this approach in our study, evaluating the performance of classical machine learning algorithms in the general classification of full multipartite entanglement for both pure and mixed states, avoiding complex computations involving numerous parameters for state classification.
To achieve this, we start with the presentation of our classification of fully entangled states in section 2 . We demonstrate how this classification, rooted in the use of tangle as a measure or detection of multipartite entanglement, naturally emerges. The resulting classification tree and its implications for two, three, and four qubits are discussed. Section 3 outlines the strategy employed for implementing the classification of fully entangled multipartite states using deep learning artificial neural networks. We introduce the data set used for the learning and testing phases of the protocol. The section concludes with the presentation of the results, including the confusion matrix and a table of verification. The article concludes with a discussion and perspectives on the current work. An appendix is included, containing the definitions of the entanglement measures applied to pure states.
2. Classification of fully entangled states
An arbitrary quantum system A1 ⨂...⨂ AN, with N subsystems, described by the density matrix $\rho \in { \mathcal H }\,={{ \mathcal H }}^{{A}_{1}}\otimes ...\otimes {{ \mathcal H }}^{{A}_{N}}$ is called fully-separable if and only if ρ can be written in the form $\rho ={\rho }_{{A}_{1}}\otimes ...\otimes {\rho }_{{A}_{N}}$, where ${\rho }_{{A}_{i}}$ are reduced density matrices of the individual subsystems from ${{ \mathcal H }}^{{A}_{i}}$. Conversely, if ρ can be represented as a tensor product of k sub-states: ρ = ρ1 ⨂...⨂ ρk with k < N then it is called k-separable i.e. some subsystems are separable from the rest which is entangled [27]. Beyond these scenarios, when ρ does not fall into either the fully separable or k-separable categories, it is labeled as fully entangled or 'non-k-separable' [28]. In such cases, all parties of the system are entangled.
In this paper, we focus our attention on fully entangled multipartite systems, as the discussion of k-separable states classification is always amenable to that of fully entangled ones in a lower dimensional Hilbert space.
2.1. Entanglement quantifiers and detectors
Concurrence is a well-established measure of entanglement in the case of two qubits systems [29]. But when we are dealing with more than two qubits (multipartite systems), things get more complex. There are different ways to adapt the idea of concurrence to evaluate the entanglement between different subsystems.
One way is to add up the concurrence values for all possible pairs of qubits we call this the cumulative concurrence [30]. Another method involves multiplying the concurrence values between these pairs; this is known as the product of concurrences [31]. The choice between these methods depends on the specifics of the problem we are dealing with.
In our work, we employ both the product and summation principles within the lower bounds framework [32]. The choice between these methods is influenced by the type of entanglement we are investigating and how the qubits are grouped together. We opt for these approaches because the lower bound we utilize establishes a starting point of zero for a completely separable multipartite state. Thus, if the value surpasses zero, it signals the presence of some form of entanglement in the quantum state we are examining.
Moving forward, we provide detailed definitions of the lower bound of concurrence designed specifically for our study, accommodating both pure and mixed states. We introduce τ1 as an indicator of fully entangled states, relying on the product over all possible bipartitions p:
$\begin{eqnarray}{\tau }_{1}={\left(\displaystyle \prod _{p}\displaystyle \sum _{\alpha \beta }{({C}_{\alpha ,\beta }^{p})}^{2}\right)}^{\frac{1}{m}}.\end{eqnarray}$
As a matter of fact, τ1 is zero when at least one subsystem is separable from the others.Moreover, for an N-qubit system, we define τi, where 2 ≤ i ≤ N, as the average i-tuple entanglement. For example, τ2 characterizes the average entanglement across all 2-qubit subsystems and is determined as follows:
$\begin{eqnarray}{\tau }_{2}=\frac{1}{\left(\genfrac{}{}{0.0pt}{}{N}{2}\right)}\left(\displaystyle \sum _{i,j}{({C}_{ij})}^{2}\right).\end{eqnarray}$
Similarly for higher values of subscript i : $\begin{eqnarray}\begin{array}{rcl}{\tau }_{3} & = & \frac{1}{\left(\genfrac{}{}{0.0pt}{}{N}{3}\right)}\left(\displaystyle \sum _{i,j,k}(\frac{1}{3}\displaystyle \sum _{\alpha ,\beta }[\,{({C}_{\alpha \beta }^{ij/k})}^{2}\right.\\ & & \left.+{({C}_{\alpha \beta }^{i/kj})}^{2}+{({C}_{\alpha \beta }^{jk/i})}^{2}])\Space{0ex}{3.45ex}{0ex}\right),\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl}{\tau }_{4} & = & \frac{1}{\left(\genfrac{}{}{0.0pt}{}{N}{4}\right)}\left(\displaystyle \sum _{i,j,k,l}(\frac{1}{7}\displaystyle \sum _{\alpha ,\beta }[\,{({C}_{\alpha \beta }^{i/jkl})}^{2}+{({C}_{\alpha \beta }^{j/ikl})}^{2}\right.\\ & & +{({C}_{\alpha \beta }^{k/jil})}^{2}+{({C}_{\alpha \beta }^{ijk/l})}^{2}+{({C}_{\alpha \beta }^{ij/kl})}^{2}\\ & & \left.+{({C}_{\alpha \beta }^{ik/jl})}^{2}+{({C}_{\alpha \beta }^{il/kj})}^{2}])\Space{0ex}{3.45ex}{0ex}\right),\end{array}\end{eqnarray}$
$\begin{eqnarray}\begin{array}{rcl} & \vdots & \\ {\tau }_{N} & = & \frac{1}{\left(\genfrac{}{}{0.0pt}{}{N}{N}\right)}\left(\frac{1}{m}\displaystyle \sum _{p}\displaystyle \sum _{\alpha ,\beta }[\,{({C}_{\alpha \beta }^{p})}^{2}]\right).\,\end{array}\end{eqnarray}$
In the above definitions, m = 2N−1 − 1, N being the number of qubits and $\left(\genfrac{}{}{0.0pt}{}{N}{i}\right)$ the binomial coefficient, giving all possible i-tuples out of N qubits. ${C}_{\alpha \beta }^{p}$ represents the entanglement shared in a bipartition p, with an arbitrary dimension for each subsystem. It is given by the lower bound of concurrence [32] defined by:
$\begin{eqnarray}\begin{array}{rcl}{C}_{\alpha \beta }^{p} & = & \,\rm{max}\,\{0,\lambda {(1)}_{\alpha \beta }^{p}-\lambda {(2)}_{\alpha \beta }^{p}-\lambda {(3)}_{\alpha \beta }^{p}\\ & & -\lambda {(4)}_{\alpha \beta }^{p}\},\end{array}\end{eqnarray}$
where $\lambda {(i)}_{\alpha \beta }^{p}$ are the square roots of the four non-zero eigenvalues, in decreasing order, of the non-Hermitian matrix $\sqrt{\rho {\tilde{\rho }}_{\alpha \beta }}$, with ${\tilde{\rho }}_{\alpha \beta }=({L}_{\alpha }\otimes {L}_{\beta }){\rho }^{* }({L}_{\alpha }\otimes {L}_{\beta })$, and Lα and Lβ being generators of SO(d).In the case of two qubits, ${C}_{\alpha \beta }^{p}$ reduces to Ci/j used in equation (2 ) which is the Wooter's concurrence [29] representing 2-qubit entanglement. It is defined by:
$\begin{eqnarray}{C}_{i/j}=\,\rm{max}\,\{0,\lambda (1)-\lambda (2)-\lambda (3)-\lambda (4)\},\end{eqnarray}$
where the λ(i) are the eigenvalues, in decreasing order, of the Hermitian matrix $\sqrt{\sqrt{\rho }\tilde{\rho }\sqrt{\rho }}$, with $\tilde{\rho }=({\sigma }_{y}\otimes {\sigma }_{y}){\rho }^{* }({\sigma }_{y}\otimes {\sigma }_{y})$.The choice of the product ∏p in equation (1 ) is based on its suitability for determining whether a given state is fully entangled or not using τ1. This product is applied over all possible combinations, allowing us to assess full entanglement.
For τN, the sum ∑p is calculated across all possible partitions p, ensuring that for fully separable multipartite states, τN = 0. This definition ensures that τN > 0 indicates the presence of at least some level of entanglement within the quantum state. Consequently, if a state is fully entangled and contains entanglement not detected in its subsystems, it qualifies as genuine N-entanglement.
It is worth noting that in the case of pure states (specifically, three and four qubits), it is more appropriate to use the pure-states-tangleτ3 (12 ) and τ4 (14 ), respectively quantifying 3-way and 4-way entanglement. This is due to their enhanced ability to precisely quantify genuine N-entanglement rather than just detecting it.
Importantly, a fully entangled state can encompass one or more types of entanglement, considering the monogamous property [33, 34] or the symmetries of the systems. These factors dictate the necessity of establishing a precedence order in this classification, a point that will be further explored in the following section.
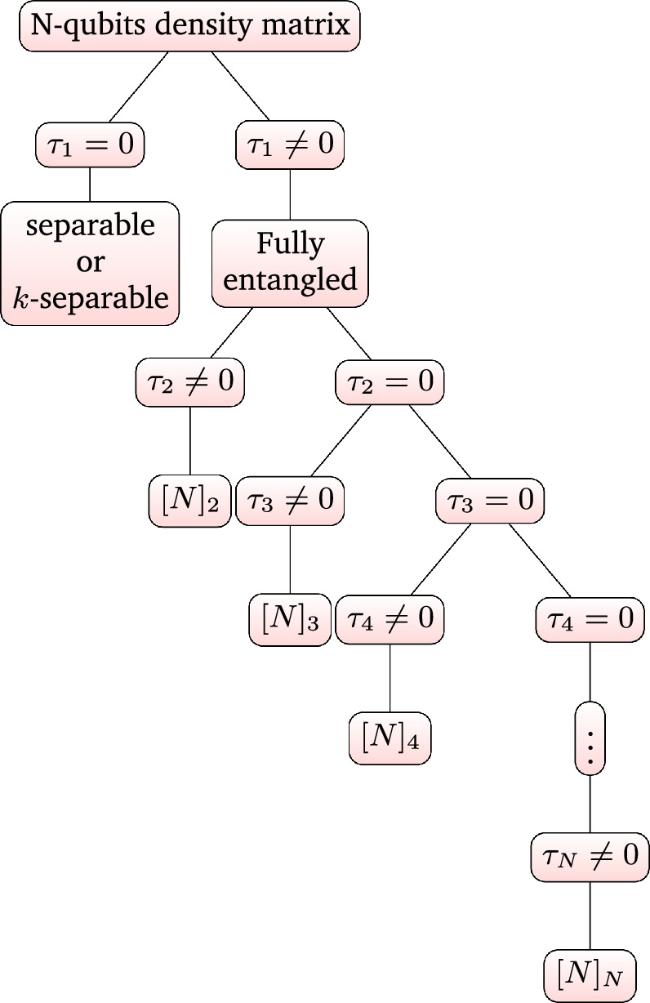
2.2. Classification tree
The initial classification of an arbitrary N-qubit state, falls into one of three categories: fully separable, k-separable, or fully entangled. If it is fully entangled, the next step is to identify the specific type of entanglement present. This is done by sequentially checking for the existence of 2-entanglement (qubit-qubit entanglement), 3-entanglement, and so forth, up to the point where only states containing the genuine N-entanglement are present. These categories are denoted as [N]2, [N]3, and finally [N]N, representing fully entangled states.
The [N]N class, signifying states with genuine N-entanglement, is expected to be the most susceptible to changes under partial trace operations. This fragility emphasizes the intricate nature of the highest level of entanglement in the quantum state, making it a crucial consideration in the overall classification scheme.
This process is illustrated through a hierarchical tree, that is depicted in figure 1.
Figure 1. Classification of entanglement for N-qubit states. |
2.3. Types of entanglement in symmetric systems
In the context of symmetric systems, our classification system gauges the 'fragility' of entanglement in a given state when subjected to a partial trace operation [35] over its subsystems. The detection of each type of entanglement relies on the use of the i-tangles defined in subsection 2.1 .
Consider a symmetrical state $\rho \in { \mathcal H }=\mathop{\underbrace{{{ \mathcal H }}^{2}\otimes \ldots \otimes {{ \mathcal H }}^{2}}}\limits_{\times N}$ of N parties. In this case, ρ can exhibit full entanglement in N − 1 distinct ways.
N-entanglement, where performing a partial trace over any individual subsystem yields a separable state. This type of entanglement is genuinely shared among all N parties.
(N − 1)-entanglement, which disappears when tracing out any two individual subsystems. This entanglement is shared among (N − 1)-tuples.
$\begin{eqnarray*}\vdots \end{eqnarray*}$
The 2-entanglement, being the most resilient against partial trace operations, as persists even when traced out over any (N − 2) subsystems. Here, entanglement is shared among all possible pairs.
More generally, the (N − i)-entanglement vanishes upon tracing over any (i + 1) qubits, and this entanglement is distributed among (N − i)-tuples. Therefore, quantifying this entanglement is accomplished using the (N − i)-tangle (τN−i), as defined in section 2.1 .
The core of this concept lies in establishing a systematic classification methodology based on the behavior of entangled states under partial trace operations. Leveraging the fragility of entangled states, this approach aims to categorize and understand their intricacies. By closely examining how these states respond to partial trace operations-operations designed to selectively capture the behavior of specific subsets of components-this classification framework reveals profound insights into the underlying structures of entanglement.
This framework not only provides a fresh perspective on understanding entanglement but also holds potential for significant impacts across diverse fields, including quantum computing, communication, and cryptography. It stands poised to offer deep insights into the resilience or vulnerability of entanglement under various scenarios. The differentiation among different entanglement classes depends on their respective capacities to endure successive applications of partial trace operations. Figure 2 provides a schematic representation of this procedure in the context of four qubits, visually illustrating the essence of the classification process
Figure 2. The fragility of the entanglement in each class over the partial trace. |
The outcomes of the classification reveal intriguing patterns. As illustrated in figure 3, a set of symmetrically fully entangled four qubits unveils three distinct classes of entanglement: [4]4, [4]3, and [4]2. These classes denote different configurations of entanglement within the four-qubit system. Similarly, for three qubits, the classification identifies two classes: [3]3 and [3]2. Finally, in the case of a pair of qubits, the classification recognizes a single class denoted as [2]2, representing a unique form of entanglement between two qubits. The intriguing aspect lies in how the distribution of entanglement across these qubit partitions shapes the resulting classes. Essentially, this classification framework provides a systematic approach to understanding and describing the entanglement relationships that emerge among qubits in various arrangements. Such insights are invaluable for advancing our comprehension of quantum phenomena and applying them in quantum computing and other quantum technologies.
Figure 3. Entanglement classes in symmetric fully entangled states for four, three, and two qubits partitions. |
3. Classification using machine learning
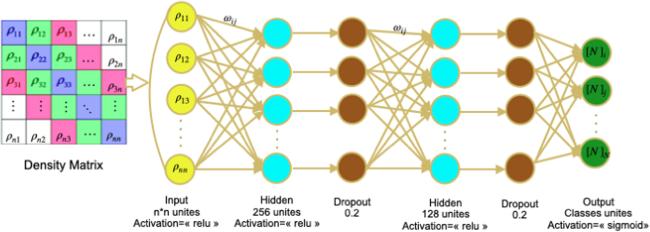
3.1. Machine learning, deep learning and artificial neural networks
Machine learning, as defined by Mitchell [18], is an application of artificial intelligence (AI) that enables systems to autonomously learn tasks without explicit programming. It involves developing algorithms capable of accessing data to learn independently, without requiring intervention from a programmer. The three primary types of machine learning methods are supervised, unsupervised, and reinforcement learning.
In our current study, we employ supervised learning methods, where the class (output) of each state (input) in a sample is known. The objective is to discover a function that optimally maps inputs to outputs and utilizes it for classifying new states.
Deep Learning, a subset of machine learning explored by researchers such as LeCun et al [36], is dedicated to algorithms inspired by the structure and function of the human brain, known as Artificial Neural Networks (ANN). In this context, each 'Neuron', referred to as a perceptron in Artificial Intelligence (AI), operates as a mathematical function that organizes and categorizes information based on a specific structure.
In multi-layer perceptrons (MLP), these perceptrons are organized in interconnected layers. An input layer (sensory unit) collects input patterns, an output layer (response unit) contains classifications or exit values, and hidden layers (associator unit) adjust input weights to minimize neural network loss. It is assumed that these hidden layers capture the essential features of the input data, contributing to predictive power regarding the corresponding output. In our application, these features are the density matrix elements or their combinations responsible for each entanglement class.
Our neural network architecture, outlined in figure 4, is crafted using the Keras library [37]. This sequential model comprises four densely connected layers interleaved with two dropout layers to mitigate overfitting. The pattern alternates between dense layers, capturing patterns in density matrix elements, and dropout layers that deactivate a random subset of neurons to prevent over-reliance on specific ones. The first dense layer, with 16, 64, or 256 neurons depending on the number of qubits (two, three, or four respectively), is followed by a second dense layer of 256 neurons using the ReLU activation function [38], along with a dropout layer. The third dense layer features 128 neurons with ReLU activation, followed by a final dropout layer. The output layer, designed for a classification task, employs sigmoid activation [39] and matches the number of classes for each case. The chosen loss function, Sparse Categorical Cross-Entropy, is defined as:
$\begin{eqnarray}\,\rm{Loss}\,=-\frac{1}{N}\displaystyle \sum _{i=1}^{N}{y}_{i}\mathrm{log}({\hat{y}}_{i}),\end{eqnarray}$
where yi is the true label, and ${\hat{y}}_{i}$ is the predicted label. Sparse Categorical Cross-Entropy is well-suited for multi-class classification scenarios where the true class labels are provided as integer indices rather than one-hot encoded vectors. This loss function effectively computes the difference between the predicted probabilities and the integer class labels, allowing for efficient training, especially when dealing with a large number of classes. In contrast, the commonly used cross-entropy loss function (or categorical cross-entropy) requires the target labels to be one-hot encoded, where each class is represented as a binary vector. This representation can lead to increased memory consumption and computational overhead, particularly in multi-class problems with many classes. By utilizing Sparse Categorical Cross-Entropy, our architecture streamlines the learning process and reduces resource requirements. Our model is optimized using the Adam optimizer [40], which enhances convergence speed and accuracy in the classification task through iterative learning.
Figure 4. The adopted architecture of the Neural Network. |
3.2. Data set
The approach for preparing the data set is contingent upon the system's dimension. Here, we delineate the procedure based on the total number of qubits under consideration. To generate random density matrices, we employ the algorithm proposed by Zyczkowski et al [41]. This algorithm is rooted in the concept that any density matrix can be expressed as a convex combination of pure states, denoted as ρ = ∑ipi∣ψi⟩⟨ψi∣, where pi represents probabilities and ∣ψi⟩ are random pure states. We implement this algorithm using the QuTip Python package, applying the standard rand_dm function.
Bipartite states:
1. Generate a random density matrix state ρ of 2 qubits.
2. Compute the concurrence of ρ. If it is equal to 0 we save ρ in our data set as 'Separable', else we save it as 'Entangled'.
Multipartite states:
1. Generate a random density matrix state ρ according to the number of qubits In our application we use 3-qubits and 4-qubits systems.
2. Compute the different i-tangles and assign the corresponding class according to the classification established in section
For 3 qubits, if τ1 = 0, we save ρ in our data set as 'separable', else if τ2 ≠ 0, we save it in our data set as '[3]2', else we save it as '[3]3'.
For 4 qubits, if τ1 = 0, we save ρ in our data set as 'separable', else if τ2 ≠ 0, we save it in our data set as '[4]2', else if τ3 ≠ 0 we save it as '[4]3', else we save it as '[4]4'.
The final data set we generated consists of 540 000 density matrices scattered as follows:
for 2-qubit systems, we generated 400 000 density matrices, 200 000 pure and 200 000 mixed, each type containing 100 000 of each class separable/entangled.
for 3-qubit systems, we generated 60 000 density matrices, 30 000 pure and 30 000 mixed, each type containing 10 000 of each class k-separable or separable /[3]2/[3]3.
for 4-qubit systems, we generated 80 000 density matrices, 40 000 pure and 40 000 mixed, each type containing 10 000 of each class k-separable or separable /[4]2/[4]3/[4]4.
The discrepancy in the number of data generated is mainly due to the increase in the number of elements to be generated accompanying the increase in the number of q-bits. For instance, for a system of 2-qubits only 22 × 22 = 16 elements are needed while for 4-qubits, one needs 24 × 24 = 256 elements, all while imposing the density matrices conditions. It turns out that some classes are easier (quicker) to generate than others, however, to equilibrate things we chose equal numbers of each class generated.
This data was generated through computational resources of HPC-MARWAN (hpc.marwan.ma) provided by the National Center for Scientific and Technical Research (CNRST), Rabat, Morocco.
3.3. Results
After data preparation, the initial task involves training the ANN classifiers to differentiate between various classes. To comprehensively evaluate the classifier's performance, we eliminate redundancy, ensuring that the training and testing datasets are entirely distinct. The data set is split into two parts: 80% for training and 20% for testing. This division is crucial for assessing the model's robustness against overfitting and other potential issues. A model is considered effective if it demonstrates high performance during the testing phase, indicating its ability to generalize to new information.
To illustrate the performance of our classifiers, we utilize error matrices, commonly known as confusion matrices [42]. These matrices are two-dimensional tables, or (N, N) matrices, where N represents the number of classes. One dimension corresponds to the true class, while the other represents the predicted class. The diagonal elements of these matrices indicate the number of samples correctly classified (successful predictions), while the off-diagonal elements signify the number of samples for which the predicted class is incorrect.
Various metrics, derived from the confusion matrix, facilitate the assessment of classification performance. In the following analysis, we employ the Accuracy and Precisioni for a specific class i, as defined subsequently.
1. Accuracy, is the proportion of the total number of correct predictions:
$\begin{eqnarray}\,\rm{Accuracy}\,=\frac{\displaystyle {\sum }_{i-1}^{N}{M}_{ii}}{\displaystyle {\sum }_{i-1}^{N}\displaystyle {\sum }_{j=1}^{N}{M}_{ij}}.\end{eqnarray}$
2. Precision, is a measure of the number of cases in which a specific class i has been correctly predicted:
$\begin{eqnarray}{\,\rm{Precision}\,}_{i}=\frac{{M}_{ii}}{\displaystyle {\sum }_{k=1}^{N}{M}_{ki}}.\end{eqnarray}$
In the above definitions, Mij are the confusion matrix elements and N is the number of classes.Figures 5, 6, and 7 illustrate the testing confusion matrices for bipartite, tripartite, and four-partite states, respectively. In each matrix, the rows represent the true classes, while the columns correspond to the predicted classes. The entries of the matrix provide the number of states and their proportions.
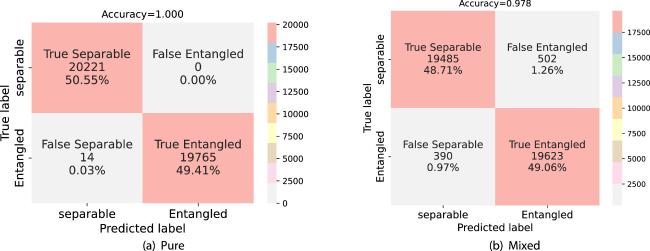
Figure 5. The testing confusion matrix for the classification of pure (a) and mixed (b) bipartite density matrices. |
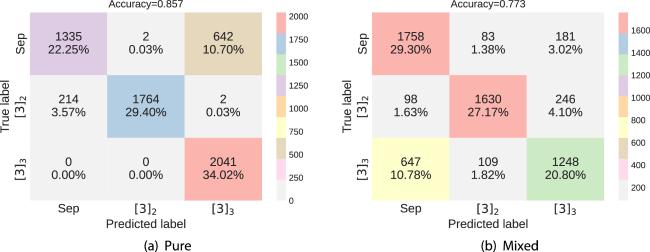
Figure 6. The testing confusion matrix for the classification of pure (a) and mixed (b) tripartite density matrices. |
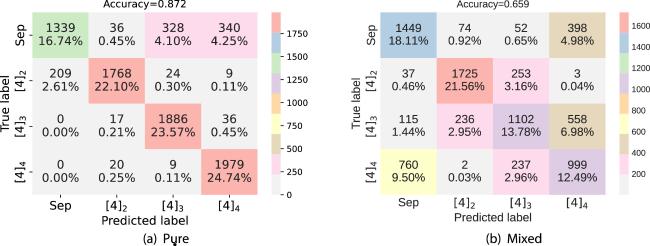
Figure 7. The testing confusion matrix for the classification of pure (a) and mixed (b) four-partite density matrices. |
For bipartite states, our classifier achieved an almost perfect overall performance, with 99.6% accuracy for pure states and 97.8% for mixed states. The precision for correctly classifying entangled states was 99.92% for pure states and 98.05% for mixed states, while separable states were classified with 100% precision for pure states and 97.48% for mixed states.
Moving to tripartite states, the overall performance was 85.7% for pure systems and 77.3% for mixed systems. The classifier accurately classified separable/k-separable states with 86.18% precision for pure states and 86.94% for mixed states. Additionally, [3]2 states were classified with 89.09% precision for pure states and 82.57% for mixed states, while [3]3 states were classified with 100% precision for pure states and 62.27% for mixed states.
For four-partite states, the overall performance was 87.2% for pure states and 65.9% for mixed states. Separable/k-separable states were accurately classified with 86.49% precision for pure states and 73.44% for mixed states. Furthermore, [4]2 states were classified with 96.03% precision for pure systems and 85.48% for mixed systems; [4]3 states with 83.93% precision for pure systems and 54.79% for mixed states, and [4]4 states with 83.71% precision for pure states and 50% for mixed states.
To evaluate the significance of employing Machine Learning in the quantum information domain, we conducted tests using our classifier on well-known separable/k-separable states and representative states from various classes. The tested states include the four Bell states for 2-qubits, ∣GHZ3⟩ and ∣W3⟩ states for 3-qubits, and ∣GHZ4⟩, ∣W4⟩ for 4-qubits. Additionally, mixtures of these representative states were included in the test to assess the classifier's performance with mixed states. The results of this test are summarized in table 1.
Table 1. Verification of the classification of some well-known pure states. |
| Verification of pure states | |||
|---|---|---|---|
| Dim | State | True class | Predict class |
| 2 qubits | $| {\psi }_{1}\rangle =\frac{1}{\sqrt{2}}(| 00\rangle +| 11\rangle )$ | Ent | Ent ✓ |
| $| {\psi }_{2}\rangle =\frac{1}{\sqrt{2}}(| 01\rangle +| 10\rangle )$ | Ent | Ent ✓ | |
| $| {\psi }_{3}\rangle =\frac{1}{\sqrt{2}}(| 00\rangle -| 11\rangle )$ | Ent | Ent ✓ | |
| $| {\psi }_{4}\rangle =\frac{1}{\sqrt{2}}(| 01\rangle -| 10\rangle )$ | Ent | Ent ✓ | |
| $| {\psi }_{5}\rangle =\frac{1}{\sqrt{2}}(| 00\rangle +| 01\rangle )$ | Sep | Sep ✓ | |
| $| {\psi }_{6}\rangle =\frac{1}{\sqrt{2}}(| 10\rangle +| 11\rangle )$ | Sep | sep ✓ | |
| $| {\psi }_{7}\rangle =\frac{1}{2}(| 00\rangle +| 01\rangle +| 10\rangle +| 11\rangle )$ | Sep | Sep ✓ | |
| | |||
| 3 qubits | $| {\phi }_{1}\rangle =\frac{1}{\sqrt{2}}(| 000\rangle +| 111\rangle )$ | [3]3 | [3]3✓ |
| $| {\phi }_{2}\rangle =\frac{1}{\sqrt{3}}(| 001\rangle +| 010\rangle +| 100\rangle )$ | [3]2 | [3]2✓ | |
| $| {\phi }_{3}\rangle =\frac{1}{\sqrt{3}}(| 110\rangle +| 101\rangle +| 011\rangle )$ | [3]2 | [3]2✓ | |
| $| {\phi }_{4}\rangle =\frac{1}{\sqrt{3}}(| 010\rangle +| 001\rangle +| 011\rangle )$ | K-Sep | Sep ✓ | |
| $| {\phi }_{5}\rangle =\frac{1}{\sqrt{2}}(| 000\rangle +| 001\rangle )$ | Sep | [3]3 ✗ | |
| | |||
| 4 qubits | $| {\chi }_{1}\rangle =\frac{1}{\sqrt{2}}(| 0000\rangle +| 1111\rangle )$ | [4]4 | [4]4✓ |
| $| {\chi }_{2}\rangle =\frac{1}{2}(| 0001\rangle +| 0010\rangle +| 0100\rangle +| 1000\rangle )$ | [4]2 | [4]2✓ | |
| $| {\chi }_{3}\rangle =\frac{1}{2}(| 1110\rangle +| 1101\rangle +| 1011\rangle +| 0111\rangle )$ | [4]2 | Sep ✗ | |
| $| {\chi }_{4}\rangle =\frac{1}{\sqrt{5}}(| 0000\rangle +| 0111\rangle +| 1011\rangle +| 1101\rangle +| 1110\rangle )$ | [4]3 | [4]3✓ | |
| $| {\chi }_{5}\rangle =\frac{1}{\sqrt{5}}(| 1000\rangle +| 0100\rangle +| 0010\rangle +| 0001\rangle +| 1111\rangle )$ | [4]3 | [4]3✓ | |
| $| {\chi }_{6}\rangle =\frac{1}{2}(| 0000\rangle +| 0011\rangle +| 0010\rangle +| 0001\rangle )$ | K-Sep | Sep ✓ | |
Furthermore, it is important to note that due to the randomness of the generated density matrices, the results obtained from this classifier extend beyond the specific set of tested states. The classifier's applicability is not limited to the explicitly tested states, making it a versatile tool for classifying entanglement in density matrices for 2, 3, or 4 qubits. The robustness of the classifier enables its use in a broad range of quantum states, providing valuable insights into the entanglement properties of diverse quantum systems.
If the classifier performs well on a diverse set of states, including mixtures and representative states, it suggests a robust ability to predict the entanglement behavior in similar systems. This implies that the classifier can generalize its understanding and predictions to density matrices that describe the same systems or are more similar in nature.
Tables 1 and 2 affirm the performance of our model in accurately distinguishing between different classes of well-known quantum states. Notably, errors documented in the tables originate from elements of the confusion matrix with elevated error percentages, aligning with observations from the confusion matrices (figures 5, 6, and 7).
Table 2. Verification of the classification of some mixture of the states used in table 1. |
| Verification of mixed states | |||
|---|---|---|---|
| Dim | State | True class | Predict class |
| 2 qubits | ρ1 = 0.5(∣ψ1⟩⟨ψ1∣) + 0.5(∣ψ3⟩⟨ψ3∣) | Sep | Sep ✓ |
| ρ2 = 0.8(∣ψ1⟩⟨ψ1∣) + 0.2(∣ψ3⟩⟨ψ3∣) | Ent | Ent ✓ | |
| ρ3 = 0.5(∣ψ2⟩⟨ψ2∣) + 0.5(∣ψ6⟩⟨ψ6∣) | Sep | Sep ✓ | |
| ρ4 = 0.8(∣ψ2⟩⟨ψ2∣) + 0.2(∣ψ6⟩⟨ψ6∣) | Ent | Ent ✓ | |
| | |||
| 3 qubits | σ1 = 0.8(∣φ1⟩⟨φ1∣) + 0.2(∣φ3⟩⟨φ3∣) | [3]3 | [3]3✓ |
| σ2 = 0.8(∣φ1⟩⟨φ1∣) + 0.2(∣φ3⟩⟨φ3∣) | [3]3 | [3]3✓ | |
| σ3 = 0.8(∣φ1⟩⟨φ1∣) + 0.2(∣φ3⟩⟨φ3∣) | [3]3 | [3]3✓ | |
| σ4 = 0.8(∣φ1⟩⟨φ1∣) + 0.2(∣φ3⟩⟨φ3∣) | [3]3 | Sep ✗ | |
| | |||
| 4 qubits | μ1 = 0.5(∣χ1⟩⟨χ1∣) + 0.5(∣χ3⟩⟨χ3∣) | [4]4 | [4]4✓ |
| μ2 = 0.2(∣χ2⟩⟨χ2∣) + 0.8(∣χ4⟩⟨χ4∣) | [4]3 | [4]3✓ | |
| μ3 = 0.8(∣χ6⟩⟨χ6∣) + 0.2(∣χ5⟩⟨χ5∣) | Sep | Sep ✓ | |
| μ4 = 0.8(∣χ1⟩⟨χ1∣) + 0.2(∣χ3⟩⟨χ3∣) | [4]4 | Sep ✗ | |
| μ5 = 0.8(∣χ5⟩⟨χ5∣) + 0.2(∣χ2⟩⟨χ2∣) | [4]3 | [4]4 ✗ | |
A noteworthy observation from tables 1 and 2 is that the majority of errors occur in cases where the number and spatial distribution of non-zero density matrix elements in the tested state closely resemble those of well-established states, such as the representative states (e.g. ∣φ5⟩, which bears resemblance to ∣φ1⟩ in terms of state shape). Remarkably, these errors persist even when the states belong to different entanglement classes. This underscores the model's sensitivity to subtle differences in quantum states, especially when their characteristics closely resemble those of other classes. Importantly, it highlights the classifier's ability to extract entanglement information from the density matrix elements, contributing to its discerning capabilities in classifying quantum states.
4. Discussion and conclusion
In summary, we have introduced a new classification for multipartite fully entangled states based on the distribution of entanglement between the subsystems. We have used a neural networks model to automatically classify random quantum states, without the need to explicitly calculate the corresponding entanglement measures each time. Instead, the NN model learns to distinguish the different classes directly from the density matrix elements.
In the application we classified states of two, three, and four qubits, into separable (or k-separable) and fully entangled states while specifying the corresponding class denoted [N]j, where the index j = 2, …, N, specifies the actual class given the number of qubits N.
The proposed algorithm can be integrated into any quantum information processing protocol that relies on a specific type of entanglement or, for that matter, adapts depending on the class of multipartite entanglement detected. As a matter of fact, The importance of any classification scheme stems from the usefulness of the resulting types of multipartite entanglement in the targeted applications.
As an illustration for this, let us consider a given teleportation protocol involving three parties (Alice and Bob being the primary parties and Charlie being an ancilla) that share an entangled state. When Alice teleports an arbitrary qubit to Bob, if she decides to break the operation in the case Charlie measures his qubit, then they need to use a [3]3 class state. Otherwise, if Alice wants to continue this teleportation independently of Charlie's qubit, they'll need to use a [3]2 class state. Following alternative lines of thought, a quantum teleportation protocol was introduced in [43] and a comparison of the efficiency of different 4-qubit states to teleport two qubits resulted in the GHZ state (belonging to the [4]4 class) being more efficient than the W state which belongs to the [4]2 class. Notwithstanding the foregoing, [44] establishes that a 4-qubit GHZ state class is not a good candidate for perfect quantum teleportation using their protocol and the so-called χ state [16], which falls in the class [4]3 of our classification, provides a better channel.
As another field of application, quantum radars [10] make use of fully entangled particles, whereby one part is kept in the system while the other parties are sent toward a target. So when one of the sent particles is traced out (interacting with the environment), the loss of entanglement with the other particles depends on the class of entangled state chosen in the first place. Bearing this in mind, it is evident that while states with genuine multipartite entanglement (N-entanglement) will have higher efficiency, they will be more vulnerable to the interaction with environment. So in this case an optimization procedure is necessary depending on the types of interactions in play.
Other results suggest that multipartite entanglement speeds up quantum key distribution in networks [8], reaching different performances with different classes of entanglement.
The results of this paper can be exploited in other directions as well. Among these, work is in progress to implement this technique to detect the entanglement transitions from one class to another in dynamical systems. It will be interesting to investigate the generalization to larger dimensions and deal with qudits instead of qubits. This is even so important as the existence of a proper measure of entanglement even in the bipartite case is still debated.
As a final note, it is believed that using quantum machine learning algorithms will be more efficient, especially in cases where the accuracy of the current technique is relatively small (like in the case of four-partite mixed states here). This belief comes from the fact, that quantum algorithms should recognize quantum features (like entanglement) more 'intuitively', thus resulting in more accurate classification schemes [21].