1. Introduction
On August 17th 2017, the first observation of gravitational waves (GW) from a binary neutron star (BNS) merger [1], together with the first joint observation of GW from a BNS merger and its electromagnetic (EM) counterpart [2, 3], marked the beginning of a new era in multi-messenger astronomy and cosmology. The measurement of the GW signal directly provides information on the absolute luminosity distance to the source, while its redshift can be determined by identifying the EM counterpart of the GW source. This establishes an absolute distance-redshift relation, known as the standard siren method, which is crucial for cosmological studies. To date, only one bright siren, GW170817, has been identified. This is insufficient to probe cosmological parameters using current standard sirens, necessitating the use of next-generation GW detectors.
In the future, third-generation (3G) ground-based GW detectors, such as the Einstein Telescope (ET) [4, 5] in Europe and the Cosmic Explorer (CE) [6, 7] in the United States will become operational, with sensitivities improved one order of magnitude over the current detectors, and much more BNS merger events will be observed at much deeper redshifts. Recently, GW standard sirens have been widely discussed in the literature [8–47]. It has been found that future observations of GW standard sirens from the ET and CE will play a crucial role in the estimation of cosmological parameters [14, 16, 22, 25, 26, 28, 37, 38, 43, 46]. In particular, the GW standard sirens can break the parameter degeneracies generated by the current EM cosmological observations, thereby improving constraints on neutrino mass, see [14, 37].
A recent forecast [46] demonstrated that joint observations of BNS by 3G GW detectors and short γ-ray burst (GRB) observations by missions similar to the THESEUS satellite project can improve the constraints on the total active neutrino mass. Therefore, it is crucial to investigate how the combined GW-GRB observations would affect constraints on the sterile neutrino parameters.
The existence of light sterile neutrinos has been suggested by anomalies in short-baseline (SBL) neutrino experiments [48–57]. To explain the SBL neutrino oscillation data, sterile neutrinos with eV-scale masses are required [58–60]. Cosmological observations play a crucial role in constraining the mass of active neutrinos (see [61–108]). Since sterile neutrinos have implications for the evolution of the Universe, cosmology can provide an independent test for their existence. For related works on sterile neutrinos, see [109–134].
Currently, one of the most significant challenges in cosmology is the 'Hubble tension' [135], which refers to the discrepancy between early and late Universe observations. In the past few years, people often considered models that include light sterile neutrinos to alleviate the Hubble constant crisis. This is because when using the cosmic microwave background data to constrain cosmological parameters, the effective number of neutrino species (Neff) is positively correlated with the Hubble constant; if Neff is larger, the derived Hubble constant will also be larger. See [118, 125–128, 130, 131, 134], for related studies. However, in recent years, the results of cosmological observation fits have shown that the effect of using this method to alleviate the Hubble crisis is no longer significant. Nevertheless, due to the significant correlation between Neff and H0, precise measurements of the Hubble constant using gravitational wave standard sirens are very helpful for determining the parameters of sterile neutrinos.
Additionally, the main advantage of the standard siren method for measuring the Hubble constant is that it avoids relying on the cosmic distance ladder. Therefore, in the future, the GW standard sirens could become a promising cosmological probe, playing a crucial role in measuring cosmological parameters, including those related to sterile neutrinos.
In this paper, we present a forecast for the search for sterile neutrinos using joint GW-GRB observations. The primary aim of this work is to investigate the impact of future GW standard siren observations on the constraints of sterile neutrino parameters.
This work is organized as follows. In section 2 , we introduce the methodology used in this work. In section 3 , we give the constraint results and make some relevant discussions. The conclusion is given in section 4 .
2. Methodology
2.1. Gravitational wave simulation
The BNS merger rate with redshift in the observer frame is [136–138]
$\begin{eqnarray}{R}_{{\rm{m}}}(z)=\frac{{{ \mathcal R }}_{{\rm{m}}}(z)}{1+z}\frac{{\rm{d}}V(z)}{{\rm{d}}z},\end{eqnarray}$
where dV(z)/dz is the comoving volume element, the factor (1 + z)−1 converts the merger rate in the source frame to the observer frame, and ${{ \mathcal R }}_{{\rm{m}}}(z)$ is the BNS merger rate in the source frame, expressed as $\begin{eqnarray}{{ \mathcal R }}_{{\rm{m}}}(z)={\int }_{{t}_{{\rm{\min }}}}^{{t}_{{\rm{\max }}}}{{ \mathcal R }}_{{\rm{f}}}[t(z)-{t}_{{\rm{d}}}]P({t}_{{\rm{d}}}){\rm{d}}{t}_{{\rm{d}}},\end{eqnarray}$
which is commonly used in the literature [137–147]6. Here, td is the delay time between the formation of BNS system and merger, ${t}_{{\rm{\min }}}=20$ Myr is the minimum delay time, ${t}_{{\rm{\max }}}={t}_{{\rm{H}}}$ is the maximum delay time, t(z) is the age of the Universe at the time of merger, ${{ \mathcal R }}_{{\rm{f}}}$ is the cosmic star formation rate in the source frame for which we adopt the Madau–Dickinson model [149], P(td) is the time delay distribution of the td, and we adopt the exponential time delay model [136], which is given by $\begin{eqnarray}P({t}_{{\rm{d}}})=\frac{1}{\tau }{\rm{\exp }}(-{t}_{{\rm{d}}}/\tau ),\end{eqnarray}$
with an e-fold time of τ = 0.1 Gyr for ${t}_{{\rm{d}}}\gt {t}_{{\rm{\min }}}$.In our calculations, for BNS mergers, we consider the local comoving merger rate to be ${{ \mathcal R }}_{{\rm{m}}}(z=0)=920\,{\rm{G}}p{c}^{-3}\,y{r}^{-1}$, which is the estimated median from the O1 LIGO and the O2 LIGO/Virgo observation run [150] and is also consistent with the O3 observation run [151]. We simulate a catalog of BNS mergers for 10 years observation. For each source, the location (θ, φ), the polarization angle ψ, the cosine of the inclination angle ι, and the coalescence phase ψc are drawn from uniform distributions. Currently, there are multiple candidate models for the neutron star (NS) mass distribution. However, different mass distributions of NSs have less impact on the cosmological analysis [43]. For simplicity, we employ a Gaussian mass distribution. This distribution has a mean of 1.33M⊙ for the NS mass and a standard deviation of 0.09M⊙, where M⊙ represents the solar mass [152, 153].
Under the stationary phase approximation [154], the Fourier transform of the frequency-domain GW waveform for a detector network (with N detectors) is given by [155, 156]
$\begin{eqnarray}\tilde{{\boldsymbol{h}}}(f)={{\rm{e}}}^{{\rm{-i}}{\boldsymbol{\Phi }}}{\boldsymbol{h}}(f),\end{eqnarray}$
with the h(f) is given by $\begin{eqnarray}{\boldsymbol{h}}(f)={\left[\frac{{h}_{1}(f)}{\sqrt{{S}_{{\rm{n}},1}(f)}},\frac{{h}_{2}(f)}{\sqrt{{S}_{{\rm{n}},2}(f)}},\ldots ,\frac{{h}_{N}(f)}{\sqrt{{S}_{{\rm{n}},N}(f)}}\right]}^{{\rm{T}}},\end{eqnarray}$
where Φ is the N × N diagonal matrix with Φij = 2πfδij(n · rk), n is the propagation direction of GW, and rk is the location of the k-th detector. Here Sn,k(f) is the one-side noise power spectral density of the k-th detector, The Fourier transform of the GW waveform of k-th detector is given by $\begin{eqnarray}\begin{array}{rcl}{h}_{k}(f) & = & {{ \mathcal A }}_{k}{f}^{-7/6}{\rm{\exp }}\{{\rm{i}}[2\pi f{t}_{{\rm{c}}}-\pi /4-2{\psi }_{c}+2{\rm{\Psi }}(f/2)]\\ & & -\,{\varphi }_{k,(2,0)})\},\end{array}\end{eqnarray}$
where the Fourier amplitude can be written as $\begin{eqnarray}\begin{array}{rcl}{{ \mathcal A }}_{k} & = & \displaystyle \frac{1}{{d}_{{\rm{L}}}}\sqrt{{({F}_{+,k}(1+{\cos }^{2}\iota ))}^{2}+{(2{F}_{\times ,k}\cos \iota )}^{2}}\\ & & \times \sqrt{5\pi /96}{\pi }^{-7/6}{{ \mathcal M }}_{{\rm{chirp}}}^{5/6}.\end{array}\end{eqnarray}$
Here, the detailed forms of $\Psi$(f/2) and φk,(2,0) can be found in [155, 157], dL is the luminosity distance of the GW source, ${{ \mathcal M }}_{{\rm{chirp}}}=(1+z){\eta }^{3/5}M$ is the observed chirp mass, η = m1m2/M2 is the symmetric mass ratio, and M = m1 + m2 is the total mass of the binary system with component masses m1 and m2, F+,k and F×,k are the antenna response functions of the k-th GW detector, we adopt the GW waveform in the frequency-domain, in which the time t is replaced by ${t}_{{\rm{f}}}={t}_{{\rm{c}}}-(5/256){{ \mathcal M }}_{{\rm{chirp}}}^{-5/3}{(\pi f)}^{-8/3}$ [155, 157], where tc is the coalescence time.After simulating the GW catalog, we need to calculate the signal-to-noise ratio (SNR) for each GW event. The SNR for the detection network of N independent interferometers can be calculated by
$\begin{eqnarray}\rho ={(\tilde{{\boldsymbol{h}}}| \tilde{{\boldsymbol{h}}})}^{1/2}.\end{eqnarray}$
The inner product is defined as $\begin{eqnarray}({\boldsymbol{a}}| {\boldsymbol{b}})=2{\int }_{{f}_{{\rm{lower}}}}^{{f}_{{\rm{upper}}}}\{{\boldsymbol{a}}(f){{\boldsymbol{b}}}^{* }(f)+{{\boldsymbol{a}}}^{* }(f){\boldsymbol{b}}(f)\}{\rm{d}}f,\end{eqnarray}$
where * represents conjugate transpose, a and b are column matrices of the same dimension, the lower cutoff frequency is set to flower = 1 Hz for ET and flower = 5 Hz for CE, and fupper = 2/(63/22πMobs) is the frequency at the last stable orbit with Mobs = (m1 + m2)(1 + z). In this work, we adopt the SNR threshold to be 12 in our simulation.For the short GRB model, we adopt the model of Gaussian structured jet profile based on the GW170817/GRB170817A [159] observation,
$\begin{eqnarray}{L}_{{\rm{iso}}}({\theta }_{{\rm{v}}})={L}_{{\rm{on}}}\exp \left(-\displaystyle \frac{{\theta }_{{\rm{v}}}^{2}}{2{\theta }_{{\rm{c}}}^{2}}\right),\end{eqnarray}$
where θv is the viewing angle, Liso(θv) is the isotropically equivalent luminosity of short GRB observed at different θv, Lon = Liso(0) is the on-axis isotropic luminosity, θc = 4. 7∘ is the characteristic angle of the core, and the direction of the jet is assumed to align with the binary orbital angular momentum, namely ι = θv.For the distribution of the short GRB, we assume the empirical broken-power-law luminosity function7
$\begin{eqnarray}{\rm{\Phi }}(L)\propto \left\{\begin{array}{ll}{(L/{L}_{* })}^{\alpha }, & L\lt {L}_{* },\\ {(L/{L}_{* })}^{\beta }, & L\geqslant {L}_{* },\end{array}\right.\end{eqnarray}$
which is commonly used in the literature [38, 42, 43, 46, 137, 138, 146, 148]. Here, L is the isotropic rest frame luminosity in the 1 − 10000 keV energy range, L* is the characteristic luminosity that separates the low and high end of the luminosity function, and the slopes describing these regimes are given by α and β, respectively. Following [146], we adopt L* = 2 × 1052 erg sec−1, α = − 1.95, and β = − 3. We assume a standard low end cutoff in luminosity of ${L}_{{\rm{\min }}}=1{0}^{49}$ erg sec−1, and we also term the on-axis isotropic luminosity Lon as the peak luminosity L [43, 137, 138, 160]. For the THESEUS mission [161], a GRB detection is recorded if the value of observed flux is greater than the flux threshold PT = 0.2phs−1cm−2 in the 50-300 keV band. For the GRB detection, we assume a duty cycle of 80% and a sky coverage fraction of 0.5. From the GW catalogue which has passed the threshold 12, we can select the GW-GRB events according to the probability distribution Φ(L)dL.For a network with N independent interferometers, the Fisher information matrix is given by
$\begin{eqnarray}{F}_{ij}=\left(\left.\frac{\partial \tilde{{\boldsymbol{h}}}}{\partial {\theta }_{i}}\right|\frac{\partial \tilde{{\boldsymbol{h}}}}{\partial {\theta }_{j}}\right),\end{eqnarray}$
where θi denotes nine GW parameters (dL, ${{ \mathcal M }}_{{\rm{chirp}}}$, η, θ, φ, ι, tc, ψc, ψ) for a GW event.For the total uncertainty of the luminosity distance dL, we first consider the instrumental error ${\sigma }_{{d}_{{\rm{L}}}}^{{\rm{inst}}}$. The covariance matrix is equal to the inverse of the Fisher information matrix, thus the instrumental error of GW parameter θi is
$\begin{eqnarray}{\rm{\Delta }}{\theta }_{i}=\sqrt{{({F}^{-1})}_{ii}},\end{eqnarray}$
where Fij is the total Fisher information matrix for the network of N interferometers.In addition, the weak-lensing error ${\sigma }_{{d}_{{\rm{L}}}}^{{\rm{lens}}}$ and the peculiar velocity error ${\sigma }_{{d}_{{\rm{L}}}}^{{\rm{pv}}}$ are also considered. The error caused by weak lensing is adopted from [162, 163],
$\begin{eqnarray}\begin{array}{rcl}{\sigma }_{{d}_{{\rm{L}}}}^{{\rm{lens}}}(z) & = & \left[1-\frac{0.3}{\pi /2}\arctan (z/0.073)\right]\times {d}_{{\rm{L}}}(z)\\ & & \times 0.066{\left[\frac{1-{(1+z)}^{-0.25}}{0.25}\right]}^{1.8}.\end{array}\end{eqnarray}$
For the error caused by the peculiar velocity of the GW source is given by [164]
$\begin{eqnarray}{\sigma }_{{d}_{{\rm{L}}}}^{{\rm{pv}}}(z)={d}_{{\rm{L}}}(z)\times \left[1+\frac{c{(1+z)}^{2}}{H(z){d}_{{\rm{L}}}(z)}\right]\frac{\sqrt{\langle {v}^{2}\rangle }}{c},\end{eqnarray}$
where c is the speed of light in vacuum, H(z) is the Hubble parameter, and $\sqrt{\langle {v}^{2}\rangle }$ is the peculiar velocity of the GW source with respect to the Hubble flow is roughly set to $\sqrt{\langle {v}^{2}\rangle }=500\,{\rm{km}}{{\rm{s}}}^{-1}$.Hence, the total error of dL can be written as
$\begin{eqnarray}{\sigma }_{{d}_{{\rm{L}}}}=\sqrt{{({\sigma }_{{d}_{{\rm{L}}}}^{{\rm{inst}}})}^{2}+{({\sigma }_{{d}_{{\rm{L}}}}^{{\rm{lens}}})}^{2}+{({\sigma }_{{d}_{{\rm{L}}}}^{{\rm{pv}}})}^{2}}.\end{eqnarray}$
2.2. Other cosmological observations
For comparison, we also employ three current EM cosmological observations, i.e., the cosmic microwave background (CMB) data, the baryon acoustic oscillation (BAO) data, and the type Ia supernova (SN) data. The details of these data are listed as follows.
The CMB data: the CMB likelihood including the TT, TE, EE spectra at l ≥ 30, the low-l temperature commander likelihood, and the low-l SimAll EE likelihood, from the Planck 2018 data release [165].
The SN data: the Pantheon sample comprised of 1048 data points from the Pantheon compilation [169].
2.3. Methods of constraining cosmological parameters
In this paper, we will consider both cases of massless and massive sterile neutrinos in the framework of standard model (ΛCDM) of cosmology. For the ΛCDM model, the base parameter set (including six free parameters) is
$\begin{eqnarray*}{\bf{P}}=\{{\omega }_{b},\,{\omega }_{c},\,100{\theta }_{{\rm{MC}}},\,\tau ,\,\mathrm{ln}(1{0}^{10}{A}_{{\rm{s}}}),\,{n}_{{\rm{s}}}\},\end{eqnarray*}$
where ωb ≡ Ωbh2 and ωc ≡ Ωch2 are the physical densities of baryon and cold dark matter, respectively, θMC is the ratio (multiplied by 100) between the sound horizon and the angular diameter distance at the time of last-scattering, τ is the optical depth to the reionization, As is the amplitude of the primordial curvature perturbation, and ns is the scalar spectral index.When we consider massless sterile neutrinos (as the dark radiation) in the ΛCDM model, an additional parameter Neff (the effective number of relativistic species) need to be added in the model, and this case is called ΛCDM+Neff model in this paper. When the massive sterile neutrinos are considered in the ΛCDM model, two extra free parameters, the Neff and ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ (the effective sterile neutrino mass) need to be added in the model, and this case is called ΛCDM+Neff+${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ model in this paper. Thus, the ΛCDM+Neff model has seven independent parameters, and the ΛCDM+Neff+${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ has eight independent parameters. Note that in both the massless and massive sterile neutrino cases the total mass of active neutrinos is fixed at ∑mν = 0.06 eV.
For the GW standard siren observation with N data point, the χ2 function is defined as
$\begin{eqnarray}{\chi }_{{\rm{GW}}}^{2}=\displaystyle \sum _{i=1}^{N}{\left[\frac{{d}_{{\rm{L}}}^{i}-{d}_{{\rm{L}}}({z}_{i};\overrightarrow{{\rm{\Omega }}})}{{\sigma }_{{d}_{{\rm{L}}}}^{i}}\right]}^{2},\end{eqnarray}$
where zi, ${d}_{{\rm{L}}}^{i}$, and ${\sigma }_{{d}_{{\rm{L}}}}^{i}$ are the i-th GW redshift, luminosity distance, and the measurement error of the luminosity distance, respectively, $\overrightarrow{{\rm{\Omega }}}$ denotes the set of cosmological parameters.In this work, we present the first forecast for the search for sterile neutrinos using joint GW-GRB observation. We use the public Markov-chain Monte Carlo (MCMC) package CosmoMC [170] to constrain sterile neutrino and other cosmological parameters. To demonstrate the impact of simulated GW data on constraining sterile neutrino parameters, we will consider all the different cases of 3G GW observations, the single ET, the single CE, the CE-CE network (one CE in the United States with 40-km arm length and another one in Australia with 20-km arm length, abbreviated as 2CE hereafter), and the ET-CE-CE network (one ET detector and two CE-like detectors, abbreviated as ET2CE hereafter) to analysis. We utilize the sensitivity curves of ET from [171] and for CE from [172], as shown in figure 1. For the GW detector, in view of the high uncertainty of the duty cycle, we only calculate the ideal scenario assuming a 100% duty cycle for all detectors, as discussed in [173]. The specific parameters characterizing the geometry of GW detector (latitude φ, longitude λ, opening angle ζ, and arm bisector angle γ) are detailed in table 1. The number of GW standard sirens in the subsequent cosmological analysis are shown in table 2 and their redshift distributions are shown in figure 2.
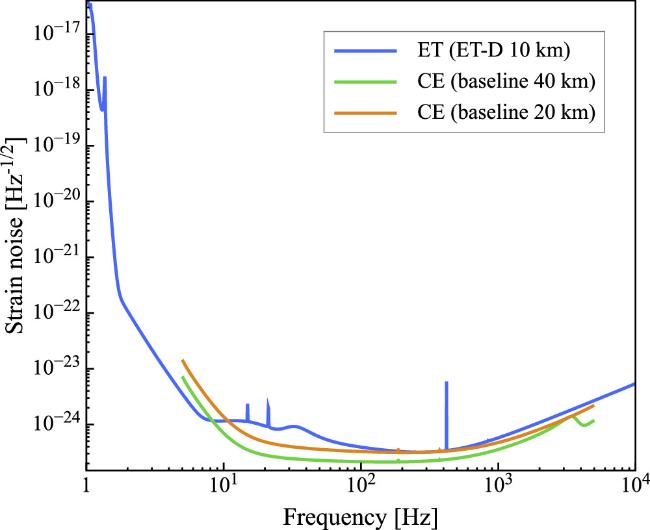
Figure 1. Sensitivity curves of the 3G GW detectors considered in this work. |
Table 1. The specific coordinate parameters considered in this work. |
| GW detector | φ(deg) | λ(deg) | γ(deg) | ζ(deg) |
|---|---|---|---|---|
| Einstein Telescope, Europe | 40.443 | 9.457 | 0.000 | 60 |
| Cosmic Explorer, USA | 43.827 | −112.825 | 45.000 | 90 |
| Cosmic Explorer, Australia | −34.000 | 145.000 | 90.000 | 90 |
Table 2. Numbers of GW standard sirens in cosmological analysis, triggered by THESEUS in synergy with ET, CE, 2CE, and ET2CE, respectively. |
| Detection strategy | ET | CE | 2CE | ET2CE |
|---|---|---|---|---|
| Number of GW standard sirens | 400 | 538 | 600 | 640 |
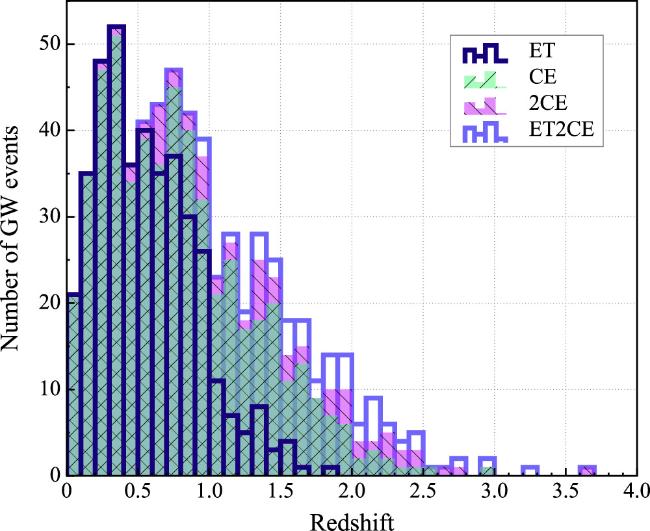
Figure 2. Redshift distributions of BNS detected by THESEUS in synergy with ET, CE, 2CE, and ET2CE for a 10-year observation. |
The primary goal of this work is to assess the influence of joint observations between 3G GW detectors and future GRB detectors on the cosmological measurement of sterile neutrino parameters. Such observations are crucial for alleviating the degeneracies in cosmological parameters that are commonly observed in traditional EM data. To elucidate this, we have conducted simulations to generate mock GW data, which we have subsequently integrated with the mainstream EM observations, i.e., CMB+BAO+SN data. Our analysis specifically focuses on the estimation errors and precision of sterile neutrino parameters derived from this combined dataset.
To avoid any inconsistencies in the cosmological parameters constrained by combining CMB+BAO+SN with GW mock data, we have adopted a strategic approach. This approach is designed to thoroughly investigate the capacity of GW mock data to break the parameter degeneracies present in conventional EM observations. For this purpose, we have utilized the best-fit values of the cosmological parameters derived from the CMB+BAO+SN dataset as the reference values for simulating the GW mock data corresponding to each cosmological model. This methodology enables a more accurate assessment of the role of GW data in enhancing the precision of parameter estimation and resolving the degeneracies encountered in traditional EM observations.
For simplicity, we use 'CBS' to denote the joint CMB+BAO+SN data combination. Thus, in our analysis, we use five data combinations: (1) CBS, (2) CBS+ET, (3) CBS+CE, (4) CBS+2CE, and (5) CBS+ET2CE. We will report the constraint results in the next section.
3. Results and discussion
In this section, we report the constraint results for the ΛCDM+Neff and ΛCDM+Neff+${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ models using the CBS, CBS+ET, CBS+CE, CBS+2CE, and CBS+ET2CE data combinations and analyze how the GW standard sirens affect the cosmological constraints on the sterile neutrino parameters. The fitting results are shown in figures 3 and 4 and in tables 3 and 4. In the tables, we quote ± 1σ errors for the parameters, but for the parameters that cannot be well constrained, e.g., the sterile neutrino parameters Neff and ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$, we quote the 2σ upper limits. For a parameter ξ, we use σ(ξ) and ϵ(ξ) = σ(ξ)/ξ to represent its absolute error and relative error, respectively.
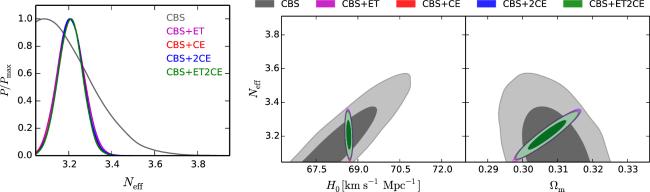
Figure 3. Constraint results for the ΛCDM+Neff model from the CBS, CBS+ET, CBS+CE, CBS+2CE, and CBS+ET2CE data combinations. One-dimensional marginalized posterior distribution for Neff (left panel), and two-dimensional marginalized posterior contours (1σ and 2σ) in the H0–Neff and Ωm–Neff planes (right panel). |
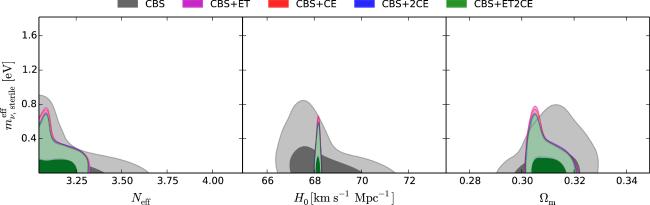
Figure 4. Two-dimensional marginalized posterior contours (1σ and 2σ) in the Neff–${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$, H0–${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$, Ωm–${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ planes for the ΛCDM+Neff+${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ model from the constraints of the CBS, CBS+ET, CBS+CE, CBS+2CE, and CBS+ET2CE data combinations. |
Table 3. Fitting results of the ΛCDM+Neff model by using the CBS, CBS+ET, CBS+CE, CBS+2CE, and CBS+ET2CE data combinations. We quote ± 1σ errors for the parameters, but for the parameters that cannot be well constrained, we quote the 2σ upper limits. Here, H0 is in units of kms−1 Mpc−1. |
| Model | CBS | CBS+ET | CBS+CE | CBS+2CE | CBS+ET2CE |
|---|---|---|---|---|---|
| Ωbh2 | 0.02247 ± 0.00015 | 0.02248 ± 0.00011 | 0.02248 ± 0.00011 | 0.02248 ± 0.00011 | 0.02248 ± 0.00011 |
| Ωch2 | $0.122{0}_{-0.0028}^{+0.0017}$ | 0.1217 ± 0.0017 | 0.1217 ± 0.0016 | 0.1217 ± 0.0016 | 0.1217 ± 0.0016 |
| 100θMC | $1.0404{6}_{-0.00037}^{+0.00043}$ | 1.04050 ± 0.00036 | $1.0405{0}_{-0.00035}^{+0.00034}$ | 1.04049 ± 0.00035 | 1.04050 ± 0.00034 |
| τ | $0.055{8}_{-0.0083}^{+0.0074}$ | $0.055{8}_{-0.0082}^{+0.0075}$ | $0.055{9}_{-0.0082}^{+0.0074}$ | $0.055{9}_{-0.0082}^{+0.0075}$ | $0.055{8}_{-0.0082}^{+0.0072}$ |
| ns | $0.969{7}_{-0.0057}^{+0.0046}$ | 0.9696 ± 0.0030 | $0.969{6}_{-0.0031}^{+0.0030}$ | 0.9697 ± 0.0030 | 0.9697 ± 0.0029 |
| ${\rm{ln}}(1{0}^{10}{A}_{s})$ | $3.05{1}_{-0.018}^{+0.016}$ | 3.050 ± 0.016 | 3.050 ± 0.016 | 3.050 ± 0.016 | 3.050 ± 0.016 |
| σ8 | $0.817{7}_{-0.0101}^{+0.0083}$ | $0.817{0}_{-0.0081}^{+0.0082}$ | 0.8169 ± 0.0078 | 0.8171 ± 0.0079 | 0.8169 ± 0.0077 |
| Ωm | $0.307{7}_{-0.0061}^{+0.0060}$ | 0.3071 ± 0.0038 | $0.307{1}_{-0.0036}^{+0.0035}$ | 0.3071 ± 0.0035 | $0.307{0}_{-0.0035}^{+0.0034}$ |
| H0 | $68.67{0}_{-1.020}^{+0.640}$ | $68.67{1}_{-0.055}^{+0.057}$ | $68.67{1}_{-0.057}^{+0.056}$ | $68.67{1}_{-0.054}^{+0.052}$ | $68.67{2}_{-0.050}^{+0.052}$ |
| Neff | < 3.464 | 3.209 ± 0.060 | 3.209 ± 0.056 | $3.21{0}_{-0.056}^{+0.055}$ | $3.20{8}_{-0.055}^{+0.054}$ |
| | |||||
| ΔNeff > 0 | . . . | 2.717σ | 2.911σ | 2.929σ | 2.945σ |
| σ(Ωm) | 0.00605 | 0.00380 | 0.00355 | 0.00350 | 0.00345 |
| σ(H0) | 0.8300 | 0.0560 | 0.0565 | 0.0530 | 0.0510 |
| ϵ(Ωm) | 1.966% | 1.237% | 1.156% | 1.140% | 1.124% |
| ϵ(H0) | 1.209% | 0.082% | 0.082% | 0.077% | 0.074% |
Table 4. Fitting results of the ΛCDM+${N}_{{\rm{eff}}}+{m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ model by using the CBS, CBS+ET, CBS+CE, CBS+2CE, and CBS+ET2CE data combinations. We quote ± 1σ errors for the parameters, but for the parameters that cannot be well constrained, we quote the 2σ upper limits. Here, H0 is in units of kms−1Mpc−1 and ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ is in units of eV. |
| Model | CBS | CBS+ET | CBS+CE | CBS+2CE | CBS+ET2CE |
|---|---|---|---|---|---|
| Ωbh2 | $0.0224{7}_{-0.00016}^{+0.00015}$ | 0.02249 ± 0.00012 | 0.02249 ± 0.00012 | 0.02249 ± 0.00012 | 0.02249 ± 0.00012 |
| Ωch2 | $0.119{8}_{-0.0031}^{+0.0036}$ | $0.119{3}_{-0.0018}^{+0.0033}$ | $0.119{3}_{-0.0017}^{+0.0032}$ | $0.119{5}_{-0.0017}^{+0.0031}$ | $0.119{4}_{-0.0017}^{+0.0030}$ |
| 100θMC | $1.0405{9}_{-0.00033}^{+0.00047}$ | $1.0407{1}_{-0.00035}^{+0.00041}$ | $1.0407{1}_{-0.00035}^{+0.00040}$ | $1.0407{0}_{-0.00036}^{+0.00040}$ | $1.0407{1}_{-0.00036}^{+0.00039}$ |
| τ | $0.056{1}_{-0.0083}^{+0.0073}$ | $0.056{6}_{-0.0082}^{+0.0074}$ | $0.056{6}_{-0.0082}^{+0.0074}$ | $0.056{8}_{-0.0083}^{+0.0074}$ | $0.056{9}_{-0.0083}^{+0.0074}$ |
| ns | $0.968{1}_{-0.0065}^{+0.0047}$ | 0.9684 ± 0.0033 | 0.9684 ± 0.0033 | 0.9684 ± 0.0033 | $0.968{4}_{-0.0032}^{+0.0033}$ |
| ${\rm{ln}}(1{0}^{10}{A}_{s})$ | $3.04{8}_{-0.018}^{+0.016}$ | $3.04{8}_{-0.017}^{+0.016}$ | $3.04{8}_{-0.017}^{+0.016}$ | 3.048 ± 0.016 | 3.048 ± 0.016 |
| σ8 | $0.79{6}_{-0.014}^{+0.024}$ | $0.79{5}_{-0.012}^{+0.022}$ | $0.79{5}_{-0.012}^{+0.022}$ | $0.79{6}_{-0.012}^{+0.021}$ | $0.79{6}_{-0.012}^{+0.022}$ |
| Ωm | 0.3114 ± 0.0064 | $0.309{6}_{-0.0052}^{+0.0032}$ | $0.309{6}_{-0.0050}^{+0.0032}$ | $0.309{7}_{-0.0049}^{+0.0033}$ | $0.309{6}_{-0.0048}^{+0.0033}$ |
| H0 | $68.15{0}_{-1.000}^{+0.500}$ | $68.15{6}_{-0.053}^{+0.055}$ | $68.15{6}_{-0.053}^{+0.054}$ | $68.15{6}_{-0.053}^{+0.054}$ | $68.15{6}_{-0.050}^{+0.054}$ |
| Neff | < 3.446 | $3.14{8}_{-0.094}^{+0.039}$ | $3.14{8}_{-0.090}^{+0.040}$ | $3.15{0}_{-0.089}^{+0.043}$ | $3.15{0}_{-0.089}^{+0.042}$ |
| ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ | < 0.5789 | < 0.4842 | < 0.4772 | < 0.4321 | < 0.4226 |
| | |||||
| ΔNeff > 0 | ... | 1.085σ | 1.133σ | 1.169σ | 1.169σ |
| σ(Ωm) | 0.00640 | 0.00420 | 0.00410 | 0.00410 | 0.00405 |
| σ(H0) | 0.7500 | 0.0540 | 0.0535 | 0.0535 | 0.0520 |
| ϵ(Ωm) | 2.055% | 1.357% | 1.324% | 1.324% | 1.308% |
| ϵ(H0) | 1.101% | 0.079% | 0.078% | 0.078% | 0.076% |
In accordance with the cosmological parameter constraints obtained from the CBS data, the central values and uncertainties of the cosmological parameters from the combined CBS and GW observations are detailed in tables 3 and 4. Given that the CBS data is real, whereas the GW data is simulated, the constraints from the joint CBS and GW analysis represent a mixture of real and simulated data. Consequently, the central values should not be interpreted as from actual observational data. As such, this work emphasizes the significance of the uncertainties and precision in the derived cosmological constraints.
3.1. The case of massless sterile neutrino
The massless sterile neutrinos serve as the dark radiation, and thus in this case Neff is treated as a free parameter, the total relativistic energy density of radiation is given by
$\begin{eqnarray}{\rho }_{{\rm{r}}}=\left[1+{N}_{{\rm{eff}}}\frac{7}{8}{\left(\frac{4}{11}\right)}^{\frac{4}{3}}\right]{\rho }_{\gamma },\end{eqnarray}$
where ργ is the photon energy density. In the ΛCDM model, Neff = 3.046, and so ΔNeff = Neff − 3.046 > 0 indicates the presence of extra relativistic particle species in the early universe, and in this paper we take the fit results of ΔNeff > 0 as evidence of the existence of massless sterile neutrinos.In table 3, we find that the CBS data provides only an upper limit, Neff < 3.464, indicating that the existence of massless sterile neutrinos is not favored by the CBS data. However, when GW standard sirens are included in the data combination, the results change significantly. After considering the GW data, we obtain Neff = 3.209 ± 0.060 for CBS+ET, Neff = 3.209 ± 0.056 for CBS+CE, ${N}_{{\rm{eff}}}=3.21{0}_{-0.056}^{+0.055}$ for CBS+2CE, and ${N}_{{\rm{eff}}}=3.20{8}_{-0.055}^{+0.054}$ for CBS+ET2CE, which indicates a detection of ΔNeff > 0 at the 2.717σ, 2.911σ, 2.929σ, and 2.945σ significance levels, respectively. Obviously, the GW data can indeed effectively improve the constraints on the massless sterile neutrino parameter Neff.
Note that here CBS refers to current real observational data, while GW denotes simulated data. When we use the actual CBS data to conduct constraints, we can only obtain an upper limit for Neff and not a definitive detection result. However, when simulated GW data is included, the errors in the parameter constraints are significantly reduced. With the central value of Neff remaining essentially unchanged and ΔNeff substantially decreased, we can achieve a result of ΔNeff > 0. Our results indicate that future GW observations can greatly assist in improving the cosmological detection of massless sterile neutrinos, with a significance level reaching up to 3σ. Of course, we must remember that our findings are based on simulated outcomes, and the central value of Neff is set to be consistent with the result from CBS.
In the right panel of figure 3, we show the two-dimensional posterior distribution contours (1σ and 2σ) in the Neff–H0 and Neff–Ωm planes for the ΛCDM+Neff model using CBS, CBS+ET, CBS+CE, CBS+2CE, and CBS+ET2CE data combinations. We can see that Neff is in positive correlation with H0 by using the CBS data combination. However, after adding the GW data, this correlation becomes negligible, indicating that the degeneracy between Neff and H0 is effectively broken by the GW observations. In addition, we can also clearly see that when considering the GW data, the parameter space is greatly shrunk in each plane and the constraints on cosmological parameters of H0 and Ωm become much tighter.
In table 3, we also show absolute and relative errors of H0 and Ωm from the CBS, CBS+ET, CBS+CE, CBS+2CE, and CBS+ET2CE data combinations. Compared to the CBS data, we find that the accuracy of the H0 constraint improves by 93.253% for CBS+ET, 93.193% for CBS+CE, 93.614% for CBS+2CE, and 93.855% for CBS+ET2CE, respectively. Similarly, the accuracy of the Ωm constraint improves by 37.190% for CBS+ET, 41.322% for CBS+CE, 42.149% for CBS+2CE, and 42.975% for CBS+ET2CE, respectively. Obviously, the GW data can indeed effectively improve the constraints on the parameters H0 and Ωm.
3.2. The case of massive sterile neutrino
In this subsection, we investigated how GW standard sirens constrain the massive sterile neutrino parameters. Hence, the requirement of Neff > 3.046 still holds.
From table 4, we obtain Neff < 3.446 by using CBS data. After adding the GW data, the constraint results become ${N}_{{\rm{eff}}}=3.14{8}_{-0.094}^{+0.039}$ for CBS+ET, ${N}_{{\rm{eff}}}=3.14{8}_{-0.090}^{+0.039}$ for CBS+CE, ${N}_{{\rm{eff}}}=3.15{0}_{-0.089}^{+0.043}$ for CBS+2CE, and ${N}_{{\rm{eff}}}=3.15{0}_{-0.089}^{+0.042}$ for CBS+ET2CE, respectively. We find that Neff cannot be well constrained using the CBS data, but the addition of GW data can significantly improve the constraint on Neff, favoring ΔNeff > 0 at 1.085σ (CBS+ET), 1.133σ (CBS+CE), 1.169σ (CBS+2CE), and 1.169σ (CBS+ET2CE) statistical significance, respectively. For the mass of sterile neutrino, the CBS data give ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}\lt 0.5789$ eV and further including the GW data leads to results of ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}\lt 0.4842$ eV (CBS+ET), ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}\lt 0.4772$ eV (CBS+CE), ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}\lt 0.4321$ eV (CBS+2CE), and ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}\lt 0.4226$ eV (CBS+ET2CE), respectively. Evidently, adding GW data tightens the constraint on ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ significantly, which is in accordance with the conclusions in previous studies' active neutrinos mass by using the GW data [14, 37, 46]. Therefore, the GW data also plays an important role in constraining the mass of sterile neutrinos.
In figure 4, we show two-dimensional marginalized posterior contours (1σ and 2σ) in the Neff–${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$, H0–${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$, Ωm–${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ planes for the ΛCDM+Neff+${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ model. We can clearly see that when further considering the GW data, the parameter space is also greatly shrunk and the constraints on H0 and Ωm also become much tighter. From table 4, we find that the constraints on H0 and Ωm could be improved by 92.800% and 34.375%, respectively, when adding the ET data to the CBS data, 92.867% and 35.938% for the case of CE, 92.867% and 35.938% for the case of 2CE, and 93.067% and 36.719% for the case of ET2CE, respectively. These results are in accordance with the conclusions for both the case of massless sterile neutrinos in this study and active neutrinos mass in previous studies [14, 37, 46]. Therefore, the inclusion of GW data can significantly improve constraints on most cosmological parameters, particularly H0 and Ωm.
4. Conclusion
This work aims to forecast the search for sterile neutrinos using joint GW-GRB observations. We consider two cases of massless and massive sterile neutrinos, corresponding to the ΛCDM+Neff and ΛCDM+Neff+${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ models, respectively. We consider four GW detection observation strategies, i.e., ET, CE, the 2CE network, and the ET2CE network, to perform cosmological analysis. To evaluate the impact of GW data on the constraints of sterile neutrino parameters, we also considered existing CMB+BAO+SN data for comparison and combination.
For the ΛCDM+Neff model, in the case of using CMB+BAO+SN, only upper limits on Neff can be obtained. Further adding the GW data tightens the Neff significantly, and in this case the preference of ΔNeff > 0 at about 3σ level. Therefore, GW standard siren observations can greatly assist in the detection of massless sterile neutrinos.
For the ΛCDM+Neff+${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ model, only upper limits on Neff and ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ can be derived by using the CMB+BAO+SN data. Further including GW data significantly improves the constraints, and we find that the GW data gives a rather tight upper limit on ${m}_{\nu ,{\rm{sterile}}}^{{\rm{eff}}}$ and favor ΔNeff > 0 at about 1.1σ level. These results also seem to favor massless sterile neutrinos.
Furthermore, we find that the GW data can significantly enhance the accuracy of constraints on the derived parameters H0 and Ωm. The accuracy of H0 improves by approximately 93% and the accuracy of Ωm increases by about 37% to 42%, when the GW data is included in the cosmological fit.