1. Introduction
The critical phenomena and critical exponents have been extensively investigated over many decades, using the φ4 (or Ginzburg–Landau) model as one of the basic models for analytical [1–7], as well as numerical [8–14] studies. We consider the local order parameter φ as a scalar or, more generally, an N-component vector. In the latter case, this φ4 model is known also as the O(N) model, pointing to its rotational symmetry. It represents the most celebrated example of universality [14], which describes the critical properties of a wide range of physical phase transitions, such as ferromagnetic and antiferromagnetic, liquid-vapor, as well as superconducting and superfluid transitions.
The scalar φ4 model belongs to the Ising universality class. The Ising model is more convenient for numerical studies than the φ4 model, therefore most of the numerical results for this universality class come just from the Ising model. The critical exponents of the 2D Ising model are known exactly [15, 16]. Hence, the numerical studies have been mainly focused on the 3D case, including Monte Carlo (MC) simulations [17–19], high temperature (HT) series expansion [20–22] and the conformal bootstrap calculations [23–26].
Although the 2D Ising model is well studied, we have found that the 2D case of the scalar φ4 model is very intriguing, which requires further investigation. A point here is that the 2D φ4 model might contain non-trivial corrections to scaling, which do not show up or vanish in the 2D Ising model, as regards a subset of quantities, including the moments of magnetization and energy per spin, as well as other related quantities. This possibility has been pointed out in our earlier study [11], based on MC simulations and some analytical arguments. Historically, several results have been obtained for the correction-to-scaling exponent ω in the 2D φ4 model, which differ from ω = 2 which is usually observed in the 2D Ising model. In particular, ω = 4/3 has been conjectured in [3], based on the perturbative renormalization group (RG) calculations. Later, this discrepancy with ω = 2 has been explained in [27], suggesting that the Callan–Symanzik β-function, used in these RG calculations, is singular at the fixed point. However, recent results of the ε-expansion, which do not use this β-function, also give a value that is somewhat smaller than 2 of ω, i.e., ω = 1.71(10) [7].
Non-integer correction-to-scaling exponents appear in the 2D Ising model, considering a wider set of quantities. In particular, the fractal geometry of the critical Potts clusters has been studied in [28] within the framework of RG and Coulomb gas approach, considering the fractal dimensions DM, DH, DEP and DSC, describing the scaling of the cluster's mass, hull, externally accessible perimeter and singly connected bonds, respectively, with its radius of gyration R. It has been found that the scaling corrections for the effective fractal dimensions are described by certain exponents θ, $\theta ^{\prime} $, θ″ and 1. As mentioned in [28], it is reasonable to interpret $\theta ^{\prime} $ and θ″ as the scaling exponents of some irrelevant perturbations in the spirit of the renormalization group. Hence, these correction exponents can also affect other quantities. The exact values of θ and $\theta ^{\prime} $ in the q-state Potts model at q = 2, i.e., in the Ising model, are $\theta =\theta ^{\prime} =4/3$ [28]. In view of these arguments, the correction-to-scaling exponent 4/3 can generally exist in the models of the 2D Ising universality class, including the 2D φ4 model. Moreover, the coincidence of the two exponents θ and $\theta ^{\prime} $ is a special case, therefore one may look for possible logarithmic corrections.
In the current work, we have performed much more accurate (longer) MC simulations than those in [11] to estimate ω in the case of pure power-law corrections to scaling, as well as to test the influence of logarithmic corrections and consistency with the exponent ω = 4/3, with and without the logarithmic corrections. As a result, we have found ω = 1.509(14) as our best estimate at the assumption of pure power-law corrections. This value is shifted to ω ≈ 7/4, assuming the logarithmic correction of the form $\mathrm{ln}L$, and to ω ≈ 4/3, assuming the $1/\mathrm{ln}L$ correction. In any way, these values appear to be somewhat surprising from the point of view of our earlier scaling arguments and analysis [11], where the existence of a correction-to-scaling with exponent 3/4 was expected. Hence, it served as a basis for a reconsideration of our earlier scaling assumptions. More flexible scaling assumptions allowed us to resolve this issue, as well as to correct and refine the analysis by the grouping of Feynman diagrams initiated in [6].
The paper is organized as follows. The results of the MC simulation are reported in section 2 . The estimation of ω from our MC data and the comparison with some of the known results are provided in section 3 . A critical reconsideration of the scaling arguments in [11] is provided in section 4 , and the related renewed analysis by the grouping of Feynman diagrams is considered in section 5 . Finally, the summary and discussion is given in section 6 .
2. MC simulation results for the lattice φ4 model
We have performed MC simulations of the 2D φ4 model on square lattice with periodic boundary conditions. The Hamiltonian ${ \mathcal H }$ is given by
$\begin{eqnarray}\frac{{ \mathcal H }}{{k}_{{\rm{B}}}T}=-\beta \displaystyle \sum _{\langle ij\rangle }{\varphi }_{i}{\varphi }_{j}+\displaystyle \sum _{i}\left({\varphi }_{i}^{2}+\lambda {\left({\varphi }_{i}^{2}-1\right)}^{2}\right),\end{eqnarray}$
where T is the temperature kB is the Boltzmann constant, − ∞ < φi < ∞ is a continuous scalar order parameter at the i-th lattice site, and ⟨ij⟩ denotes the set of all nearest neighbors. Here, we use the same notations as in our earlier MC study of this model [11], related to those in [29] via β = 2κ and φ = φ. The simulations have been performed by the hybrid algorithm, where cluster updates are combined with Metropolis sweeps, as described in [11, 29]. In our simulations, one step of the hybrid algorithm consisted of one Metropolis sweep and NW clusters of the Wolff algorithm. The parameter NW was chosen in such a way to ensure that the entire number of spin moves in NW clusters is about 2/3 or 0.6 of the total number of spins.The simulations in [11] have been performed at λ = 0.1, λ = 1 and λ = 10 at pseudocritical couplings ${\widetilde{\beta }}_{c}(L)$, corresponding to $U=\langle {m}^{4}\rangle /{\langle {m}^{2}\rangle }^{2}=1.1679229\approx {U}^{* }$ and U = 2, where m is the magnetization per spin, 1 − U/3 is the Binder cumulant, and U* is the known critical value of U found in [30]. Here we have performed extended simulations at λ = 0.1, making them significantly longer and extending the range of linear lattice sizes from L ≤ 1536 to L ≤ 2048. In [11], the results for each lattice size have been obtained from 100 simulation bins (iterations), each consisting of 106 hybrid algorithm steps. Here, in the extended simulations, the latter number is increased to 3 · 106 steps, the number of simulation bins being chosen as 300 for L ∈ [6, 384], 200 for L = 512, 100 for L ∈ [768, 1536] and 120 for L = 2048. The final results for the overlapping lattice sizes within L ≤ 1536 have been obtained by a weighted averaging of the actual MC values and those in [11], applying the weight coefficients proportional to the simulation length (the number of MC steps). The results for the normalized susceptibility χ/L7/4 (where χ = L2⟨m2⟩) and the normalized derivative − (∂U/∂β)/L are collected in table 1 and 2 at pseudocritical couplings ${\widetilde{\beta }}_{c}(L)$, corresponding to U = U* and U = 2, respectively. The normalization used here ensures that these quantities tend to certain finite values at L → ∞, in accordance with the known critical exponents γ = 7/4 and ν = 1 of the 2D Ising universality class.
Table 1. The values of ${\widetilde{\beta }}_{c}(L)$, χ/L7/4 and − (∂U/∂β)/L for λ = 0.1 and U = 1.1679229 ≈ U* depending on the lattice size L. |
| L | ${\widetilde{\beta }}_{c}$ | χ/L7/4 | − (∂U/∂β)/L |
|---|---|---|---|
| 6 | 0.6310451(76) | 1.92054(13) | 0.86991(19) |
| 8 | 0.6205904(55) | 1.70513(11) | 0.91937(19) |
| 12 | 0.6126206(35) | 1.494396(97) | 0.98891(23) |
| 16 | 0.6097694(27) | 1.394495(83) | 1.03316(23) |
| 24 | 0.6077895(17) | 1.302878(78) | 1.08511(27) |
| 32 | 0.6071420(14) | 1.261811(75) | 1.11200(29) |
| 48 | 0.60673002(87) | 1.226245(65) | 1.14005(32) |
| 64 | 0.60660154(68) | 1.210966(61) | 1.15320(34) |
| 96 | 0.60652379(44) | 1.198190(59) | 1.16602(37) |
| 128 | 0.60650059(31) | 1.192741(53) | 1.17128(36) |
| 192 | 0.60648656(21) | 1.188314(50) | 1.17676(38) |
| 256 | 0.60648299(17) | 1.186707(47) | 1.17978(37) |
| 384 | 0.60648037(11) | 1.185094(49) | 1.18112(38) |
| 512 | 0.606479833(90) | 1.184499(54) | 1.18115(45) |
| 768 | 0.606479199(84) | 1.183966(72) | 1.18249(67) |
| 1024 | 0.606479261(66) | 1.183828(71) | 1.18258(72) |
| 1536 | 0.606479163(42) | 1.183637(62) | 1.18270(72) |
| 2048 | 0.606479052(31) | 1.183539(72) | 1.18202(76) |
Table 2. The same quantities as in table 1 for λ = 0.1 and U = 2. |
| L | ${\widetilde{\beta }}_{c}$ | χ/L7/4 | − (∂U/∂β)/L |
|---|---|---|---|
| 6 | 0.5622957(89) | 0.500854(71) | 2.50489(62) |
| 8 | 0.5705578(64) | 0.446877(65) | 2.54550(65) |
| 12 | 0.5804632(43) | 0.394622(60) | 2.59107(77) |
| 16 | 0.5861528(33) | 0.370388(59) | 2.61472(77) |
| 24 | 0.5924095(22) | 0.349474(55) | 2.64609(86) |
| 32 | 0.5957579(16) | 0.341174(51) | 2.66479(96) |
| 48 | 0.5992428(11) | 0.335385(49) | 2.68905(95) |
| 64 | 0.60102839(66) | 0.333833(43) | 2.70895(94) |
| 96 | 0.60283621(49) | 0.333458(43) | 2.7284(10) |
| 128 | 0.60374599(36) | 0.333854(45) | 2.7382(11) |
| 192 | 0.60465782(23) | 0.334880(38) | 2.7563(11) |
| 256 | 0.60511400(17) | 0.335550(37) | 2.7625(11) |
| 384 | 0.60556994(12) | 0.336520(36) | 2.7729(11) |
| 512 | 0.60579760(11) | 0.336986(45) | 2.7772(15) |
| 768 | 0.606024909(96) | 0.337482(55) | 2.7827(20) |
| 1024 | 0.606138639(68) | 0.337825(56) | 2.7831(19) |
| 1536 | 0.606252317(45) | 0.338269(48) | 2.7885(18) |
| 2048 | 0.606308994(35) | 0.338425(52) | 2.7904(21) |
3. MC estimation of the correction-to-scaling exponent ω
3.1. Estimations from the susceptibility data
According to the finite-size scaling theory, the susceptibility behaves as χ ∝ Lγ/νf(L/ξ) for large L in the vicinity of the critical point, where ξ is the correlation length and f(L/ξ) is the scaling function. This is the leading asymptotic behavior, but we are particularly interested in corrections to scaling. There are generally (at arbitrary spatial dimension d) non-analytical corrections to scaling, which are by a factor ${ \mathcal O }\left({L}^{-\omega }\right)$ smaller than the leading term, ω being the leading correction-to-scaling exponent, as well as multiplicative and additive analytical corrections. The multiplicative analytical correction can be represented by the correction factor $1+{ \mathcal O }(t)$, where t = (βc − β)/βc is the reduced temperature and βc is the critical coupling, whereas the additive analytical correction represents an analytical background contribution. Noting that ${\widetilde{\beta }}_{c}(L)-{\beta }_{c}\unicode{x0007E}{L}^{-1/\nu }$ holds for the pseudocritical coupling at U = 2, we have ${ \mathcal O }(t)\unicode{x0007E}{L}^{-1/\nu }$ in this scaling regime. The case U = U* is special, where the amplitude at L−1/ν vanishes. These scaling considerations are consistent with the fact that U = F(tL1/ν) holds asymptotically with some regular scaling function F [17], and U* = F(0). In the first approximation, the additive analytical background contribution can be approximated by a constant value χ0, determined at t = 0 in the thermodynamic limit. Hence, by neglecting corrections of higher orders, the normalized susceptibility of the 2D φ4 model at $\beta ={\widetilde{\beta }}_{c}(L)$ can be approximated as 1 .
$\begin{eqnarray}\chi /{L}^{7/4}=A+B{L}^{-\omega }+C{L}^{-1}+{\chi }_{0}{L}^{-7/4},\end{eqnarray}$
noting that C = 0 holds at U = U*. This ansatz assumes pure power-law corrections and should be modified as $\begin{eqnarray}\chi /{L}^{7/4}=A+B{L}^{-\omega }\,{(\mathrm{ln}L)}^{\kappa }+C{L}^{-1}+{\chi }_{0}{L}^{-7/4},\end{eqnarray}$
with κ = 0, ± 1 to include possible logarithmic corrections discussed in section We start our analysis with the test of the pure power-law scenario (κ = 0), setting χ0 to zero at the beginning. The validity of such fits is confirmed a posteriori, as they provide stable results with ω < 7/4, implying that χ0L−7/4 is a smaller term than BL−ω at L → ∞. In the case of U = U*, it reduces to three-parameter fits to the ansatz χ/L7/4 = A + BL−ω. The results for ω, obtained by such fitting over the range of sizes $L\in [{L}_{{\rm{\min }}},2048]$, are shown in table 3 depending on ${L}_{{\rm{\min }}}$. The quality of fits is controlled by the value of χ2/d.o.f. (χ2 of the fit per degree of freedom), as well as by the goodness Q [31]. A smaller χ2/d.o.f. and a larger Q (where 0 < Q < 1) implies a higher quality of the fit, noting that χ2/d.o.f. is about unity for moderately good fits, and fits with Q > 0.1 are usually considered as acceptable. According to these criteria, the fits with ${L}_{{\rm{\min }}}$ from 64 to 128 in table 3 are acceptable. The corresponding values of ω agree within the error bars. We assume the estimate ω = 1.546(24) at ${L}_{{\rm{\min }}}=128$ as the best one, as it has a significantly smaller χ2/d.o.f. and larger Q values than in other cases, noting that further increasing of ${L}_{{\rm{\min }}}$ only increases the statistical errors bars without improvement of the fit quality.
Table 3. The MC estimates of ω, obtained by fitting the susceptibility data in table 1 to the ansatz χ/L7/4 = A + BL−ω within $L\in [{L}_{{\rm{\min }}},2048]$. The quality of these fits is controlled by the χ2/d.o.f. and the goodness Q values in the last two columns. |
| ${L}_{{\rm{\min }}}$ | ω | χ2/d.o.f. | Q |
|---|---|---|---|
| 32 | 1.5124(27) | 7.92 | 7 · 10−12 |
| 48 | 1.5454(50) | 1.85 | 0.055 |
| 64 | 1.5567(78) | 1.61 | 0.115 |
| 96 | 1.577(16) | 1.52 | 0.154 |
| 128 | 1.546(24) | 1.34 | 0.237 |
In the case of U = 2, the ansatz χ/L7/4 = A + BL−ω does not provide acceptable fits because χ/L7/4 is a nonmonotonous function of L, as it can be seen from table 2. The inclusion of the expected, in this case the analytical correction term CL−1, solves the problem. The corresponding fit results are collected in table 4. By the same analysis as before, we find ω = 1.540(69) as the best estimate in this case. The optimal minimal lattice size ${L}_{{\rm{\min }}}=64$ appears to be smaller than 128 found for U = U*. It is explained by the fact that the number of fit parameters is increased and, therefore, only fits over a wider range of sizes appear to be reasonably stable.
Table 4. The MC estimates of ω, obtained by fitting the susceptibility data in table 2 to the ansatz χ/L7/4 = A + BL−ω + CL−1 within $L\in [{L}_{{\rm{\min }}},2048]$. The quality of these fits is controlled by the χ2/d.o.f. and the goodness Q values in the last two columns. |
| ${L}_{{\rm{\min }}}$ | ω | χ2/d.o.f. | Q |
|---|---|---|---|
| 24 | 1.269(14) | 3.98 | 1.9 · 10−5 |
| 32 | 1.333(20) | 2.37 | 0.011 |
| 48 | 1.431(40) | 1.61 | 0.117 |
| 64 | 1.540(69) | 1.24 | 0.276 |
Our best MC estimates at U = U* and U = 2 are well consistent. However, there might be some concerns about the possible systematic errors due to the neglect of the constant background contribution, since the exponent − 7/4 in (2 ) is quite close to our actual estimates of − ω. Unfortunately, the inclusion of χ0 as an extra fit parameter does not lead to accurate and stable results because of too many fit parameters. Nevertheless, the possible effect of the background term can be tested by considering fits with several fixed χ0 values within some range of reasonable values. To get an idea about the possible values of χ0, we refer to the known results for the 2D Ising model [32], i.e., χ0 ≈ − 0.1041, χ0 ≈ − 0.0496 and χ0 ≈ − 0.2215 for the ferromagnetic case (β > 0) on square, triangular and honeycomb lattices, respectively, as well as χ0 ≈ 0.1589 and χ0 ≈ 0.1224 for the antiferromagnetic case (β < 0) on square and honeycomb lattices. Recall that the Ising model corresponds to the large-λ limit of the actual φ4 model. Hence, the χ0 value for λ = 10 could be quite close to the Ising value − 0.1041 on the actually considered square lattice. Since the susceptibility χ does not change much with λ (as it can be seen from the plots for λ = 0.1, 1 and 10 in [11]) and χ0 in different cases (referred to above) also are quite similar in magnitude, we do not expect a much larger ∣χ0∣ value in the actual case of λ = 0.1. The exponent ω is changed only very slightly, i.e., from ω = 1.5458(244) to ω = 1.5463(244), if the fit with ${L}_{{\rm{\min }}}=128$ at U = U* is biased by adding the background term with χ0 = − 0.1. The influence on the best fit at U = 2 is slightly larger, showing up as a shift by 0.0011. Thus, the fit at U = U* provides the most accurate and stable value obtained from the susceptibility data if corrections to scaling have the power-law form. We have rounded up its error bars to 0.030 for our final best estimation from the data, i.e., 2 ) if ∣χ0∣ < 1. According to our discussion, it is plausible that ∣χ0∣ is not larger than 1. However, due to the lack of precise information about χ0, the error bars in (4 ) are indicative.
$\begin{eqnarray}\omega =1.546(30)\end{eqnarray}$
to include the statistical error of one standard deviation (σ), as well as the additional uncertainty due to the χ0L−7/4 term in (If the restriction ∣χ0∣ < 1 is removed, the uncertainty in ω becomes significantly larger. In particular, the fit to χ/L7/4 = A + BL−ω + χ0L−7/4 over L ∈ [96, 2048] with fixed ω = 4/3 is relatively good, as we have χ2/d.o.f = 1.32 and Q = 0.236 in this case. It provides some evidence that ω could be consistent with 4/3 reported in [28]. However, an acceptable fit is possible also at a different ω value, e. g., at ω = 1.5. At ω = 4/3, the fitted value of χ0, i.e., χ0 = 26.4(1.6), greatly exceeds in magnitude of the corresponding value χ0 ≈ − 0.1041 of the 2D Ising model. Moreover, in the 2D Ising case, χ0 appears to be always (for all lattices considered in [32]) negative for the ferromagnetic interaction and positive for the antiferromagnetic one. Since we have the ferromagnetic interaction, the positive value of χ0 = 26.4(1.6) does not fit in this qualitative picture. Hence, the validity of the fit with ω = 4/3 seems doubtful from an intuitive point of view, at least. Another aspect is that the estimate (4 ) agrees well with several other estimates, summarized in section 3.4 , obtained under the assumption of a pure power-law scaling of the correction terms. This agreement with (4 ) and disagreement with ω = 4/3 of all these estimates could not be accidental. Hence, if we have the pure power-law scaling form, then ω is about 1.546 rather than 4/3. Finally, although the estimated error bars are never rigorous due to the possible influence of the correction terms not included in the fit ansatz, the good consistency of the results serves as reasonable evidence that these error bars are not essentially underestimated.
The estimated value of ω changes if we include logarithmic corrections. In particular, our best estimate ω = 1.546(24) in table 3 changes to 1.348(25) (with χ2/d.o.f. = 1.32 and Q = 0.243) for the $1/\mathrm{ln}L$ logarithmic correction (κ = − 1), and to 1.744(24) (with χ2/d.o.f. = 1.38 and Q = 0.218) for the $\mathrm{ln}L$ logarithmic correction (κ = 1). Thus, the data appears to be consistent with ω = 4/3 in the first case and with ω = 7/4 in the second case. We note that the first value might be expected according to the results of [28] discussed in section 1 , whereas the second value agrees well with the result ω = 1.71(10) of the ε-expansion in [7], where 1.75 has been considered as the exact value.
Despite this variation in ω depending on κ in the fit ansatz (3 ), the uncertainty in ω is quite small for our estimation procedure at a fixed κ = 0 and U = U*, assuming a small influence of the χ0L−7/4 term in agreement with the arguments provided before. It is manifested in (4 ) and can be concluded also from the χ/L7/4 versus aL−ω plots (where a is a scaling factor, different for each ω) at ω = 4/3, 1.546 and 7/4 shown in figure 1 for the range of sizes L ∈ [64, 2048].
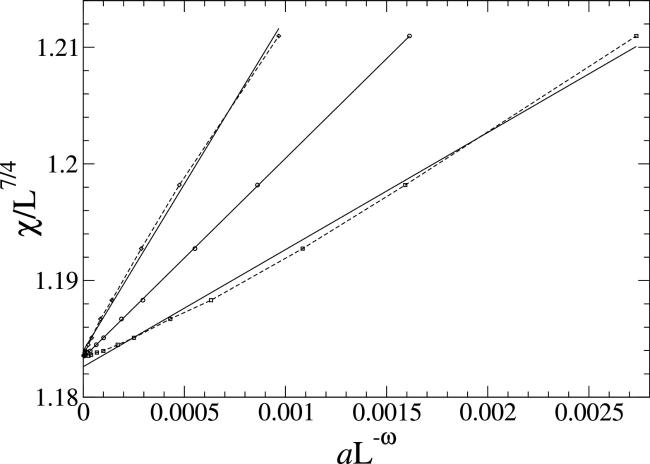
Figure 1. The χ/L7/4 versus aL−ω plots within L ∈ [64, 2048] for U = U* at a = 0.7, ω = 4/3 (squares); a = 1, ω = 1.546 (circles); and a = 1.4, ω = 7/4 (diamonds). The statistical errors of one σ are smaller than the symbol size. The linear fits are shown by straight lines. |
The χ/L7/4 versus aL−ω plot is almost perfectly linear at ω = 1.546 and is essentially curved at ω = 4/3. It indicates that the uncertainty in the estimation of ω at fixed κ = 0 is essentially smaller than the difference between 1.546 and 4/3.
Since the logarithmic corrections can be expected at ω = 4/3, we have presented the plots for χ/L7/4 versus $a{L}^{-4/3}{(\mathrm{ln}L)}^{\kappa }$ with κ = ± 1 in figure 2.
Figure 2. The χ/L7/4 versus $a{L}^{-4/3}{(\mathrm{ln}L)}^{\kappa }$ plots within L ∈ [64, 2048] for U = U* at a = 1, κ = − 1 (squares) and a = 0.1, κ = 1 (triangles). The statistical errors of one σ are smaller than the symbol size. The linear fits are shown by straight lines. |
It is evident from this figure that the $\propto {L}^{-4/3}\mathrm{ln}L$ scaling (κ = 1) is even worse in consistency with the data than the ∝ L−4/3 scaling tested in figure 1. On the contrary, the plot with κ = − 1 in figure 2 looks almost perfectly linear. The χ2/d.o.f. values of the corresponding linear fits within $L\in [{L}_{{\rm{\min }}},2048]$ are 1.89, 1.82 and 1.18 for ${L}_{{\rm{\min }}}=64,96$ and 128, respectively. The corresponding Q values are 0.049, 0.069 and 0.31. It means that the fit within L ∈ [128, 2048] is well acceptable (even slightly better than the fit with the L−ω correction) and the $\propto {L}^{-4/3}/\mathrm{ln}L$ correction-to-scaling behavior is consistent with our data for L≥128 at U = U*. The consistency at U = 2 has also been verified. The fit of this data to the ansatz $\chi /{L}^{7/4}=A+B{L}^{-4/3}\,{(\mathrm{ln}L)}^{-1}+C{L}^{-1}$ within L ∈ [64, 2048] with χ2/d.o.f. = 1.30 and Q = 0.24 is almost as good as the corresponding fit to the ansatz χ/L7/4 = A + BL−ω + CL−1 (see table 4). One can also fit the same data set to $\chi /{L}^{7/4}=A+B{L}^{-7/4}\,\mathrm{ln}L+C{L}^{-1}$ with χ2/d.o.f. = 1.33 and Q = 0.225.
3.2. Estimation from the ∂U/∂β data
Similar scaling arguments as in section 3.1 can be applied also to the derivative ∂U/∂β with the only difference being that the additive constant analytical background contribution is not expected in this case, since ∂U/∂β is strictly zero in the thermodynamic limit at β ≠ βc. It is confirmed by the fits of our − (∂U/∂β)/L data for U = U*. The additive background term would give a ~ L−1 correction, which is not observed in this case. Such a correction appears at U ≠ U* as a multiplicative analytical correction. Hence, neglecting corrections of higher orders, − (∂U/∂β)/L at $\beta ={\widetilde{\beta }}_{c}(L)$ can be approximated by
$\begin{eqnarray}-(\partial U/\partial \beta )/L=A+B{L}^{-\omega }+C{L}^{-1},\end{eqnarray}$
with C = 0 for U = U*. In the case of the logarithmic corrections, this ansatz has to be modified as $\begin{eqnarray}-(\partial U/\partial \beta )/L=A+B{L}^{-\omega }\,{(\mathrm{ln}L)}^{\kappa }+C{L}^{-1}\ .\end{eqnarray}$
First, we test the pure power-law scaling using (5 ). Thus, for U = U*, a simple ansatz − (∂U/∂β)/L = A + BL−ω is applicable in this case, and the corresponding fit results are shown in table 5. The obtained values of ω, however, are varied remarkably with the minimal lattice size ${L}_{{\rm{\min }}}$ used in the fits. The results are stabilized, including the expected next correction ∝ L−2. Such fits have already been considered in [11], providing ω = 1.373(48) by fitting over the range L ∈ [12, 1536] with χ2/d.o.f = 1.5 and Q = 0.123. The poor and marginal quality of those fits in [11] raised doubts about the validity of the ansatz used. This situation is improved essentially by the actual refined data in table 1. The fit at ${L}_{{\rm{\min }}}=12$ is poor and gives a similar ω value than the one reported in [11]. However, we obtain moderately good and consistent fits for ${L}_{{\rm{\min }}}=24$ and ${L}_{{\rm{\min }}}=32$, as shown in table 6. Hence, we report ω = 1.567(58) as the best estimate from the ∂U/∂β data with U = U*, if the non-analytical corrections to scaling have the pure power-law form, because the results of this fitting procedure are reasonably stable and the corresponding fit in table 6 at ${L}_{{\rm{\min }}}=24$ is well acceptable and has the highest quality according to the χ2/d.o.f and Q criteria.
Table 5. The MC estimates of ω, obtained by fitting the ∂U/∂β data in table 1 to the ansatz − (∂U/∂β)/L = A + BL−ω within $L\in [{L}_{{\rm{\min }}},2048]$. The quality of these fits is controlled by the χ2/d.o.f. and the goodness Q values in the last two columns. |
| ${L}_{{\rm{\min }}}$ | ω | χ2/d.o.f. | Q |
|---|---|---|---|
| 24 | 1.1747(95) | 5.96 | 8.3 · 10−10 |
| 32 | 1.246(15) | 2.41 | 0.0074 |
| 48 | 1.318(29) | 1.76 | 0.070 |
| 64 | 1.393(47) | 1.44 | 0.175 |
| 96 | 1.512(96) | 1.35 | 0.220 |
| 128 | 1.81(19) | 0.77 | 0.591 |
Table 6. The MC estimates of ω, obtained by fitting the ∂U/∂β data in table 1 to the ansatz − (∂U/∂β)/L = A + BL−ω + CL−2 within $L\in [{L}_{{\rm{\min }}},2048]$. The quality of these fits is controlled by the χ2/d.o.f. and the goodness Q values in the last two columns. |
| ${L}_{{\rm{\min }}}$ | ω | χ2/d.o.f. | Q |
|---|---|---|---|
| 8 | 1.2965(84) | 5.85 | 6.1 · 10−11 |
| 12 | 1.398(16) | 1.70 | 0.060 |
| 16 | 1.434(28) | 1.76 | 0.084 |
| 24 | 1.567(58) | 1.07 | 0.383 |
| 32 | 1.59(10) | 1.18 | 0.304 |
We have performed fits of the − (∂U/∂β)/L data for U = 2 in table 2, starting with a simple ansatz − (∂U/∂β)/L = A + BL−ω to compare the results with those in [11]. Such fits over L ∈ [16, 1536] in [11] provided an evidence that ω, probably, is 1/2. Having extended and more accurate actual data, we have tested how the results change for significantly larger than 16 values of ${L}_{{\rm{\min }}}$, as shown in table 7. It can be seen that ω about 1/2 describes a transient behavior, since the estimated value of ω tends to increase with ${L}_{{\rm{\min }}}$, perhaps, to the value ω = 1, provided by the analytical correction term ~ L−1. In this case, one needs to include this correction term into the ansatz to extract the non-analytical correction exponent, if it exists. Hence, we have used the ansatz (5 ) in the second round of fitting these data. Although the corresponding fit results in table 8 are not very accurate and stable, the best estimate of this kind, i.e., ω = 1.61(44) at ${L}_{{\rm{\min }}}=64$, appears to be consistent with our other best estimates at the assumption of pure power-law scaling.
Table 7. The MC estimates of ω, obtained by fitting the ∂U/∂β data in table 2 to the ansatz − (∂U/∂β)/L = A + BL−ω within $L\in [{L}_{{\rm{\min }}},2048]$. The quality of these fits is controlled by the χ2/d.o.f. and the goodness Q values in the last two columns. |
| ${L}_{{\rm{\min }}}$ | ω | χ2/d.o.f. | Q |
|---|---|---|---|
| 16 | 0.4472(87) | 7.52 | 4.4 · 10−14 |
| 24 | 0.497(12) | 5.27 | 2.2 · 10−8 |
| 32 | 0.553(17) | 3.17 | 0.00045 |
| 48 | 0.629(26) | 1.61 | 0.105 |
| 64 | 0.621(33) | 1.80 | 0.072 |
| 96 | 0.715(54) | 1.32 | 0.234 |
| 128 | 0.850(85) | 0.69 | 0.657 |
Table 8. The MC estimates of ω, obtained by fitting the ∂U/∂β data in table 2 to the ansatz − (∂U/∂β)/L = A + BL−ω + CL−1 within $L\in [{L}_{{\rm{\min }}},2048]$. The quality of these fits is controlled by the χ2/d.o.f. and the goodness Q values in the last two columns. |
| ${L}_{{\rm{\min }}}$ | ω | χ2/d.o.f. | Q |
|---|---|---|---|
| 8 | 0.533(21) | 6.91 | 1.5 · 10−13 |
| 12 | 0.729(35) | 2.55 | 0.0022 |
| 16 | 0.819(49) | 2.11 | 0.017 |
| 24 | 1.039(93) | 1.37 | 0.186 |
| 32 | 1.08(14) | 1.51 | 0.139 |
| 48 | 0.92(21) | 1.61 | 0.117 |
| 64 | 1.61(44) | 1.05 | 0.392 |
Allowing for the logarithmic corrections, we have verified the consistency of the data at U = U* with the $\propto {L}^{-4/3}/\mathrm{ln}L$ corrections to scaling. We have tested the quality of the fit in the case that L−ω is replaced by ${L}^{-4/3}/\mathrm{ln}L$ in our best power-law estimation, presented in table 6. In this case, we have χ2/d.o.f. = 1.56 and Q = 0.103 for the fit within L ∈ [24, 2048]. This fit appears to be somewhat worse than the corresponding fit with Q = 0.383 in table 4, but it is still acceptable. It is interesting to mention that the fit with the $\propto {L}^{-7/4}\mathrm{ln}L$ correction (as one of the options following from the analysis in section 3.1 ) is relatively good in this case, i.e., it has χ2/d.o.f. = 1.03 and Q = 0.417.
The fits to (6 ) with ω = 4/3 and κ = − 1, as well as with ω = 7/4 and κ = 1 are relatively good at U = 2. Namely, for the fits over L ∈ [64, 2048], we have χ2/d.o.f. = 0.92, Q = 0.496 in the first case and χ2/d.o.f. = 0.94, Q = 0.482 in the second case, which can be compared with the corresponding values in table 8.
3.3. Estimation from the pseudocritical couplings
It is also possible to estimate ω from the scaling of the pseudocritical couplings ${\widetilde{\beta }}_{c}(L)$. As mentioned in section 3.1 , their scaling is asymptotically consistent with U = F(tL1/ν). Corrections to scaling have to be included here for the estimation of ω, i.e., 7 ) and (8 ) at a fixed U. Recalling that ${\widetilde{\beta }}_{c}(L)-{\beta }_{c}\propto t(L)$, we find from these equations ${\widetilde{\beta }}_{c}(L)-{\beta }_{c}\unicode{x0007E}{L}^{-\frac{1}{\nu }-\omega }$ at U = U*, provided that $\frac{1}{\nu }+\omega \lt 2\omega $ holds, which is obviously true in our 2D case. At U ≠ U*, there are also two additional terms ${ \mathcal O }\left({L}^{-1/\nu }\right)$ and ${ \mathcal O }\left({L}^{-2/\nu }\right)$, which reduce to the ∝ L−1 and ∝ L−2 corrections in our 2D case. It makes the estimation of ω very challenging. Therefore, we focus only on the U = U* case, using the ansatz
$\begin{eqnarray}U=F\left(\left(t+{ \mathcal O }\left({t}^{2}\right)\right){L}^{1/\nu }\right)+{ \mathcal O }\left({L}^{-\omega }\right),\end{eqnarray}$
where analytical corrections to scaling are included via the ${ \mathcal O }\left({t}^{2}\right)$ term, whereas the ${ \mathcal O }\left({L}^{-\omega }\right)$ term represents the non-analytical correction. The scaling function F(z) is regular at z = 0, so that it can be expanded in powers of z, i.e., $\begin{eqnarray}F(z)=F(0)+z\,F^{\prime} (0)+\frac{1}{2}{z}^{2}\,F^{\prime\prime} (0)+\cdots ,\end{eqnarray}$
noting that F(0) = U* holds. We can calculate t as a function of L from ( $\begin{eqnarray}{\widetilde{\beta }}_{c}(L)={\beta }_{c}+A\,{L}^{-1-\omega }\,{(\mathrm{ln}L)}^{\kappa },\end{eqnarray}$
for testing of the pure power-law scenario with κ = 0 and allowing also for logarithmic corrections.The fitting results over $L\in [{L}_{{\rm{\min }}},2048]$ at κ = 0 are presented in table 9. The quality of these fits is acceptable for ${L}_{{\rm{\min }}}\geqslant 48$. Formally, the fit with ${L}_{{\rm{\min }}}=48$ is the best one, yielding ω = 1.5019(91). However, this value is the smallest one among those ones provided by the set of acceptable fits in table 9. Noting that there might be a small systematic shift of the estimated ω value with increasing ${L}_{{\rm{\min }}}$ (masked, however, by statistical errors), we have chosen ω = 1.509(14), obtained at ${L}_{{\rm{\min }}}=64$, as our final best estimate from this data set. This is motivated by the fact that this fit is almost as good as the one at ${L}_{{\rm{\min }}}=48$. Still, the error bars are slightly larger (which increases the chance that the estimated ω value is correct within the stated error bars). The value of ω agrees well with the other acceptable values in table 9, as well as with all the other best estimates in our paper made at the assumption of the pure power-law scaling.
Table 9. The MC estimates of ω, obtained by fitting the pseudocritical couplings in table 1 to the ansatz ${\widetilde{\beta }}_{c}(L)={\beta }_{c}+A\,{L}^{-1-\omega }$ within $L\in [{L}_{{\rm{\min }}},2048]$. The quality of these fits is controlled by the χ2/d.o.f. and the goodness Q values in the last two columns. |
| ${L}_{{\rm{\min }}}$ | ω | χ2/d.o.f. | Q |
|---|---|---|---|
| 32 | 1.4501(48) | 5.99 | 3.7 · 10−9 |
| 48 | 1.5019(91) | 1.28 | 0.243 |
| 64 | 1.509(14) | 1.38 | 0.198 |
| 96 | 1.531(29) | 1.47 | 0.172 |
| 128 | 1.511(46) | 1.67 | 0.124 |
We have also tested the consistency with ω = 4/3. Just as in the case with the susceptibility data at U = U*, no consistency is observed at κ = 0 and κ = 1 in (9 ), assuming ω = 4/3, but the data can be fit reasonably well with κ = − 1 in this case. The fit results are collected in table 10. Compared with the results in table 9, we can see that the quality of the fits in table 10 is significantly lower for ${L}_{{\rm{\min }}}=48$ and ${L}_{{\rm{\min }}}=64$. However, it is even higher for ${L}_{{\rm{\min }}}=96$ and ${L}_{{\rm{\min }}}=128$.
Table 10. The χ2/d.o.f. and Q values for the fits of the pseudocritical couplings in table 1 to the ansatz ${\widetilde{\beta }}_{c}(L)={\beta }_{c}+A\,{L}^{-7/3}/\mathrm{ln}L$ within $L\in [{L}_{{\rm{\min }}},2048]$. |
| ${L}_{{\rm{\min }}}$ | χ2/d.o.f. | Q |
|---|---|---|
| 48 | 5.98 | 4 · 10−9 |
| 64 | 2.28 | 0.015 |
| 96 | 1.23 | 0.279 |
| 128 | 1.40 | 0.200 |
We have shown and compared the pure power-law fits with ω = 1.509 and ω = 4/3, as well as the fit with ω = 4/3 and κ = − 1 over L ∈ [48, 2048] and L ∈ [96, 2048] in figure 3. In the case of L ∈ [48, 2048], a slight curvature of the ${\widetilde{\beta }}_{c}(L)$ versus the ${L}^{-7/3}/\mathrm{ln}L$ data curve (dashed line) can be seen, compared with the corresponding liner fit. It is in favor of the pure power-law dependence with ω = 1.509. However, the linear fit to (9 ) with ω = 4/3 and κ = − 1 looks perfect within L ∈ [96, 2048] and even better than the power-law fit with ω = 1.509. Thus, (9 ) with ω = 4/3 and κ = − 1 can be the correct asymptotic ansatz. At the same time, the pure power-law fits with ω = 4/3 are not good, as the ${\widetilde{\beta }}_{c}$ versus 0.75L−7/3 plots show a remarkable curvature. These fits are not acceptable according to the formal criteria: χ2/d.o.f = 39.65, Q = 5.3 · 10−79 for L ∈ [48, 2048] and χ2/d.o.f = 7.88, Q = 1.2 · 10−10 for L ∈ [96, 2048].
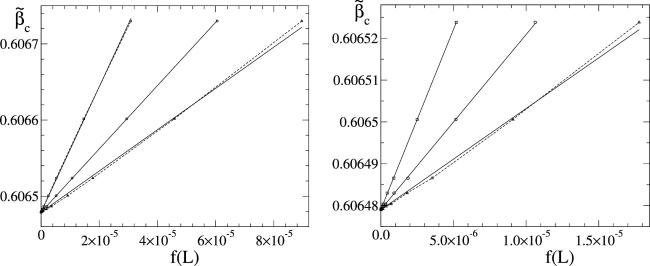
Figure 3. The ${\widetilde{\beta }}_{c}$ vs the f(L) plots at U = U* within L ∈ [48, 2048] (left) and L ∈ [96, 2048] (right) for f(L) = L−2.509 (circles), $f(L)={L}^{-7/3}/\mathrm{ln}L$ (squares) and f(L) = 0.75L−7/3 (triangles). The statistical errors of one σ are smaller than the symbol size in the left picture. These are about the same symbol size or smaller in the right picture. The linear fits are shown by solid straight lines. |
Finally, we would like to mention that the fits with ω = 7/4 and κ = 1 are acceptable. In this case, we have χ2/d.o.f. = 1.51, Q = 0.128 and χ2/d.o.f. = 1.42, Q = 0.180 for the fits over L ∈ [48, 2048] and L ∈ [96, 2048], respectively.
3.4. Summary of the MC estimations and comparison
In summary of our MC estimation, we have found a set of estimates for the correction-to-scaling exponent ω, which are valid if the corrections to scaling have a pure power-law form. The most accurate of them are ω = 1.509(14) and ω = 1.546(30) obtained from our MC data of the pseudocritical couplings and susceptibility, respectively, for U = U* listed in table 1. Three other estimates of this set are ω = 1.540(69), obtained from the susceptibility data at U = 2 (table 2), as well as ω = 1.567(58) and ω = 1.61(44), obtained from the ∂U/∂β data at U = U* and U = 2, respectively. All these values are consistent within the error bars. These estimates agree well with the result ω = 1.6(2) of the ε-expansion reported in [34], but are not as consistent with the more recent result of this expansion ω = 1.71(10) in [7].
Allowing for logarithmic corrections, our data appears to be consistent with ω = 4/3, if the leading non-analytical correction to scaling is modified by the logarithmic factor of the form $1/\mathrm{ln}L$, and with ω = 7/4, if this logarithmic factor is just $\mathrm{ln}L$. In the first case, the exponent ω is such one, which can be expected from the results of [28], noting that some logarithmic correction could be, indeed, expected in this case—see section 1 . In the second case, the value of ω agrees well with 1.71(10) obtained from the ε-expansion in [7]. There is only a question about the existence of the logarithmic correction in this case.
Here, the refined estimations do not confirm the existence of corrections to scaling with the full set of exponents n/4, discussed in [11], where n is an integer number, although it confirms the existence of non-integer exponents suggested earlier [11]. Note that only the integer correction exponents are usually expected in the 2D Ising model, where ω = 2 [25]. It corresponds to the limit λ → ∞. In our previous study [11], we have considered λ = 0.1, 1, 10, noting that the λ = 0.1 case gives a better chance to identify corrections with non-integer ω. Here we have focused just on this case. There might be a danger that the convergence to the correct asymptotic exponents becomes slower with decreasing λ, since λ = 0 corresponds to the free-field or Gaussian model. However, the normalized quantities χ/L7/4 and (∂U/∂β)/L show the expected convergence to constant values, showing that the asymptotic scaling regime is reached in our simulations at λ = 0.1. In fact, ω = 2 is expected from the conformal field theory (CFT) [25] in the 2D φ4 model, just as in the 2D Ising model, so that the non-integer values of ω provided by our fits requires further examination from the point of view of the CFT. Perhaps, one should allow that the CFT does not entirely describe all corrections to scaling. Such a possibility has been discussed in [33].
4. The singularity of specific heat and the two-point correlation function
In [11], theoretical arguments have been provided concerning corrections to scaling in the two-point correlation function, based on the continuous version of the φ4 model with 11 ), keeping a finite number of terms, where gi(kξ) are continuous scaling functions, which are finite for 0 ≤ kξ < ∞. Here, θ0 = 0 holds and the term with i = 0 describes the leading singularity, whereas the terms with i ≥ 1 represent other contributions with correction exponents θi > 0. The critical correlation function
$\begin{eqnarray}\frac{{ \mathcal H }}{{k}_{{\rm{B}}}T}=\int \left({r}_{0}{\varphi }^{2}(x)+c{({\rm{\nabla }}\varphi ({\boldsymbol{x}}))}^{2}+u{\varphi }^{4}({\boldsymbol{x}})\right){\rm{d}}{\boldsymbol{x}},\end{eqnarray}$
where the order parameter φ(x) is an N-component vector with components φi(x) depending on the coordinate x. It is assumed that there exists the upper cut-off parameter Λ for the Fourier components of the order-parameter field φi(x). It is assumed that r0 is the linear function of T, c and u being constants. In this case, the singular part of specific heat CV can be written as [11] $\begin{eqnarray}{C}_{V}^{{\rm{sing}}}\propto {\xi }^{1/\nu }\,{\left({\int }_{k\lt {\rm{\Lambda }}}[G({\boldsymbol{k}})-{G}^{* }({\boldsymbol{k}})]{\rm{d}}{\boldsymbol{k}}\right)}^{{\rm{sing}}},\end{eqnarray}$
where k = ∣k∣, ξ is the correlation length, and G(k) is the Fourier-transformed two-point correlation function having the value G*(k) at the critical point. The scaling hypothesis in the form of $\begin{eqnarray}G({\boldsymbol{k}})=\displaystyle \sum _{i\geqslant 0}{\xi }^{(\gamma -{\theta }_{i})/\nu }{g}_{i}(k\xi ),\end{eqnarray}$
has been applied for the calculation of ( $\begin{eqnarray}{G}^{* }({\boldsymbol{k}})=\displaystyle \sum _{i\geqslant 0}{b}_{i}{k}^{(-\gamma +{\theta }_{i})/\nu }\end{eqnarray}$
is obtained at ξ → ∞, so that there exists a finite limit $\begin{eqnarray}\mathop{\mathrm{lim}}\limits_{z\to \infty }{z}^{(\gamma -{\theta }_{i})/\nu }{g}_{i}(z)={b}_{i},\end{eqnarray}$
where bi are constant coefficients.An additional assumption has been made, according to which the correct leading singularity of CV with a certain constant amplitude is provided by the integration over the region $k\lt {\rm{\Lambda }}^{\prime} $ in (11 ) in the limit $\mathop{\mathrm{lim}}\limits_{{\rm{\Lambda }}^{\prime} \to 0}\mathop{\mathrm{lim}}\limits_{\xi \to \infty }$. It implies that this small k contribution is asymptotically (at ξ → ∞) independent of ${\rm{\Lambda }}^{\prime} $ for small enough values of ${\rm{\Lambda }}^{\prime} $. In other words, we can separate a certain ${\rm{\Lambda }}^{\prime} $-independent long-wavelength contribution.
A theorem has been proven in [11], according to which the known logarithmic singularity of CV at d = 2 is possible only if there exists a correction with the exponent ωi = θi/ν = 3/4 at the assumptions made. This exponent, however, is not confirmed by our current MC estimation. It raises the question: what could be wrong with these assumptions or conditions of the theorem? Some numerical tests have been performed in [11] to verify these assumptions. In particular, it has been checked that (11 ) really provides the logarithmic singularity of the form ${C}_{V}=C\mathrm{ln}\xi $, where C is a constant. Moreover, it has been checked that the logarithmic singularity is provided separately by the contributions of $0\lt k\lt {\rm{\Lambda }}^{\prime} $ and ${\rm{\Lambda }}^{\prime} \lt k\lt {\rm{\Lambda }}$ for certain finite values of ${\rm{\Lambda }}^{\prime} $. According to the assumptions made, these contributions, denoted as $A({\rm{\Lambda }}^{\prime} )\mathrm{ln}\xi $ and $B({\rm{\Lambda }}^{\prime} )\mathrm{ln}\xi $ with $A({\rm{\Lambda }}^{\prime} )+B({\rm{\Lambda }}^{\prime} )=C$, should be almost independent of ${\rm{\Lambda }}^{\prime} $ for small enough values of ${\rm{\Lambda }}^{\prime} $. The dependence of $A({\rm{\Lambda }}^{\prime} )$ and $B({\rm{\Lambda }}^{\prime} )$ has not really been tested for small ${\rm{\Lambda }}^{\prime} $ values, relying on the intuitive assumption that $A({\rm{\Lambda }}^{\prime} )\mathrm{ln}\xi $ has to be asymptotically ${\rm{\Lambda }}^{\prime} $-independent at small ${\rm{\Lambda }}^{\prime} $ and $\xi {\rm{\Lambda }}^{\prime} \to \infty $ as a long-wavelength contribution, where only vanishing small wave vectors are relevant at $\xi {\rm{\Lambda }}^{\prime} \to \infty $.
As we currently do not see a reason why the scaling relations (12 )–(14 ) could not be valid for the estimation of the leading long-wavelength contribution, we propose that the reason for the discrepancy with the MC estimation of ω is that $A({\rm{\Lambda }}^{\prime} )$ essentially depends on ${\rm{\Lambda }}^{\prime} $ for small ${\rm{\Lambda }}^{\prime} $ contrary to the assumption made in [11]. From a formal point of view, it is even very likely that $-B({\rm{\Lambda }}^{\prime} )$ and $A({\rm{\Lambda }}^{\prime} )$ diverge at ${\rm{\Lambda }}^{\prime} \to 0$ according to the scaling behavior shown in figure 6 of [11], where ∣k∂G(k)/∂β∣ tends to increase rapidly for small k in the vicinity of the critical point (at t = 0.005). This also allows us to relate the leading logarithmic singularity of CV to the leading singularity of G(k), rather than to correction terms, which is quite plausible from an intuitive point of view.
Keeping only the leading term in (13 ) and (14 ), we have 15 ) into (11 ), where we formally set ${\rm{\Lambda }}\to {\rm{\Lambda }}^{\prime} $ for the estimation of the long-wavelength contribution ${C}_{V}^{{\rm{sing}}}({\rm{\Lambda }}^{\prime} )$, we obtain
$\begin{eqnarray}G({\boldsymbol{k}})-{G}^{* }({\boldsymbol{k}})\approx {\xi }^{\lambda }\tilde{g}(k\xi )\,,\end{eqnarray}$
where λ = γ/ν = 2 − η, η being the critical exponent describing the behavior of the critical correlation function, i.e., G*(k) ≈ b0k−λ = b0k−2+η at k → 0, and $\begin{eqnarray}\tilde{g}(k\xi )=g(k\xi )-{b}_{0}{(k\xi )}^{-\lambda }\,.\end{eqnarray}$
Inserting ( $\begin{eqnarray}\begin{array}{rcl}{C}_{V}^{{\rm{sing}}}({\rm{\Lambda }}^{\prime} ) & \propto & {\xi }^{\frac{1}{\nu }+\lambda }\underset{0}{\overset{{\rm{\Lambda }}^{\prime} }{\displaystyle \int }}\tilde{g}(k\xi ){k}^{d-1}{\rm{d}}k\\ & = & {\xi }^{\frac{1}{\nu }+\lambda -d}\underset{0}{\overset{\xi {\rm{\Lambda }}^{\prime} }{\displaystyle \int }}\tilde{g}(z){z}^{d-1}{\rm{d}}z={\xi }^{\frac{1}{\nu }+\lambda -d}\,F(\xi {\rm{\Lambda }}^{\prime} )\,,\end{array}\end{eqnarray}$
where $F(\xi {\rm{\Lambda }}^{\prime} )$ is some function of the given argument.According to the arguments in [11], $F(\xi {\rm{\Lambda }}^{\prime} )$ should be independent of ${\rm{\Lambda }}^{\prime} $ in the limit $\mathop{\mathrm{lim}}\limits_{{\rm{\Lambda }}^{\prime} \to 0}\mathop{\mathrm{lim}}\limits_{\xi \to \infty }$, if (17 ) represents the leading singularity of CV. It is possible, e.g., if F(z) tends to some nonzero constant at z → ∞. However, then we obtain ${C}_{V}^{{\rm{sing}}}\propto {\xi }^{3/4}$ in two dimensions instead of the expected logarithmic singularity. No ${\rm{\Lambda }}^{\prime} $-independent logarithmic singularity can be obtained from (17 ) at d = 2. Therefore, the formal conclusion from the considerations in [11] was that $F(\xi {\rm{\Lambda }}^{\prime} )$ vanishes at $\xi {\rm{\Lambda }}^{\prime} \to \infty $ in such a way that ${\xi }^{\frac{1}{\nu }+\lambda -d}\,F(\xi {\rm{\Lambda }}^{\prime} )$ does not represent the leading singularity of CV, the latter being provided by a correction-to-scaling term.
Here we consider another possibility, allowing that (17 ) represents the leading singularity of CV with ${\rm{\Lambda }}^{\prime} $-dependent amplitude. This approximation is applicable at $\xi {\rm{\Lambda }}^{\prime} \to \infty $ for any given ${\rm{\Lambda }}^{\prime} $, which should be small enough to ensure the validity of (17 ). We have $\frac{1}{\nu }+\lambda -d=3/4$ at d = 2, so that the expected logarithmic singularity is recovered if $F(z)\propto {z}^{-3/4}\mathrm{ln}z$ holds at z → ∞. It implies that ${C}_{V}^{{\rm{sing}}}({\rm{\Lambda }}^{\prime} )$ is proportional to ${({\rm{\Lambda }}^{\prime} )}^{-3/4}$ at ξ → ∞. To show that this new possibility is physically meaningful, we point to the fact that ${\xi }^{\frac{1}{\nu }+\lambda -d}\,F(\xi {\rm{\Lambda }}^{\prime} )$ can be seen as a long-wavelength contribution according to some criterion.
The old criterion in [11] states that the long-wavelength contribution is such one, which is independent of ${\rm{\Lambda }}^{\prime} $. The actual new criterion states that a long-wavelength contribution is such one, for which a small k subregion $0\lt k\lt { \mathcal C }/\xi $ is relevant at ξ → ∞ for any positive constant ${ \mathcal C }$. In other words, this contribution has to be changed significantly, if this subregion is cut off. Such a cutting procedure essentially modifies the result (17 ) from ${\xi }^{\frac{1}{\nu }+\lambda -d}F(\xi {\rm{\Lambda }}^{\prime} )$ to ${\xi }^{\frac{1}{\nu }+\lambda -d}(f({ \mathcal C })+F(\xi {\rm{\Lambda }}^{\prime} ))$, where $f({ \mathcal C })$ is a function of ${ \mathcal C }$. Hence, (17 ) can be seen as a long-wavelength contribution according to the new criterion proposed.
The new criterion can be seen as a generalization of the old one. Indeed, if we deal with contributions, which just come from the region k ~ 1/ξ and are independent of ${\rm{\Lambda }}^{\prime} $, then these contributions are modified by the cutting of a subregion of k ~ 1/ξ. Hence, these are the long-wavelength contributions according to both criteria. A relevant example is ${C}_{V}^{{\rm{sing}}}({\rm{\Lambda }}^{\prime} )$ above the upper critical dimension, i.e., at d > 4. In this case, the correct leading singularity ${C}_{V}^{{\rm{sing}}}\propto {\xi }^{4-d}\propto \,| t{| }^{(d-4)/2}$ is recovered at a constant (nonzero) asymptotic value of F(z) at z → ∞. The quantity ${C}_{V}^{{\rm{sing}}}({\rm{\Lambda }}^{\prime} )$ appears to be ${\rm{\Lambda }}^{\prime} $-independent in this case.
Summarizing the discussion of this section, we have proposed here a new scaling conception for the calculation of the leading singularity of CV in the actually considered continuous φ4 model. It is based on a more flexible scaling assumption concerning the behavior of the function $F(\xi {\rm{\Lambda }}^{\prime} )$ in (17 ), as compared to the earlier consideration in [11]. Namely, here we allow that F(z) essentially depends on z at z → ∞, showing that (17 ) can still be seen as a physically meaningful long-wavelength contribution in this case. It shows how the correct leading singularity of CV can be obtained without any conditions for the correction-to-scaling exponents. Hence, no correction exponent 3/4 is expected from the actual consideration at d = 2. It resolves the apparent contradiction between the theory and the MC estimation due to the earlier assumptions in [11].
5. A renewed analysis by grouping of the Feynman diagrams
A method of grouping Feynman diagrams (GFD) has been proposed in [6] for the analysis of critical exponents in the φ4 model. Later on [35], this method has been extended to the analysis of the Goldstone mode singularity. The analysis in these papers refers basically to the case d < 4, and all considerations in this section also refer to this case.
The analysis in [6] requires a significant reconsideration from the point of view of the actual MC results in section 3 and findings in section 4 . The grouping of the Feynman diagrams in [6] has been done in a formally rigorous way. Only the analysis of the resulting equations is somewhat problematic.
The analysis at T → Tc, leading to a certain prediction for the possible values of the critical exponents γ and ν [6], is largely based on the old, rather than the new scaling assumption concerning the relevant long-wavelength contribution to specific heat CV, discussed in section 4 . The new scaling conception is more flexible and, therefore, it does not lead to restrictions for the possible values of the critical exponents. Hence, the prediction for γ and ν in [6] is not further supported by the renewed analysis.
The method of analysis of the two-point correlation function G(k) at the critical point in [6] could be meaningful, in regards to the leading asymptotic behavior, at least. The equation for G(k) at T = Tc has the form 18 ) contains also a nonperturbative correction term, which is neglected in the limit of small u and small k considered throughout that paper. The quantity R(k) is evaluated at G(k) in the form of (13 ), resulting in
$\begin{eqnarray}\frac{1}{2G({\boldsymbol{k}})}=R({\boldsymbol{k}})-R({\boldsymbol{0}})+c{k}^{2},\end{eqnarray}$
where R(k) is represented by a resummed sum of the many so-called skeleton diagrams in [6]. In the formal analysis of [6], equation ( $\begin{eqnarray}R({\boldsymbol{k}})-R({\boldsymbol{0}})=\displaystyle \sum _{i\geqslant 0}{k}^{\lambda +{\omega }_{i}}\,{{\rm{\Psi }}}_{i}({\rm{\Lambda }}/k),\end{eqnarray}$
where ωi = θi/ν and $\Psi$i(Λ/k) are scaling functions, which depend on Λ/k, as well as on other arguments (d, N, λ, ωi and u), which are skipped here for brevity. According to the assumption in [6], these scaling functions can be approximated by Λ-independent constants at small k. It is justified if the relevant long-wavelength contributions come from the region qℓ ~ k, where qℓ denotes the ℓ-th internal wave vector contained in the diagrams of R(k).If only the leading term is taken into account, then (19 ) contains only one scaling function $\Psi$0(Λ/k). It is expected that $\Psi$0(Λ/k) tends to a certain finite positive value at Λ/k → ∞ to ensure that (18 ) has a positively defined solution in the form of G(k) ∝ k−λ at k → 0 with λ < 2. However, the applicability of this analysis cannot be rigorously proven, as we cannot really sum up all the diagrams and are aware that $\Psi$0(Λ/k) does indeed tend to a finite positive value. Alternatively, one can formally set ${\rm{\Lambda }}={ \mathcal C }k$ or ${\rm{\Lambda }}/k={ \mathcal C }$, where ${ \mathcal C }$ is a finite positive constant, considering this as some approximation.
If corrections to scaling are taken into account, then at least one of the terms R(k) − R(0) and 1/(2G(k)) contains a correction with the exponent ω1 = 2 − λ = η to compensate the term ck2 in (18 ). At the assumption that $\Psi$i(Λ/k) can be considered as being independent of Λ/k, such a correction term in R(k) − R(0) can arise only from the corresponding correction term in G(k), in accordance with the scaling analysis of the diagrams in [6]. Hence, this assumption leads to the conclusion that G(k) must contain a correction with the exponent ω1 = η to satisfy (18 ). Such a correction exponent, i.e., ω1 = 1/4 in two dimensions, is not confirmed by our actual MC estimation in section 3 . It already indicates that the assumption considered here is not valid for the correction terms. The formal reason for this discrepancy could be the fact that the other contributions, apart from those of the region qℓ ~ k, are important.
This discrepancy can be easily resolved, including taking the analytical background contribution into consideration. It shows up as an additive ~ k2 analytical term in R(k) − R(0), which comes from the whole integration region qℓ ≤ Λ. As we have tested, considering only the simplest skeleton diagrams, this additive contribution can compensate the term ck2 in (18 ). In this case, no correction with the exponent ω1 = η appears in G(k).
An approximate qualitative analysis can be performed, including the analytical background contribution in addition to the contributions of the region qℓ ~ k. The latter contributions can be evaluated by formally setting ${\rm{\Lambda }}={ \mathcal C }k$, where ${ \mathcal C }$ is a positive constant. It reduces to the formal setting ${{\rm{\Psi }}}_{i}({\rm{\Lambda }}/k)\to {{\rm{\Psi }}}_{i}({ \mathcal C })$ in (19 ). The analytical background contribution shows up as an additional term of the form $\tilde{c}{k}^{2}+o\left({k}^{2}\right)$, where $\tilde{c}$ is a constant. The expected compensation of the term ck2 in (18 ) takes place at $\tilde{c}=-c$.
The amplitude a in G(k) = ak−λ at k → 0 is not uniquely defined from the asymptotic solution of (18 ), if only the leading terms are taken into account. Namely, setting G(k) = ak−λ, we have (2a)−1kλ in the left hand side of (18 ) and ${(2a)}^{-1}{k}^{\lambda }\,{\widetilde{{\rm{\Psi }}}}_{0}({\rm{\Lambda }}/k,\lambda )={(2a)}^{-1}{k}^{\lambda }\,{\widetilde{{\rm{\Psi }}}}_{0}({ \mathcal C },\lambda )$ in the right hand side of this equation, where ${\widetilde{{\rm{\Psi }}}}_{0}=2a{{\rm{\Psi }}}_{0}$ is the normalized scaling function, which is independent of a. It follows from the diagrammatic analysis in [6] with the inclusion of only the leading terms. Hence, the exponent λ is obtained from the condition ${\widetilde{{\rm{\Psi }}}}_{0}({ \mathcal C },\lambda )=1$, whereas the amplitude a remains uncertain.
An approximate estimation of the coefficient $\tilde{c}$ is possible for the simplest skeleton diagrams (including only the first expansion term in equation (29) of [6]), at least. It turns out that this coefficient depends on the amplitude a in such an estimation, i.e., we have $\tilde{c}=\tilde{c}(a)$. Since the amplitude a is not uniquely determined yet, we can use it as a free parameter to find a solution satisfying the expected relation $\tilde{c}=-c$ at a certain value of a. The absence of the correction with the exponent ω1 = η in G(k) implies that this is the physically meaningful solution. In this case, ω = 2λ − d = 4 − d − 2η shows up as the leading correction-to-scaling exponent in our approximation. It follows on from the scaling analysis of the diagrams in [6], where two independent correction exponents, i.e., η and 2λ − d, have been found. Only the second one survives at the condition $\tilde{c}=-c$.
In analogy with the analysis in section 4 , the problem can appear to be unexpectedly complex, and the dependence of the scaling functions on Λ/k may also influence the results. Therefore, we consider the obtained relation between η and ω as an approximation, i.e.,
$\begin{eqnarray}\omega \approx 4-d-2\eta \qquad {\rm{for}}\quad d\lt 4,\end{eqnarray}$
resulting from an approximate evaluation of R(k) − R(0) at a finite value of ${ \mathcal C }$.Although our approximation scheme, eventually, does not allow us to approach the exact solution of (18 ) due to the problems discussed, (20 ) turns out to be a valid estimate. Indeed, it gives an asymptotically correct result at ϵ = 4 − d → 0, as well as at N → ∞, where ω ≈ ϵ. It gives ω ≈ 0.928 for the 3D Ising model (where η ≈ 0.036), which is comparable with numerical estimates, usually providing ω around 0.8, and is probably not worse than the local potential approximation, giving ω ≈ 0.65 (e.g., see references in [33]). The approximation (20 ) gives ω ≈ 1.5 in two dimensions in a surprisingly good agreement with our actual best MC estimate, ω = 1.509(14), which is valid if the leading non-analytical correction to scaling has the pure power-law form. So, an accurate agreement is, indeed, surprising since (20 ) is just an approximation, which is not very accurate in the three dimensions. Allowing for logarithmic corrections, the correct ω value might be 4/3, as discussed throughout our paper. In this case, the value 1.5 of ω at d = 2 provided by (20 ) appears to be somewhat overestimated, just as in the 3D case.
The discussion above reveals essential challenges in the analysis of the diagrammatic equations derived in [6]. Nevertheless, this GFD method can be useful in some cases. Particularly, it is suited for the analysis of the large N limit, where asymptotically correct results are provided by relatively simple equations of this approach, containing only the first diagram in expansion (29) of [6]. The detailed analysis of this case goes beyond the scope of this paper. Nonetheless, we can mention the fact that the known asymptotic result for η at large N and 2 < d < 4 [36], i.e.,
$\begin{eqnarray}\eta =\frac{2}{N}\ \frac{\sin (\pi d/2)\,{\rm{\Gamma }}(d-1)\,(1-[4/d])}{\pi {\left[{\rm{\Gamma }}(d/2)\right]}^{2}},\end{eqnarray}$
is easily recovered from these GFD equations. Therefore, it is also very interesting to look at what these equations give for the Goldstone mode singularity at large N.6. Summary and discussion
Based on our MC analysis, the following three theoretical possibilities concerning the asymptotic behavior of the leading non-analytical correction to scaling in the 2D φ4 model can be considered:
(i) In view of our best MC estimates (each from its own data set) valid for ∝ L−ω scaling of the non-analytical correction term, i.e., ω = 1.509(14), ω = 1.546(30), ω = 1.540(69), ω = 1.567(58) and ω = 1.61(44), the correction-to-scaling exponent ω is close to 1.5 if this scaling has, indeed, a pure power-law form. The most accurate estimate ω = 1.509(14) among these ones suggests that ω could be just 1.5, but we do not stress on this value, allowing for a slightly larger value as very probable. This concept is plausible from the point of view that the power-law scaling is the usual one. The only problem is that such values of ω are currently not confirmed by any exact result.
(ii) Looking for consistency with some exact result, we have found that ω is consistent with 4/3, provided that the ∝ L−ω scaling is modified by the logarithmic correction factor $1/\mathrm{ln}L$. The value 4/3 has been reported in [28] as the value of two coinciding correction-to-scaling exponents θ and $\theta ^{\prime} $, describing the fractal geometry of the critical Potts clusters in the case of the Ising model (q = 2) in two dimensions. We have considered the coincidence of these exponents as the reason for possible logarithmic correction. This conception seems to be very plausible from the point of view that it establishes the consistency with the exact exponent 4/3 found in [28]. However, we still have some concerns about its validity, since it is not rigorously clear whether or not the exponents θ and $\theta ^{\prime} $ are applicable to other quantities apart from those related to the fractal geometry of the critical Potts clusters. This is a relevant question from the point of view of the CFT discussed in [27], since the percolation problem of [28] is a nonunitary extension of the theory, and no correction exponent 4/3 has been found in the unitary φ4 theory, suggesting ω = 2. Nevertheless, we still consider options with ω ≠ 2 because the observed scaling of various quantities, e.g., ${\widetilde{\beta }}_{c}(L)$ at U = U* (accurately described by ω = 1.509(14) at κ = 0 in (
(iii) Considering logarithmic corrections, one more possibility has been revealed. Namely, the $\propto {L}^{-7/4}\mathrm{ln}L$ scaling with ω = 7/4 = 1.75 appears to be pretty well consistent with the data. This concept can be seen as plausible because the ω = 1.75 version is supported by the findings in [7], where this value of ω is considered to be exact. However, there are some concerns about the validity of this conception, too. The basic problem is the absence of any theoretical argument for the existence of the logarithmic correction in this case, noting that the data cannot be acceptably fit with ω = 1.75 without such a correction. A positive aspect, however, is that the logarithmic correction $\mathrm{ln}L$ is more usual than the $1/\mathrm{ln}L$ correction, and it really exists in many cases. A real support for ω = 1.75 comes from the ε-expansion in [7], yielding ω = 1.71(10), rather than from that suggested in [7]'s reference (our [27]), claiming ω = 2. The accuracy of the ε-expansion at ε = 2, however, is questionable.
The revealed discrepancies with our earlier expectations have been resolved, reconsidering the scaling assumptions of [11] concerning the singularity of specific heat and the two-point correlation function G(k) in the vicinity of the critical point. These scaling assumptions are replaced with more general (more flexible) ones in section 4 . This renewed scaling consideration is also crucial for the GFD analysis in [6]. The corrected GFD analysis is proposed in section 5 . It does not allow us to predict the possible exact values of the critical exponents, suggested earlier in [6]. However, it still allows us to propose some approximation (20 ), relating to the critical exponents ω and η. It gives ω ≈ 1.5 for the 2D φ4 model. Despite the challenges in the general GFD analysis, we see a perspective in its application to the large N limit. It allows us to easily recover the known result (21 ). Moreover, it can be further applied to the analysis of the Goldstone mode singularity at large N.