Communications in Theoretical Physics

Editor's suggestion：Discrete Boltzmann Method with Maxwell-Type Boundary Condition for Slip Flow

近年来，随着微机电系统（MEMS）和纳米技术的发展，流体在微纳尺度的流动特性逐渐进入人们的关注热点。因为人们发现，在微纳尺度通道内，气体的流动和传热特性与传统宏观尺度上的认识存在较大差异。另外，在航空航天领域，人们也发现随着飞行器高度的提升，空气逐渐变得更加稀薄，传统Navier-Stokes方程组预测的结果也逐渐偏离实际情形。在研究这类问题时, 经常用到的一个流体力学无量纲数叫做Knudsen数, 它定义为分子平均间距与系统内某一特征尺度之比,表征流体系统相对的连续程度或离散程度。因为分子、分母同除以一个速度, 就成为两个时间之比,所以Knudsen数也经常表示为系统的热力学弛豫时间与系统内对应的流动模式特征时间之比，而热力学弛豫时间可以作为系统偏离热力学平衡程度的一种量度。这样，Knudsen数又常用来描述在关注的流动模式下，流体系统的热力学非平衡程度。钱学森先生在研究稀薄气体动力学时最早提出，可以根据Knudsen数从小到大将流动行为划分成连续流、滑移流、过渡流和自由分子流。

当系统特征尺度固定时，Knudsen数增大对应气体越来越稀薄；当流体分子平均间距固定时，Knudsen数增加对应关注的特征尺度越来越小。传统的流体力学理论是基于连续性介质假设而建立起来的，即假设分子的平均间距远小于系统的特征尺度，以至于Knudsen数小到可以忽略的程度。传统流体力学基本方程组Navier- Stokes（NS）方程组中采用线性本构关系（牛顿粘性定律和傅里叶导热定律），这其实又隐含了近（热力学）平衡假设。Navier- Stokes方程组中粘性应力项和热传导项是系统偏离热力学平衡态的粗略反映，但只有当系统偏离平衡态不太远的时候才适用。

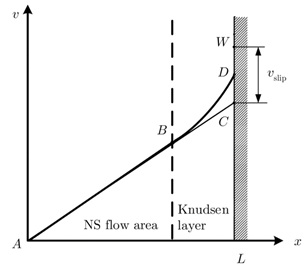
随着Knudsen的增加，连续性假设的适用性逐渐降低，非平衡效应首先在边界附近体现出来。在滑移流区，远离壁面的区域流动特性尚可以用连续的NS方程来描述，而在壁面处速度和温度分布会存在不连续性，也就是通常所说的速度滑移和温度跳变；同时，在靠近壁面附近约几个分子平均自由程的宽度内存在一个Knudsen层，在Knudsen层内速度和温度部分不再服从NS方程中的线性的牛顿粘性定律和傅里叶导热定律，而是呈现出一种非线性分布的曲线，一般称为Knudsen层曲线，如图1所示。由于在壁面附近存在着显著的非平衡效应，传统的NS方程面临挑战。

图1: 速度滑移和Knudsen层示意图

非平衡统计物理学的Boltzmann方程原则上适用于理想气体模型下任意Knudsen数流体行为的描述，在不同程度的非平衡流动描述能力方面具有自适应性。然而由于Boltzmann方程的高维特性和复杂的碰撞项，在实际计算中往往难以直接使用，所以众多实际问题的模拟研究要求对Boltzmann方程进行合理简化，即粗粒化物理建模。离散Boltzmann方法（DBM）是近年来许爱国研究员课题组在偏微分方程的格子 Boltzmann解法的基础上，对建模规则进行更加严格的物理约束，增加非平衡信息提取、分析功能发展起来的。DBM的目标不再是求解已有偏微分方程(组)，而是一种复杂流动非平衡行为的粗粒化物理建模（根据具体问题研究需求，有所保，有所丢）。DBM在原始Boltzmann方程的基础上做了两步重要的粗粒化物理建模（简化碰撞算符和离散粒子速度空间），使物理模型得到了极大的简化，显著提高了运算的效率，同时在非平衡流动特征描述方面具有超越NS的物理功能。目前，DBM已经在一系列复杂流动问题的非平衡特性研究方面获得了广泛应用。例如，在高速可压缩流动、多相流和非平衡相变、燃烧与爆轰、流体不稳定性等领域均带来一系列新的发现或认识。近期，许爱国研究员课题组(张玉东，许爱国，张广财，陈志华)发展了滑移流系统的DBM，该模型采用了Maxwell类型的速度反射边界，通过在气体分子反射模型中引入切向动量协调系数，并将其成功应用于离散速度模型中。基于新模型可以准确捕捉到不同Knudsen数和切向通量协调系数下的速度滑移和Knudsen层曲线（见图2和3），这一工作为DBM在更深层次、更加复杂的非平衡流动研究方面奠定了较好了基础。

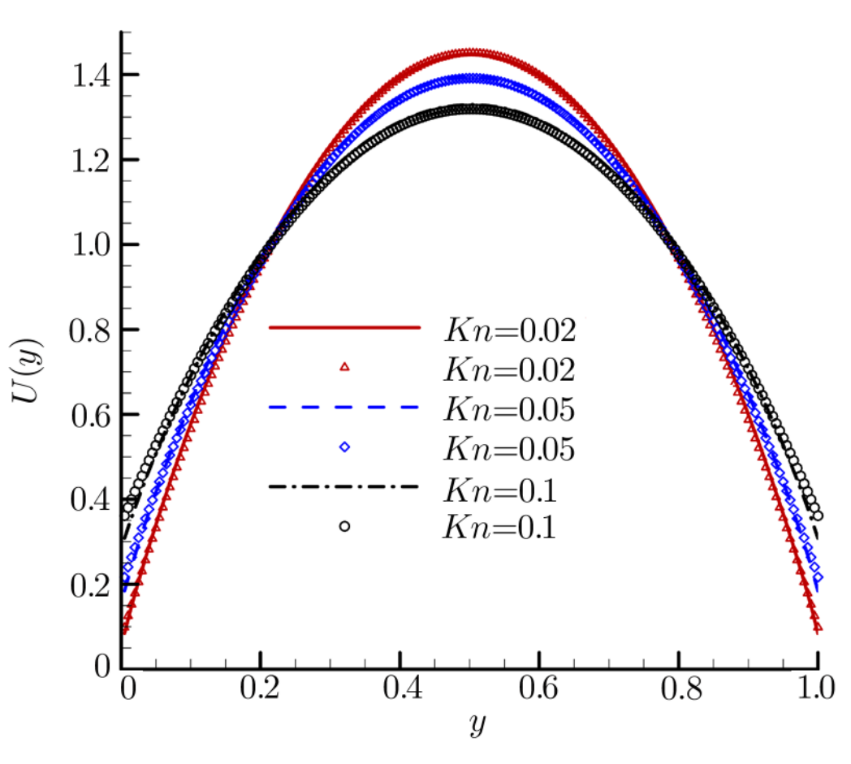
图 2不同Knudsen数下的速度滑移特性（符号为DBM结果，线型为滑移解析解）

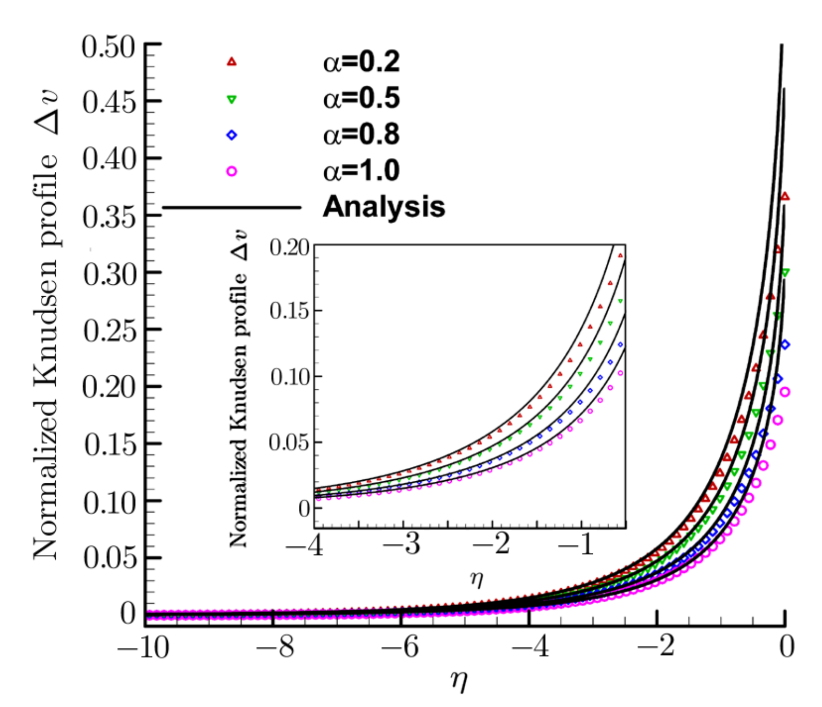
图3 不同切向动量协调系数下的Knudsen层曲线分布（符号为DBM模拟结果，实线为解析解）

该工作得到国家自然科学基金(批准号：11475028、11772064、11502117)和科学挑战计划（批准号：JCKY2016212A501）的资助。