A Renormalized-Hamiltonian-Flow Approach to Eigenenergies and Eigenfunctions *

Wen-Ge Wang

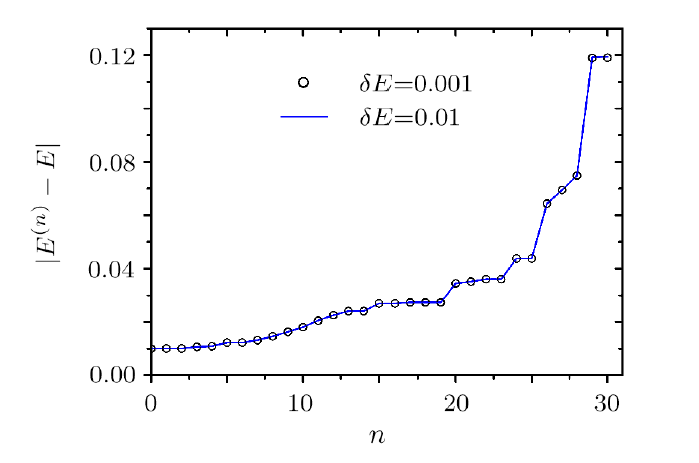
Fig. 1 Variation of $|E^{(n)}-E|$ with $n$, for the parameters $N=1000, b=100$, and $\lambda =10$, where $E^{(n)}$ is the eigenenergy of $H^{(n)}_E$ which is the closest to $E$. The value of $E$ has a little deviation from an arbitrarily chosen exact eigenenergy $E_{\alpha^{(0)}}$ of the original Hamiltonian $H^{(0)}$. For the solid curve, $\delta E =|E-E_{\alpha^{(0)}}|=0.01$. At each step of the flow, an arbitrarily chosen set of 30 basis states with successive labelling are decimated. The value of $|E^{(n)}-E|$ increases with $n$, implying that $E_{\alpha ^{(0)}}$ is an unstable fixed point. The circles represent $|E^{(n)}-E|/10$ for $\delta E =0.001$. The agreement of the solid curve and the circles show that for these small values of $\delta E$, $|E^{(n)}-E|$ is in the linear region of $\delta E$.