A Renormalized-Hamiltonian-Flow Approach to Eigenenergies and Eigenfunctions *

Wen-Ge Wang

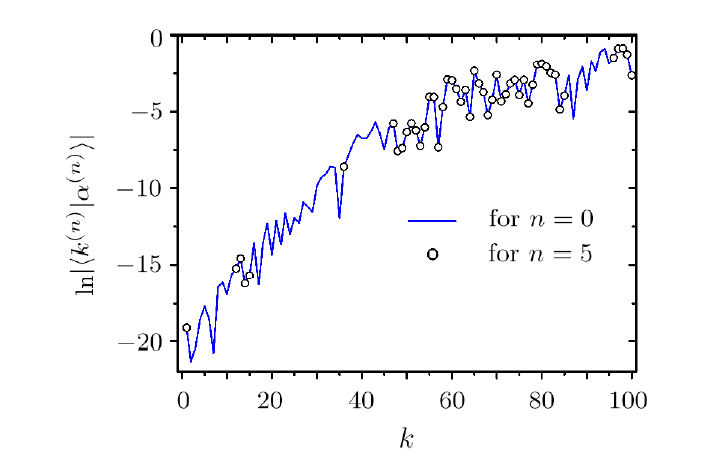
Fig. 3 Values of the components $|\langle k^{(n)}|\alpha^{(n)}\rangle |$ for $n=0$ and 5 in a renormalized Hamiltonian flow of $H^{(n)}_E$. The original Hamiltonian is a realization of the Hamiltonian matrix in the WBRM model with parameters $N=100$, $b=4$, and $\lambda =10$. In the construction of the renormalized Hamiltonians, $E=E_{\alpha^{(0)}}$ and 10 basis states are decimated at each step of the flow. $|\alpha^{(0)}\rangle $ and $|\alpha^{(5)}\rangle $ are eigenstates of $H^{(0)}$ and $H^{(5)}_E$, respectively, with the same eigenenergy $E_{\alpha^{(0)}}$. The two eigenfunctions agree well, as predicted in Eq. (23).