Perfect Optical Nonreciprocity with Mechanical Driving in a Three-Mode Optomechanical System *

Li-Hua Zhao,Xian-Li Li,He-Lin Lu,Xue-Dong Tian

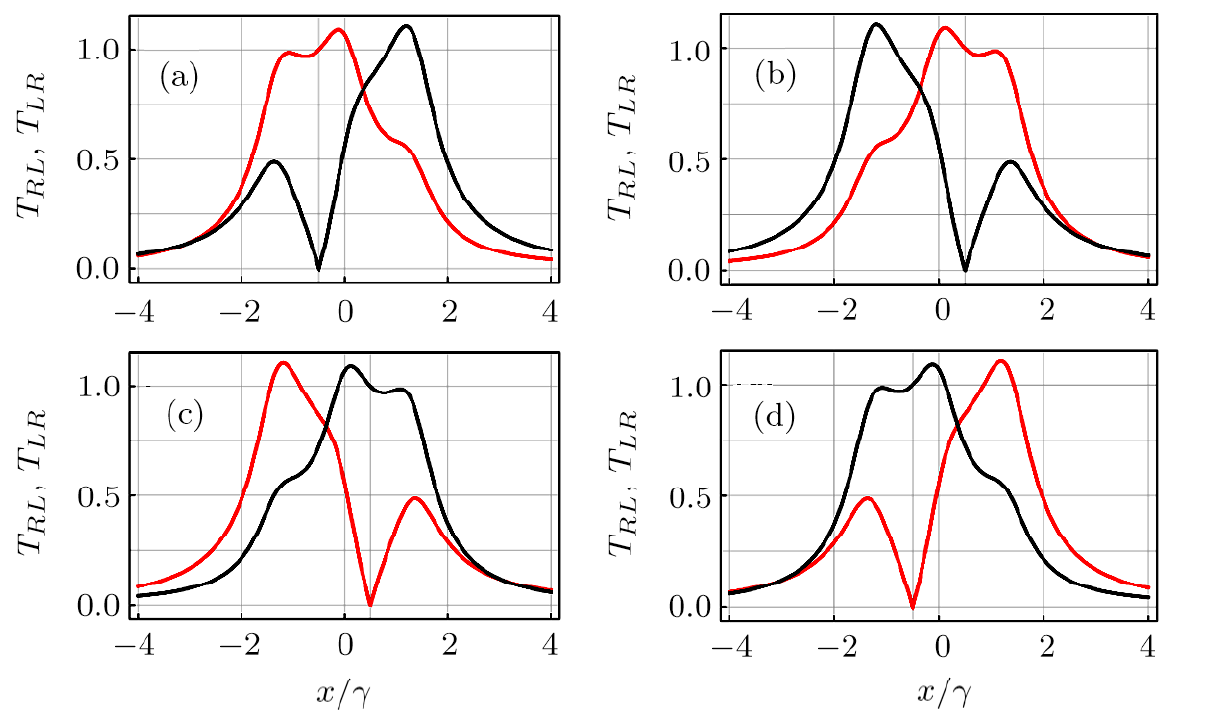
Fig. 4 (Color online) Transmission amplitudes $T_{LR}$ (red line) and $T_{RL}$ (black line) are plotted vs.\ normalized detuning $x/\gamma$ for differentmechanical driving phase and couplings $G_{i}$: (a) $\phi={\pi}/{4}$, $G_{1}=\gamma\sqrt[3]{\csc\phi}$, and $G_{2}={\gamma\csc\phi}/{2}$ according to Eq. (14), (b) $\phi={3\pi}/{4}$,$G_{1}=\gamma\sqrt[3]{\csc\phi}$, and $G_{2}={\gamma\csc\phi}/{2}$ according to Eq. (14), (c) $\phi=-{\pi}/{4}$, $G_{1}=-{\gamma\csc\phi}/{2}$, and $G_{2}=-\gamma\sqrt[3]{\csc\phi}$ according to Eq. (15), (d) $\phi=-{3\pi}/{4}$, $G_{1}=-{\gamma\csc\phi}/{2}$, and $G_{2}=-\gamma\sqrt[3]{\csc\phi}$ according to Eq. (15). The other parameter: $\kappa=\gamma$.