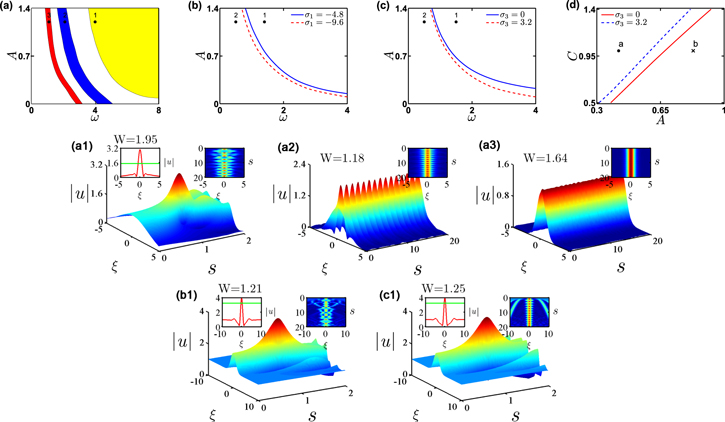
Figure 3. Choosing far-detuned optical lattice field $| v{| }^{2}={{\rm{e}}}^{\left(-\tfrac{{\xi }^{2}}{25}\right)}$ in equation (6). (a) The phase transition regions of nonlinear modes for equation (6) as the function of the initial amplitude A and width w when taking C = 0. (b) The phase transition curves of the rogue wave for equation (6) as the function of the initial amplitude A and width w when taking C = 1. Here, σ1 = −4.8 and −9.6. (c) The phase transition curves of the rogue wave for equation (6) as the function of the initial amplitude A and width w when taking C = 1. Here, σ3 = 0 and 3.2. (d) The phase transition curves of the rogue wave for equation (6) as the function of the initial amplitude A and the background height C with σ3 = 0 (red solid line) and σ3 = 3.2 (blue dotted line). Here, ω = 1.5. (a1)–(a3) The evolution results of the initial incident pulse (8) with these parameters corresponding to the black points 1–3 in figure 3(a). Here, A = 1.2, ω = 4, 2.1, and 1.1, respectively. The FWHM of (a1)–(a3) are W = 1.95, 1.18, and 1.64, respectively. (b1) The evolution results of the initial incident pulse (8) with these parameters corresponding to the black point 1 in figure 3(b). Here, A = 1.2 and ω = 1.4. FWHM of (b1) is W = 1.21. (c1) The evolution results of the initial incident pulse (8) with these parameters corresponding to the black point 1 in figure 3(c). Here, A = 1.2 and ω = 1.5. FWHM of (c1) is W = 1.25.
|