Variational theory for the ground state and collective excitations of an elongated dipolar condensate

P Blair Blakie,D Baillie,Sukla Pal

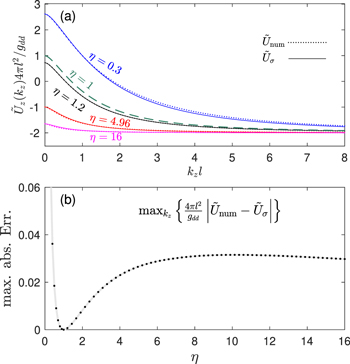
Figure 2. (a) Comparison of the (dotted lines) analytic result (18) to (solid lines) numerically calculated ${\tilde{U}}_{\mathrm{num}}$ (obtained by numerically evaluating equation (13) using $\chi \to {\chi }_{\sigma })$ for the effective k-space kernel. Results shown for several values of η and for gs = 0. The exact result for η = 1 is also shown (dashed line). (b) The maximum absolute error of the approximation ${\tilde{U}}_{\sigma }$ compared to the ${\tilde{U}}_{\mathrm{num}}$ over the kz-range shown in (a), (in units of ${g}_{{dd}}/4\pi {l}^{2}$).