Quantum dynamics of electric-dipole coupled defect centers in solids

Feng Tang,Lei-Ming Zhou,Nan Zhao

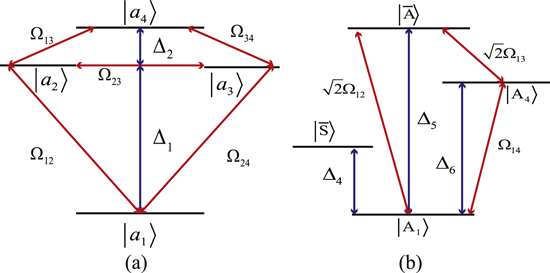
Figure 5. (a) Couplings among antisymmetry states $\{| {a}_{i}\}$. The blue lines denote the energy-level difference between two antisymmetry states: ${\bigtriangleup }_{1}={\omega }_{p}+{{\rm{\Omega }}}_{11}-{{\rm{\Omega }}}_{22}$ and ${\bigtriangleup }_{2}={\omega }_{p}+{{\rm{\Omega }}}_{33}-{{\rm{\Omega }}}_{44}$. The red lines denote the coherent coupling strength between corresponding energy levels. In this figure, the coupling between $| {a}_{1}\rangle $ and $| {a}_{4}\rangle $ is not drawn because the energy difference $\bigtriangleup ={\bigtriangleup }_{1}+{\bigtriangleup }_{2}$ is much larger than the coupling strength Ω14 between them ($\bigtriangleup \gg {{\rm{\Omega }}}_{14}$). (b) Couplings in the new basis $\{| \bar{A}\rangle ,| \bar{S}\rangle ,| {A}_{1}\rangle ,| {A}_{4}\rangle \}$. Blue lines denote the energy difference between corresponding states. ${\bigtriangleup }_{4}={\omega }_{p}+{{\rm{\Omega }}}_{11}+{{\rm{\Omega }}}_{23}-{{\rm{\Omega }}}_{22}$. ${\bigtriangleup }_{5}={\omega }_{p}+{{\rm{\Omega }}}_{11}-{{\rm{\Omega }}}_{23}-{{\rm{\Omega }}}_{22}$. ${\bigtriangleup }_{6}=2{\omega }_{p}+{{\rm{\Omega }}}_{33}-{{\rm{\Omega }}}_{22}$. The red lines specify the coherent coupling strength in the new basis. $| \bar{S}\rangle $ is totally decoupled from other energy levels.