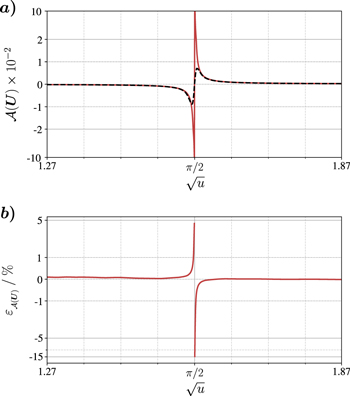
Figure 4. (a): Predicted scattering lengths ${ \mathcal A }({\boldsymbol{U}})$ for potential wells with depths u with ${ \mathcal A }$ as given in equation (9) (solid red line) and, respectively, with an ensemble ${ \mathcal A }$ of ten MLPs ${{ \mathcal A }}_{i}$ that are trained to directly predict a0 (dashed black line). (b): Relative errors ${\varepsilon }_{{}_{{ \mathcal A }({\boldsymbol{U}})}}$ of predicted scattering lengths ${ \mathcal A }({\boldsymbol{U}})$ for potential wells with depths u. The $| {\varepsilon }_{{}_{{ \mathcal A }({\boldsymbol{U}})}}| $ only take values between 1% and 15% in close vicinity of the unitary limit and become negligibly small elsewhere.
|