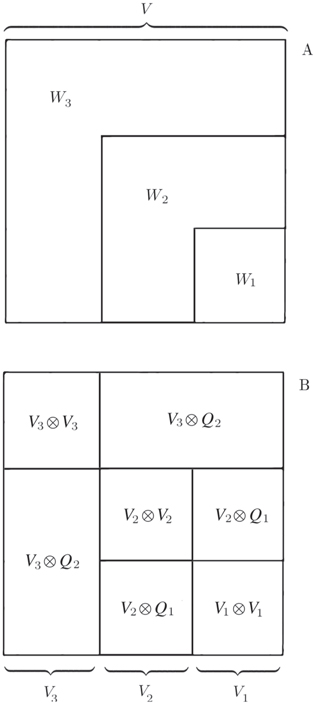
Figure 1. Figure A shows the partition of $V\otimes V$ following that of V for L 3. The edges set is split into subsets Wℓ containing all the edges with both ends in Qℓ minus those with both ends in ${Q}_{{\ell }-1}$. The bottom figure (B) is intended to explain the structure of Wℓ in terms of layers of spins: ${V}_{{\ell }}\otimes {V}_{{\ell }}$ contain the edges between the spins of Vℓ, while ${V}_{{\ell }}\otimes {Q}_{{\ell }-1}$ and ${Q}_{{\ell }-1}\otimes {V}_{{\ell }}$ contain the edges that make the interface between the layer Vℓ and the rest of the system.
|