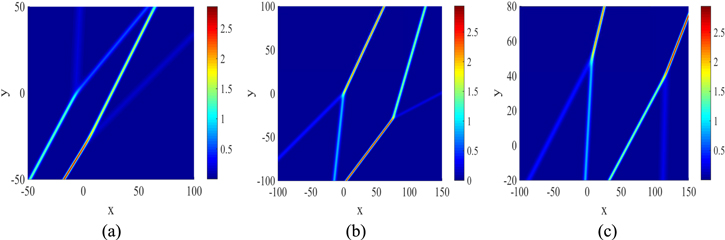
Figure 3. Three different types of interactions of two 2-resonance Y-type solitons at t = 0, described by equation (10) with: (a) ${k}_{1}=-\frac{3}{2},$ ${k}_{2}=-\frac{5}{11},$ ${k}_{3}=\frac{4}{3},$ ${k}_{4}=\frac{1}{2},$ ${p}_{1}=\frac{7}{6},$ ${p}_{2}=\frac{136435}{95832}+\frac{215\sqrt{93}}{2904},$ ${p}_{3}=-\frac{10}{9},$ ${p}_{4}=-\frac{35}{72}+\frac{5\sqrt{42}}{72},$ φ1 = 30, φ2 = − 20, φ3 = 0, φ4 = 0; (b) ${k}_{1}=\frac{7}{5},$ k2 = 1, ${k}_{3}=-\frac{1}{2},$ ${k}_{4}=\frac{3}{4},$ ${p}_{1}=-\frac{7}{5},$ ${p}_{2}=-\frac{22}{25}+\frac{3\sqrt{17}}{25},$ ${p}_{3}=\frac{2}{3},$ ${p}_{4}=-\frac{31}{16}-\frac{15\sqrt{61}}{64},$ φ1 = − 140, φ2 = − 80, φ3 = 0, φ4 = 0; (c) ${k}_{1}=\frac{7}{5},$ k2 = 1, ${k}_{3}=-\frac{1}{2},$ ${k}_{4}=\frac{3}{4},$ ${p}_{1}=-\frac{7}{5},$ ${p}_{2}=-\frac{22}{25}-\frac{3\sqrt{17}}{25},$ ${p}_{3}=\frac{2}{3},$ ${p}_{4}=-\frac{31}{16}-\frac{15\sqrt{61}}{64},$ φ1 = − 100, φ2 = − 60, φ3 = − 30, φ4 = 0.
|