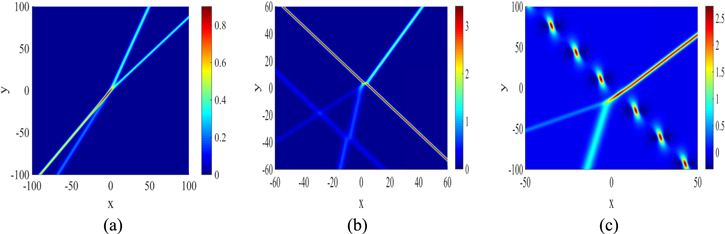
Figure 4. Some solutions to equation (3) at t = 0: (a) a double openings of resonance Y-type soliton described by equation (4) with ${k}_{1}=\frac{1}{4},$ ${k}_{2}=-\frac{7}{8},$ ${k}_{3}=-\frac{4}{19},$ ${p}_{1}=-\frac{7}{12},$ ${p}_{2}=\frac{581}{192}+\frac{63\ \sqrt{445}}{512},$ ${p}_{3}=-\frac{35\ \sqrt{445}}{2888}+\frac{86219}{164616},$ φ1 = 0, φ2 = 0, φ3 = 0; (b) an interaction between a resonance Y-type soliton and a line wave molecule described by equation (4) with ${k}_{1}=\frac{16}{11},$ ${k}_{2}=\frac{5}{9},$ ${k}_{3}=\frac{2}{3},$ ${k}_{4}=-\frac{\sqrt{41}}{3},$ p1 = − 1, ${p}_{2}=-\frac{660095}{1411344}-\frac{445\ \sqrt{921}}{39204},$ ${p}_{3}=\frac{2}{3},$ ${p}_{4}=-\frac{\sqrt{41}}{3},$ φ1 = 0, φ2 = 0, φ3 = 30, φ4 = 10; (c) an interaction between a resonance Y-type soliton and a breather wave described by equation (4) with ${k}_{1}=-\frac{1}{2},$ ${k}_{2}=\frac{3}{4},$ ${k}_{3}=\frac{2}{7}-\frac{2i}{7},$ ${k}_{4}=\frac{2}{7}+\frac{2i}{7},$ ${p}_{1}=-\frac{2}{3},$ ${p}_{2}=-\frac{31}{16}+\frac{15\ \sqrt{61}}{64},$ ${p}_{3}=\frac{1}{8}+\frac{i}{15},$ ${p}_{4}=\frac{1}{8}-\frac{i}{15},$ φ1 = 10, φ2 = 0, φ3 = 0, φ4 = 0.
|