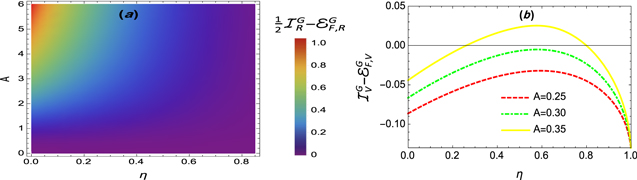
Figure 2. (a): $\tfrac{1}{2}{{ \mathcal I }}_{R}^{G}-{{ \mathcal E }}_{F,R}^{G}$ and (b): ${{ \mathcal I }}_{V}^{G}-{{ \mathcal E }}_{F,V}^{G}$ versus the parameters A and η for κ = 1. (a) shows that the constraint $(1/2){{ \mathcal I }}_{\alpha }^{G}\geqslant {{ \mathcal E }}_{F,\alpha }^{G}$ is satisfied via the Rényi-2 entropy (i.e. α = 2), in contrast, it is largely violated—in (b)—via the von Neumann entropy (i.e. α = 1), where even ${{ \mathcal E }}_{F,V}^{G}\geqslant {{ \mathcal I }}_{V}^{G}$ may happen, which consolidates the Hayden conjecture [40], in addition, undermines the interpretation of the von Neumann EoF ${{ \mathcal E }}_{F,V}$ as just a fraction of the total correlations.
|