The Lindblad and Redfield forms derived from the Born–Markov master equation without secular approximation and their applications
|
The Lindblad and Redfield forms derived from the Born–Markov master equation without secular approximation and their applications |
| Chang-Yao Liao,Xian-Ting Liang |
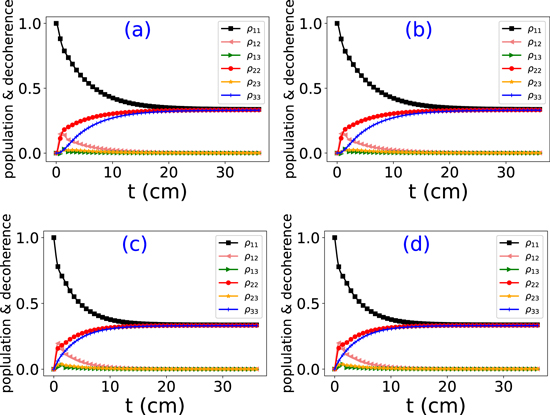
| Figure 1. The evolution of the reduced density matrix for a three-level quantum system obtained using the non-secular equations (Lindblad and Redfield forms) with ${{\rm{\Gamma }}}_{\alpha \beta }^{(2)}({\omega }_{{mn}})$ (a) and ${{\rm{\Gamma }}}_{\alpha \beta }^{(1)}({\omega }_{{mn}})$ (b); secular equations with ${{\rm{\Gamma }}}_{\alpha \beta }^{(2)}({\omega }_{{mn}})$ (c), and ${{\rm{\Gamma }}}_{\alpha \beta }^{(1)}({\omega }_{{mn}})$ (d). Here, we set the the environmental spectral density function to the Drude form, with η = 0.125, Ω = 100.0 cm−1, T = 300 K. The initial state is set to ρ(0) = ∣1⟩⟨1∣. In equation ( |

|