Self-consistent tomography of temporally correlated errors
|
Self-consistent tomography of temporally correlated errors |
| Mingxia Huo,Ying Li |
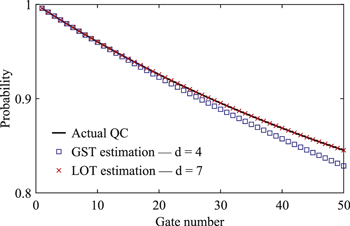
| Figure 2. Probabilities in the state $\left|0\right|$ after a sequence of randomly chosen Hadamard and phase gates as functions of the gate number. We initialize the qubit in the state $\left|0\right|$, perform the random gate sequence and measure the probability in the state $\left|0\right|$. We only take into account gate sequences that the final state is $\left|0\right|$ in the case of ideal gates without error. Therefore the probability should be 1 in this case. In our simulation, we take Σ = 1 and η = 0.02. In the presence of errors, the probability in the actual quantum computation (QC) decreases with the gate number (black curve). Based on error models obtained in linear operator tomography (LOT) using MLE, we can estimate the decreasing probability, and the results are plotted. We can find the that the error model with d = 7 (red crosses) fits the actual behavior of the quantum computer much more accurately than the error model with d = 4 (blue squares). When d = 4, LOT is equivalent to conventional GST. Results for the linear inversion method are similar. See appendix |

|