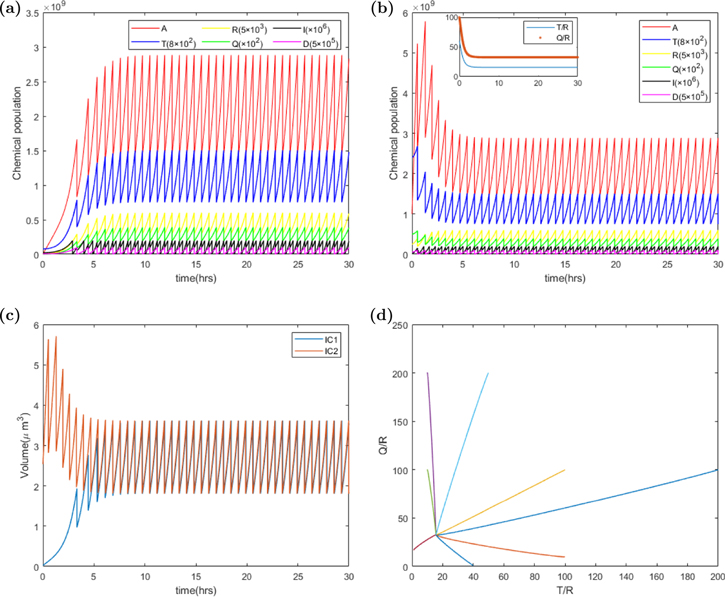
Figure 2. The deterministic trajectories of chemical populations, P, T, R, Q, I, D and volume V versus time t. Parameters of the ATRQID system are k = 3000 h−1, Σ = 3 ∗ 10−5 μm3 h−1, KD = 4 ∗ 10−12 h−1, KI = 6 ∗ 10−12 h−1, dR = dQ = dT = 0.1 h−1, Dc = 200, Ic = 200, Dr = 0, Ir = 0, and the other parameters of the model are shown in the table 1. The population values in (a) and (b) have been adjusted to make all of populations shown on the same figure by some multiplier factors. (a) The trajectory of populations versus time in a cell with the initial condition IC1: A(0) = 103, T(0) = 105, R(0) = 103, Q(0) = 104, I(0) = 20, D(0) = 10. The populations’ dynamics evolve to a steady state, and the chemical populations in the daughter cell at the birth are Ab = 1.28 ∗ 109, Tb = 8.39 ∗ 105, Rb = 5.26 ∗ 104, Qb = 1.71 ∗ 106, Ib = 88, Db = 0. The doubling time is 0.7235 h. (b) The trajectory of populations versus time in a cell with the initial condition IC2: A(0) = 109, T(0) = 3∗106, R(0) = 5∗104, Q(0) = 5∗106, I(0) = 10, D(0) = 100. The population dynamics reach a same steady state as IC1. (c) The plot of cell size versus time on the two initial conditions IC1 and IC2. (d) The 2D space of Q/R and T/R shows that the trajectories converge to the same attractor independent of initial conditions.
|