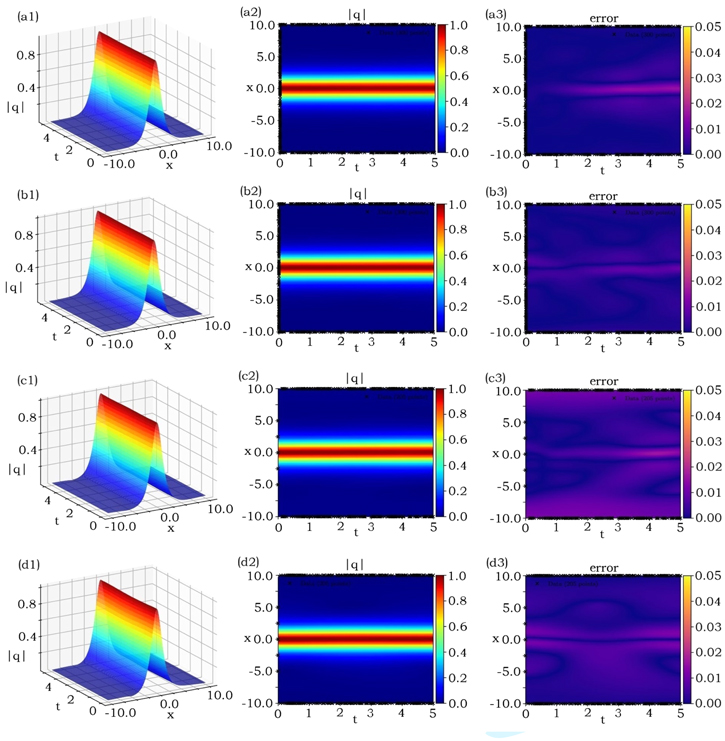
Figure 2. Data-driven bright soliton of the Hirota equation (2): (a1), (a2) and (b1), (b2) the learning solutions arising from the unpeturbated and perturbated (2%) training data related to the first case of initial data, respectively; (c1), (c2) and (d1), (d2) the learning solutions arising from the unpeturbated and perturbated (2%) training data related to the first case of initial data, respectively; (a3), (b3), (c3), (d3) the absolute values of the errors between the modules of exact and learning solutions. The relative ${{\mathbb{L}}}^{2}-$norm errors of q(x, t), u(x, t) and v(x, t), respectively, are (a1)–(a3) 9.3183 × 10−3, 5.3270 × 10−2, 3.8502 × 10−2, (b1)–(b3) 7.0707 × 10−3, 2.4057 × 10−2, 1.6464 × 10−2, (c1)–(c3) 1.8822 × 10−2, 4.9227 × 10−2, 4.0917 × 10−2, (d1)–(d3) 2.5427 × 10−2, 3.4825 × 10−2, 2.5983 × 10−2.
|