Deep learning neural networks for the third-order nonlinear Schrödinger equation: bright solitons, breathers, and rogue waves

Zijian Zhou,Zhenya Yan

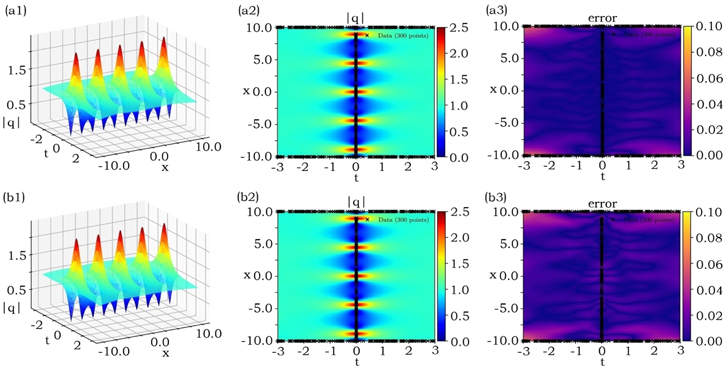
Figure 3. Learning breathers related to the AKM breather (9) of the Hirota equation (2). (a1)–(a3) The unperturbated case, (b1)–(b3) the 2% perturbated case. The relative ${{\mathbb{L}}}^{2}-$norm errors of q(x, t), u(x, t) and v(x, t), respectively, are (a1)–(a3) 1.1011 × 10−2, 3.5650 × 10−2, 5.0245 × 10−2, (b1)–(b3) 1.3458 × 10−2, 5.1326 × 10−2, 7.0242 × 10−2.