Solving forward and inverse problems of the nonlinear Schrödinger equation with the generalized ${ \mathcal P }{ \mathcal T }$-symmetric Scarf-II potential via PINN deep learning

Jiaheng Li,Biao Li

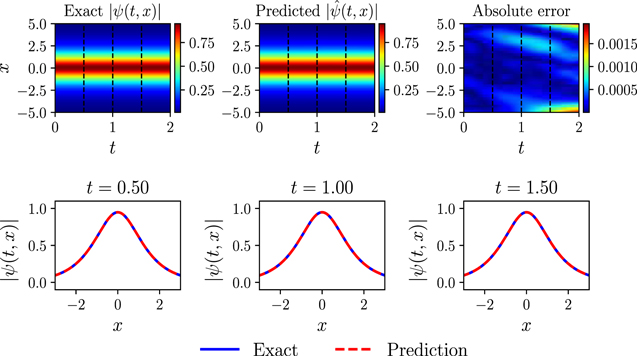
Figure 2. The defocusing NLSE with the generalized ${ \mathcal P }{ \mathcal T }$-symmetric Scarf-II potential and initial value conditions (13): Top : The magnitude of the exact solution ∣ψ(t, x)∣, predicted solution $| \hat{\psi }(t,x)| $ with ${N}_{{ \mathcal I }}=50$ random sample points with the initial value conditions and ${N}_{{ \mathcal B }}=100$ random sample points with the Dirichlet boundary conditions. ${N}_{{ \mathcal C }}=10000$ collocation points are generated by a space-filling LHS strategy, and the absolute error between the exact solutions and predicted solutions are shown, respectively. The relative ${{\mathbb{L}}}_{2}$-norm error for this case is 8.380674e-04. Bottom : Comparisons of the exact solutions and predicted solutions at the three temporal snapshots described by the three dotted black lines in the top panel corresponding to time instants t = 0.5, 1.0 and 1.5.