Solving forward and inverse problems of the nonlinear Schrödinger equation with the generalized ${ \mathcal P }{ \mathcal T }$-symmetric Scarf-II potential via PINN deep learning

Jiaheng Li,Biao Li

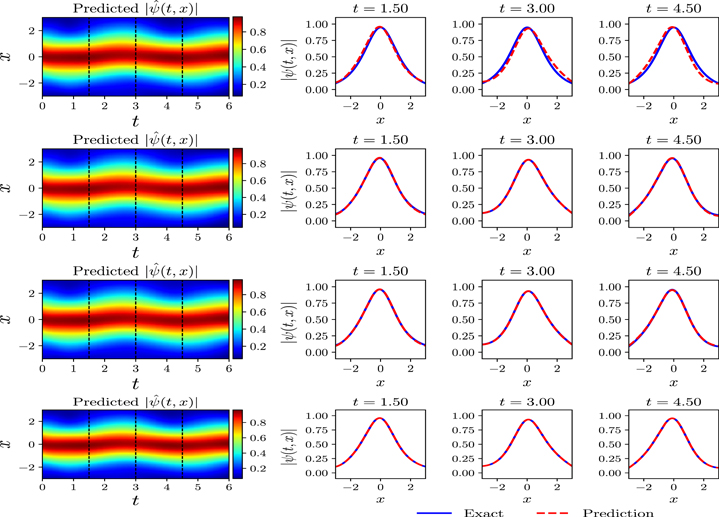
Figure 5. The optimization steps' influence on the learning ability of this complex-valued PINNs in the defocusing NLSE with the generalized ${ \mathcal P }{ \mathcal T }$-symmetric Scarf-II potential and initial boundary value conditions in Section 3.2: the deep learning results in four different optimization steps N = {20000, 30 000, 40 000, 50 000} from the first row to the last row. Left column images : the magnitude of the approximate predicted solution $| \hat{\psi }(t,x)| $ with the initial and Dirichlet boundary training data and 10 000 collocation points. Right three columns : comparisons of the exact solutions and predicted solutions at the three temporal snapshots described by the three dotted black lines in the first column corresponding to time instants t = 1.5, 3.0 and 4.5.